Представим себе такую историю.
– Интересно, что же у нас получится? – задумался Саша.
– Чем ты там занимаешься? – спросил Паша.
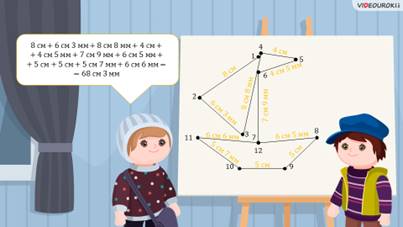
– Нам по математике задали нарисовать картинку по точкам, а потом найти сумму длин всех получившихся отрезков.
– Это интересно! Давай рисовать вместе.
– Давай! Вместе веселее.
И ребята принялись рисовать картинку.
– 1…, 2…, 3…, 4…, 5…, 6…, 7…, 8…, 9…, 10…, 11… и 12…
– Саша, смотри, у нас же получился корабль! – обрадовался Паша.
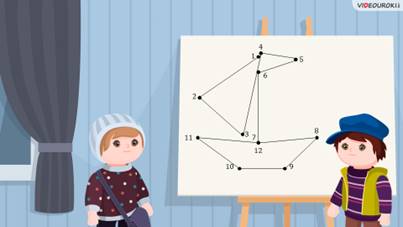
– Точно! – заметил Саша. Но нам ещё нужно вычислить сумму длин всех получившихся отрезков. Значит, будем мерить их линейкой.
– Саша, с твоей линейкой что-то не то! – отметил Паша. – Мы не сможем с помощью этой линейки измерить длины отрезков.
– Но у меня нет другой линейки. Как быть? – расстроился Саша.
– Я думаю, что Электроша будет знать, как нам быть, – предположил Паша.

– Ребята, прежде, чем я вам помогу с измерением отрезков, хочу, чтобы вы немного размялись и выполнили устные задания, – предложил Электроша.
– Давайте сверимся! Посмотрите, что у вас должно было получиться!

– Ну а теперь вернёмся к вашей проблеме, – продолжил Электроша. – Вы не можете измерить длину отрезков, потому что на вашей линейке не хватает делений.
– Что значит не хватает делений? – удивился Саша. – На моей линейке же есть деления.
– Деления-то есть, – сказал Электроша, – но посмотрите, при измерении длины второго отрезка у вас не получилось записать его длину. Вы заметили, что он длиннее, чем 6 см, но точнее вам его измерить не удалось. Другое дело будет, если мы измерим длину этого же отрезка вот такой линейкой.
– Теперь понятно, про какие деления ты говорил, – обрадовались мальчишки.
– Посмотрите, отрезок один и тот же, а результаты измерения стали точнее, – продолжил Электроша. – Как вы думаете, почему так получилось?
– Наверное, потому что на второй линейке больше отметок, – предположил Паша.
– Ты верно заметил, – сказал Электроша.
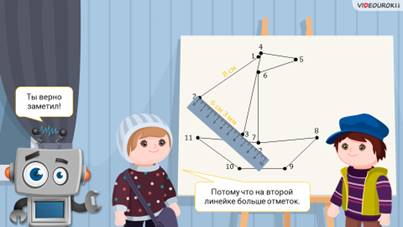
Давайте более внимательно рассмотрим эти две линейки. Посмотрите, на одной и второй линейке нанесены риски, штрихи. Все штрихи расположены на одинаковом расстоянии друг от друга. Около некоторых штрихов указаны числа. Нетрудно заметить, что все штрихи на линейках разбивают их на равные части. Эти части называют делениями.

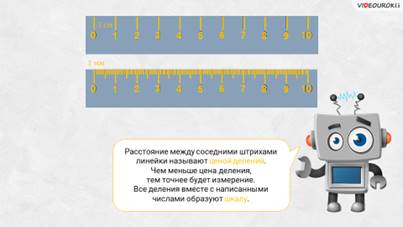
– А теперь скажите, какое расстояние между соседними штрихами первой и второй линейки, – спросил у ребят Электроша.
– Расстояние между соседними штрихами первой линейки равно 1 см, а второй – 1 мм, – ответил Саша.
– Правильно! – подтвердил Электроша. Это расстояние называют ценой деления. Чем меньше цена деления, тем точнее будет измерение. Все деления вместе с написанными числами образуют шкалу.
Кстати, «шкала» по-латыни – это лестница.
– Тогда деления – это ступеньки лестницы? – спросил Паша.
– Точно подмечено, – ответил Электроша.
– С помощью второй линейки вы можете измерить длины отрезков вашего рисунка и найти их сумму.
– Да, теперь это гораздо легче выполнить, – сказал Паша. И ребята принялись измерять отрезки.
Получили, что сумма длин всех отрезков рисунка равна 68 см 3 мм.
– В повседневной жизни вы часто встречаетесь и с другими измерительными приборами, которые тоже имеют шкалы, правда, немного другой формы, – продолжил Электроша. Может, вы сможете их назвать? – спросил он у ребят.
– Комнатный термометр, – начал Паша, – циферблат часов.
– Спидометр автомобиля, – поддержал друга Саша, – весы.

– Молодцы! – похвалил ребят Электроша. А может, вы сможете назвать цены деления перечисленных измерительных приборов?
– У комнатного термометра цена деления – 1оС, а вот у циферблата часов не знаю, как понять, какая цена деления, – расстроился Паша.

– У циферблата часов несколько шкал, каждая со своей ценой деления, – сказал Электроша. – Посмотрите, на циферблате вся окружность разделена на 12 больших делений. Одно деление соответствует одному часу. Кроме того, циферблат часов разделён на 60 маленьких делений. Одно такое маленькое деление соответствует одной минуте.

– Значит, у спидометра автомобиля цена деления шкалы 20 км/ч, а у весов цена деления 10 г? – решил уточнить Саша.


– Правильно! – похвалил Сашу Электроша. – А вы знаете, что измерительные приборы создают специально обученные люди, и их называют конструкторами? Правда, шкалы на таких измерительных приборах конечны, то есть среди отмеченных на шкале чисел всегда есть наибольшее. А вот математик с помощью своего воображения может построить бесконечную шкалу.

– Ого! – удивились ребята. – А ты можешь построить такую шкалу?
– Да! – ответил Электроша. – Сейчас мы её построим вместе.
Давайте начертим луч Ох так, чтобы он шёл слева направо. Отметим на этом луче, например, точку А. Теперь под точкой О поставим число 0, а под точкой А – число 1. Принято говорить, что точке О соответствует число 0, а точке А – число 1.
Обратите внимание, мы получили отрезок ОА, его длину будем считать равной 1.
Теперь отложим вправо от точки А отрезок, равный отрезку ОА. Получим новую точку, назовём её В, а под ней поставим число 2. Повторим этот шаг ещё раз. Получим ещё одну точку. Обозначим её буквой С, а под ней запишем число 3. Так, шаг за шагом, мы будем получать точки D, Е, F, которым будут соответствовать числа 4, 5, 6 и так далее.
– А сколько раз мы сможем проделывать эти шаги? – решили спросить ребята.
– Мы с вами знаем, что луч бесконечен, значит, мысленно этот процесс мы можем повторить бесконечное количество раз.
– Таким образом, мы с вами построили бесконечную шкалу.
– Ого! Так просто! – воскликнули ребята.
– Запомните! – продолжил Электроша. – Такую шкалу называют координатным лучом, точку О – началом отсчёта, а отрезок – ОА – единичным отрезком координатного луча. В качестве единичного отрезка можно выбрать отрезок любой длины. Часто длину единичного отрезка выбирают такой, чтобы было возможно в пределах рисунка изобразить на координатном луче необходимые натуральные числа.

– А вы сможете мне назвать то число, которое соответствует, например, точке G? – спросил у ребят Электроша.
– Число 7 соответствует точке G, – ответили мальчишки.
– Правильно! – сказал Электроша. Говорят, что число семь является координатой точки G, записывают это так…
Координата точки показывает расстояние от начала луча до этой точки, измеренное единичным отрезком. Так, например, на нашей координатной прямой точка Е имеет координату 5. Это говорит нам о том, что расстояние от начала координат до точки Е равно 5, или ещё можно сказать, что отрезок ОЕ имеет длину 5 единичных отрезков. Аналогично мы можем записать координаты остальных точек.

– А теперь, ребята, давайте посмотрим, как вы всё поняли и выполним несколько заданий.
Задание первое: назовите показания изображённых измерительных приборов.
Решение: на первом рисунке изображён комнатный термометр, который показывает температуру 31 оC. На втором рисунке изображены часы, на которых стрелки показывают время 12 ч 5 мин. И на последнем рисунке изображён спидометр автомобиля, на котором стрелка указывает скорость 90 км/ч.

Следующее задание: назовите координаты точек А, Бэ, Цэ, Дэ и отметьте на координатном луче точки.
Решение: сначала нам нужно назвать координаты точек, а для этого определим длину единичного отрезка. Видим, что от начала координат до первой известной координаты расстояние равное 30 и штрихами отмечено 3 единичных отрезка. Значит, длина единичного отрезка равна 10. А тогда координата точки А – 10, точки В – 50, точки С – 90, а точки D – 120.
Ещё нам нужно отметить на координатном луче точки с указанными координатами. Первая точка – F – имеет координату 20. Так как единичный отрезок равен 10, то отмечаем эту точку над вторым штрихом. Вторая точка – G – имеет координату 100, отмечаем её над десятым штрихом. И последняя точка – H – имеет координату 75. Значит, она будет располагаться между седьмым и восьмым штрихами.


 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 4176
4176

