Представим себе такую историю.
– Паша, а ты знаешь, что в созвездии Большой Медведицы больше звёзд, чем в созвездии Кассиопеи? – спросил Саша.
– Почему? – удивился Паша.
– Потому что в созвездии Большой Медведицы 7 звёзд, а в созвездии Кассиопеи всего лишь 5.

– Да, но это лишь видимые невооружённым глазом звёзды созвездий, – уточнил Паша. А на самом деле эти созвездия составляют гораздо больше звёзд.
Если ты посмотришь на эти созвездия в телескоп, то увидишь, что созвездие Большой Медведицы содержит около 200 звёзд, а созвездие Кассиопеи – около 150.
А на небе эти созвездия занимают огромную площадь. Так, например, площадь Большой Медведицы – 1280 квадратных градусов, а Кассиопеи – 598 квадратных градусов.

– Ого! Так много! – удивился Саша. – Только вот теперь я не могу понять, какое же из созвездий будет больше.
– Надо подумать! – сказал Паша. – А может не будем терять время и спросим у Электроши?
– Ребята, прежде чем я вам расскажу, как сравнивать большие числа, давайте немного разомнёмся и выполним устные задания, – предложил Электроша.

– Давайте сверимся! Посмотрите, что у вас должно было получиться!

– Ну а теперь поговорим о сравнении. Что значит сравнить два числа?
– Наверное, это значит определить, какое из них больше, а какое – меньше, – предположили мальчишки.

– Правильно! – похвалил ребят Электроша. Когда Саша рассказывал, что созвездие Большой Медведицы состоит из 7 звёзд, а созвездие Кассиопеи – из 5, то ему не составило труда определить, что в первом созвездии больше звёзд, чем во втором. Понятно, что число 7 больше 5.

– Числа можно сравнивать при помощи натурального ряда, – сказал Электроша. – Что называют натуральным рядом?
– Все натуральные числа, записанные в порядке возрастания, образуют натуральный ряд, – ответил Паша.

– Молодец! – похвалил Пашу Электроша. – Запомните! Из двух натуральных чисел меньшим будет то, которое в натуральном ряду стоит раньше, а большим – то, которое в натуральном ряду стоит позже.
Вот, например, число 5 в натуральном ряду стоит раньше, чем число 7, поэтому мы и говорим, что 5 меньше 7.
Результаты сравнения записывают с помощью знаков «меньше» и «больше». А сами записи называют неравенствами.

1 — самое маленькое натуральное число. Число 0 меньше любого натурального числа. Значит, число 0 и меньше 1.

Кстати, сравнивать можно одновременно и три числа. Например, сравним числа 15, 10 и 20. Что вы можете сказать об этих числах относительно их расположения в натуральном ряду? – спросил у ребят Электроша.
– Число 15 в натуральном ряду стоит позже 10, значит, число 15 больше 10, – сказал Саша.
– Но ведь в то же время число 15 в натуральном ряду стоит раньше 20, значит, число 15 меньше 20, – перебил Паша.
– Верно! – подтвердил Электроша. – Если о числе говорят, что оно меньше некоторого числа и вместе с тем больше некоторого другого числа, то тогда это утверждение записывают в виде двойного неравенства, используя при этом и знак меньше, и знак больше. Зачастую слово «двойное» не говорят, а просто называют двойное неравенство неравенством.

– Сравнивать натуральные числа можно и при помощи координатного луча, – продолжил Электроша. – Давайте начертим луч Ох и отметим на нём точки А, В, С, D, Е в любом понравившемся вам месте.
А теперь представьте себе, что наш координатный луч – это изображение линейки, на которой отмечены указанные точки. Не зная координат этих точек, вы сможете сказать, какая из них больше, а какая меньше? – спросил у ребят Электроша.
– Да, – ответили мальчишки.
– Точка А стоит левее других точек на координатном луче, значит, её координата будет меньше, – сказал Паша.
– А точка Е стоит дальше других точек на координатном луче, тогда её координата будет больше, – продолжил Саша.
– Всё правильно! – похвалил ребят Электроша. – На координатном луче точка с меньшей координатой расположена левее точки с большей координатой.
Так, например, точка А с координатой 3 лежит левее точки B с координатой 7. Значит, координата точки А меньше координаты точки B.

Запомните! На координатном луче из двух натуральных чисел меньшее число расположено левее большего.

Но не все натуральные числа удобно сравнивать, обращаясь к натуральному ряду или координатному лучу. Возьмём, к примеру, многозначные числа 200 и 150, 1280 и 598. Чтобы сравнить эти числа, нам не очень удобно будет выписывать весь натуральный ряд или чертить такой большой координатный луч. Как сравнить такие числа?
– Может, попробовать сравнить по отдельности цифры каждого числа? – предложили мальчишки.
– Мне нравится ваше предположение, – сказал Электроша. – Проще всего сравнивать многозначные числа, которые имеют разное количество цифр. Вот, например, числа 1280 и 598. Первое число содержит 4 цифры – оно четырёхзначное, второе число содержит только 3 цифры – оно трёхзначное. Какое из них будет больше?
– Четырёхзначное число больше трёхзначного, – сказал Паша, – то есть число 1280 больше 598.

– Правильно! – сказал Электроша. – Запомните! Из двух натуральных чисел, имеющих разное количество цифр, большим является то, у которого количество цифр больше.
Ну а если два многозначных числа имеют одинаковое количество цифр, то следует запомнить следующее правило: из двух натуральных чисел с одинаковым количеством цифр большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр.

– Сравните числа 200 и 150, – предложил ребятам Электроша.
– Числа 200 и 150 имеют одинаковое количество цифр, они оба трёхзначные, – сказал Паша, – но в первом числе в разряде сотен стоит цифра 2, а во втором – 1. 2 больше 1, значит, и число 200 больше 150.

– Всё правильно! – похвалил Пашу Электроша. Теперь зная, как сравнивают большие числа, вы можете сказать, какое из созвездий – Большая Медведица или Кассиопея – больше?
– Да! – воскликнули ребята. – Большая Медведица состоит из большего количества звёзд, а ещё она занимает и большую площадь на небе.

– Какие вы молодцы! – похвалил ребят Электроша. – А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.
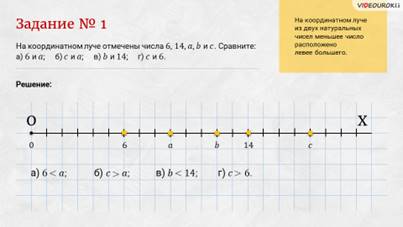
Задание первое: на координатном луче отмечены числа 6, 14, а, b и c. Сравните их.
Решение: мы знаем, что на координатном луче из двух натуральных чисел меньшее число расположено левее большего. Видим, что число 6 на координатном луче расположено левее числа а, значит, число 6 меньше а. Число с на координатном луче расположено правее числа а, значит, число с больше а. Число b на координатном луче расположено левее числа 14, значит, число b меньше 14. И последняя пара чисел. Видим, что на координатном луче число c расположено правее числа 6, значит, число c больше 6.
Следующее задание: сравните числа.
Решение: мы знаем, что из двух натуральных чисел меньшим будет то, которое в натуральном ряду стоит раньше, а большим – то, которое в натуральном ряду стоит позже. Число 4 в натуральном ряду стоит раньше числа 9, значит, 4 меньше 9.
Число 17 в натуральном ряду стоит позже 7, значит, 17 больше 7.
Следующая пара чисел: 106 и 160. Эти два числа имеют одинаковое количество цифр, они оба трёхзначные. Мы знаем, что из двух натуральных чисел с одинаковым количеством цифр большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр. В разряде сотен и у первого, и у второго числа стоит 1. Переходим к следующему разряду. Видим, что в разряде десятков в первом числе стоит 0, а во втором – 6. 0 меньше любого натурального числа, значит, и 0 меньше 6. Можем сделать вывод, что и всё число 106 меньше 160.
Сравним числа 975 и 957. Опять же видим, что эти числа имеют одинаковое количество цифр. В разряде сотен у обоих чисел стоит 9. Переходим к следующему разряду. Видим, что в разряде десятков, в первом числе, записана цифра 7, а во втором – 5. 7 больше 5. Значит, можем сделать вывод, что и всё число 975 больше числа 957.
Следующая пара чисел: 6 800 201 и 6 802 001. Оба числа семизначные, то есть имеют одинаковое количество цифр. В разряде единиц миллионов у этих чисел записана цифра 6. В следующем разряде сотен тысяч у них записана цифра 8. Переходим к следующему разряду. Видим, что в разряде десятков тысяч у обоих чисел записаны нули. А в разряде единиц тысяч в первом числе стоит цифра 0, а во втором – 2. 0 меньше 2. Значит, делаем вывод, что число 6 800 201 меньше числа 6 802 001.
И последняя пара чисел – 53 020 040 789 и 5 300 020 040 987. Видим, что эти числа состоят из разного количества цифр. Первое число одиннадцатизначное, второе – тринадцатизначное. А мы знаем, что из двух натуральных чисел, имеющих разное количество цифр, большим является то, у которого количество цифр больше. В первом числе цифр меньше, значит, и всё число меньше.


 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 3369
3369

