Самым простым видом механического движения является прямолинейное движение с постоянной по модулю и направлению скоростью:
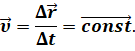
Однако не будем забывать о том, что равномерно движение — это модель реального движения. В действительности же реальные тела чаще всего движутся не равномерно. Например, все вы знаете, что автомобиль в начале своего движения из состояния покоя постепенно увеличивает свою скорость. Где-то в середине пути он, возможно, будет недолго двигаться с постоянной скоростью. А при торможении его скорость будет постепенно уменьшаться. То есть движение автомобиля является неравномерным. Поэтому описать его с помощью уравнения движения мы не можем, так как скорость тела постоянно меняется.
Но нам на помощь приходить понятие мгновенной скорости, то есть скорости точки в данный момент времени (или в данной точке траектории).
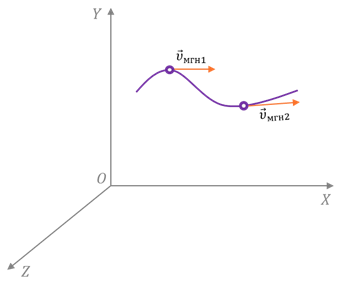
Чтобы понять, как определяется мгновенная скорость, рассмотрим неравномерное движение материальной точки по криволинейной траектории. Пусть в некоторый момент времени t она занимает положение М. А спустя некоторый промежуток времени Δt1 — положение М1.
Укажем на рисунке перемещение, которое совершила точка за этот промежуток времени.
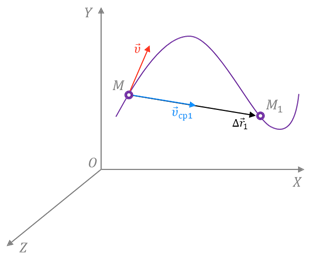
Если теперь мы с вами разделим это перемещение на промежуток времени, в течение которого оно произошло, то тем самым найдём такую скорость равномерного прямолинейного движения, с которой должна была бы двигаться точка, чтобы попасть из начального положения в конечное за определённый промежуток времени. Эта скорость называется средней скоростью перемещения. Она показывает, какое перемещение в среднем совершала точка за единицу времени.
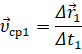
Направление этой скорости совпадает с направлением вектора перемещения точки.
Но как же нам определить скорость точки в положении М? Давайте попробуем уменьшить рассматриваемый промежуток времени. Из рисунка видим, что в этом случае точка совершит меньшее перемещение. Средняя же скорость точки на этом участке хотя и не равна скорости в точке М, но уже ближе к ней.
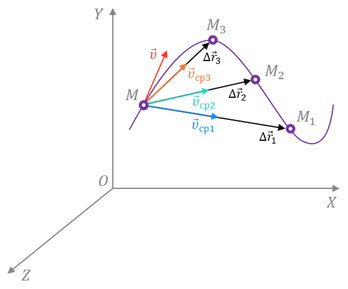
Если мы продолжим уменьшать промежутки времени и,
соответственно, перемещения, то очень скоро мы придём к тому, что средние
скорости будут незначительно отличаться друг от друга и от скорости точки в
положении М. В конце концов промежуток времени станет так мал, что можно
будет пренебречь изменением скорости за это время. Следовательно, при
стремлении промежутка времени к нулю отношение 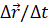 будет
стремиться к своему некоторому предельному значению.
будет
стремиться к своему некоторому предельному значению.
Физическая векторная величина, равная пределу отношения перемещения к промежутку времени, в течение которого это перемещение произошло, при стремлении промежутка времени к нулю, называется мгновенной скоростью:
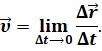
Направление вектора мгновенной скорости зависит от вида движения точки. Так, если точка движется прямолинейно, то направление мгновенной скорости совпадает с направлением движения. А вот в случае криволинейного движения вектор мгновенной скорости направлен по касательной к траектории.
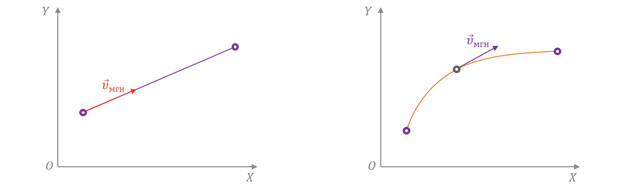
В этом легко убедиться, если понаблюдать за раскалёнными частицами, отрывающимися от точильного камня. Или за частицами грязи, вылетающими из-под колеса буксующего автомобиля.

Для описания неравномерного движения точки, помимо понятия средней скорости перемещения, в физике чаще используют понятие средней путевой скорости. Она определяется отношением пути к промежутку времени, за который этот путь пройдён:
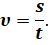
Проще говоря, средняя путевая скорость показывает, какой путь в среднем проходило тело за единицу времени.
Однако не стоит забывать о том, что средняя путевая скорость характеризует движение за весь промежуток времени в целом. Например, когда мы слышим, что расстояние между двумя городами автомобиль преодолел за 5 ч со скоростью 100 км/ч, мы понимаем, что в среднем он за каждый час проезжал сто километров. Но во время движения он мог заехать на заправку, где-то двигаться с бо́льшей или меньшей скоростью. Иными словами, средняя путевая скорость не даёт информации о скорости движения точки в каждый момент времени.
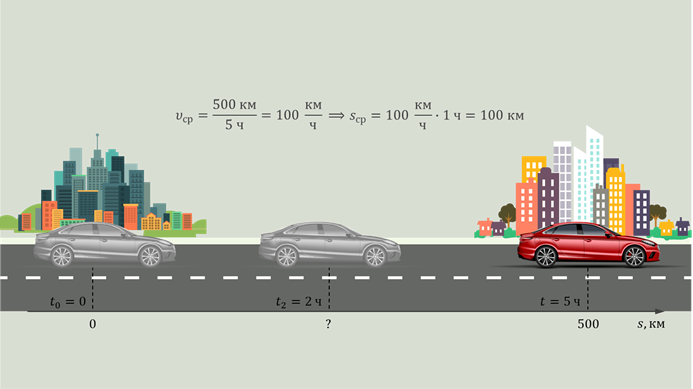
Для примера давайте с вами определим среднюю путевую скорость движения точки, если первую половину пути она преодолела со скоростью 15 м/с, а вторую — со скоростью 25 м/с.

Мы уже с вами не раз говорили о том, что характер движения точки зависит от того, относительно каких тел мы рассматриваем это движение (то есть от выбора системы отсчёта). Но так как тело отсчёта мы можем выбирать совершенно произвольно, то положение одного и того же тела можно одновременно рассматривать в разных системах координат.
Рассмотрим такой опыт. Пусть у нас есть стеклянная трубка, заполненная вязкой жидкостью. Опустим в неё тяжёлый шарик и будем перемещать трубку относительно школьной доски в горизонтальном направлении, не меняя ориентации трубки. Одновременно будем наблюдать за движением шарика и отмечать его положения через равные интервалы времени.
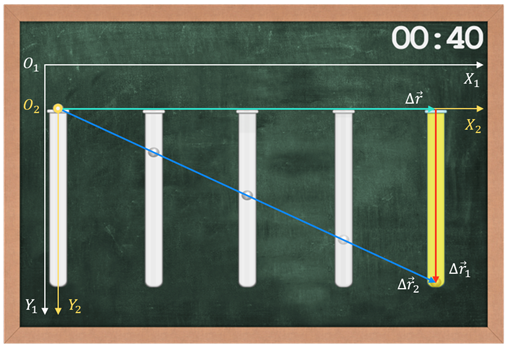
Теперь выберем две системы координат: одну свяжем с доской и назовём неподвижной, а вторую — с трубкой и назовём движущейся.
Из рисунка видно, что перемещение точки относительно неподвижной системы отсчёта равно векторной сумме её перемещения относительно движущейся системы и перемещения движущейся системы отсчёта относительно неподвижной:
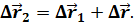
В этом состоит принцип независимости движений.
Теперь разделим записанное нами уравнение на промежуток времени, в течение которого произошли эти перемещения:
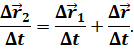
И учтём, что отношения перемещений к промежутку времени равны скоростям:
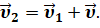
Таким образом получаем, что скорость тела относительно неподвижной системы отсчёта равна векторной сумме его скорости относительно подвижной системы отсчёта и скорости подвижной системы отсчёта относительно неподвижной.
Данное утверждение называется законом сложения скоросте́й Галилея. Он справедлив как для равномерного, так и для неравномерного движения. Только в этом случае складываются мгновенные скорости.
Однако этот закон нельзя применять для точек, движение которых происходит со скоростями, близкими к скорости света в вакууме.
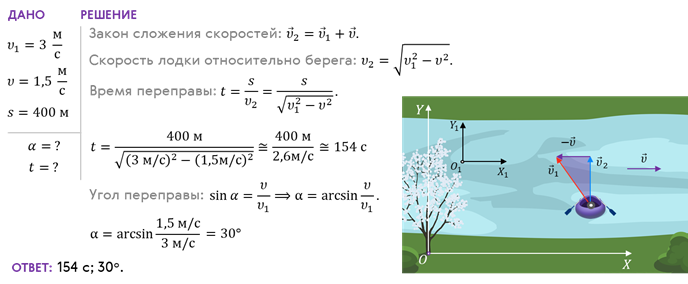
Для примера решим такую задачу. На какой угол следует отклонится от перпендикуляра к течению реки и сколько времени нужно плыть на лодке, чтобы пересечь реку перпендикулярно её течению, если скорость лодки относительно воды 3 м/с, скорость течения реки — 1,5 м/с, а ширина русла — 400 м?

 Получите свидетельство
Получите свидетельство Вход
Вход




 13400
13400

