Скорость и перемещение точки при РПД

В зависимости от вида траектории движения точки принято выделять прямолинейное и криволинейное движения. Очевидно, что самым простым и самым лёгким для описания является прямолинейное движение точки, особенно, когда это движение происходит с постоянной скоростью.

Давайте вспомним, что движение с постоянной скоростью называется равномерным. При таком движении точка за равные промежутки времени совершает одинаковые перемещения.

Скорость является важной величиной, характеризующей движение. Вам уже известно, что скорость является векторной величиной. Поэтому она считается заданной лишь тогда, когда известны её модуль и направление.

Теперь вспомним, что называется скоростью равномерного прямолинейного движения. Итак, пусть материальная точка, двигаясь прямолинейно и равномерно, переходит из положения 1 в положение 2 за некоторый промежуток времени Δt. При этом, что очевидно, точка совершит перемещение .

Разделив это перемещение на промежуток времени, в течение которого оно произошло, мы получим вектор скорости равномерного прямолинейного движения точки:

Напомним, что скорость обозначается греческой буквой «Ипсилон», но читаем мы её как «Вэ» (от латинского «велочитас» (vēlōcitās) — 'быстрый').

А единицей скорости в СИ является метр в секунду (м/с).

Так как промежуток времени — это скалярная величина, то из формулы следует, что направление вектора скорости при равномерном прямолинейном движении совпадает с направлением вектора перемещения. А её модуль не меняется с течением времени.

Теперь давайте с вами выясним, что такое модуль скорости:

Вам уже известно, что при равномерном прямолинейном движении модуль перемещения точки — это расстояние, которое она прошла за промежуток времени Δt. Поэтому модуль отношения, а значит, и модуль скорости — это величина, численно равная пути, пройденному точкой за единицу времени:

Но вернёмся к нашему рисунку и дополним его некоторыми построениями.

Итак, пусть положение точки в начальный момент времени t₀ задаётся радиус-вектором , а в момент времени t — .

Тогда можно записать, что промежуток времени Δt равен Δt = t – t₀. А перемещение точки — .

Выразим из него радиус-вектор, задающий конечное положение точки:

Полученное нами уравнение называется уравнением равномерного прямолинейного движения точки, записанном в векторном виде. Оно позволяет найти радиус-вектор точки при таком движении в любой момент времени, если известны скорость точки и радиус-вектор, задающий её положение в начальный момент времени.

На прошлых уроках мы с вами говорили о том, что основной задачей механики является определение координаты точки в любой момент времени. Давайте получим формулу для вычисления координаты точки при её равномерном прямолинейном движении для случая, когда направления радиус-вектора, задающего начальное положение точки, и вектора скорости совпадают.

Для описания движения выберем оси координат так, чтобы точка двигалась вдоль какой-либо её оси, например ОХ. А саму систему координат свяжем с одиноко стоящим деревом около путей. Учитывая, что проекции радиус-вектора на координатные оси равны координатам его конца, получаем:

r_x = x и r_0x = x₀.

Проекции же скорости и радиус-вектора на оси OY и OZ при таком выборе системы координат равны нулю.

Тогда уравнение равномерного прямолинейного движения точки примет тот вид, который вы сейчас видите на экране:

x = x₀ + υ_xt.

Записанное уравнение называется кинематическим законом равномерного движения или уравнением движения.

Из него следует, что для определения координаты движущегося тела в любой момент времени необходимо знать его начальную координату и проекцию скорости движения на ось.

В случае, когда направления радиус-вектора, задающего начальное положение точки, и вектора скорости не совпадают, то уравнение движения запишется в таком виде:

x = x₀ + υ_xt;

y = y₀;

z = z₀.

Необходимо помнить, что в формуле υ_x — это проекция вектора скорости. А она, как всякая проекция вектора, может быть больше или меньше нуля. Координата начального положения точки тоже может быть больше или меньше нуля, так как в момент начала наблюдения тело может находиться и по одну, и по другую сторону от начала отсчёта.

Для большей наглядности движение точки можно описывать с помощью графиков зависимости кинематических величин от времени. Рассмотрим их на таком примере. Итак, пусть из пунктов А и В, расстояние между которыми составляет 20 м, навстречу друг другу движутся две точки со скоростями, модули которых равны 2 м/с и 3 м/с соответственно. Постройте графики зависимости проекций скоростей точек от времени.

Полученные нами графики позволяют определить изменения координат точек (то есть их перемещение) за любой промежуток времени. Дело в том, что изменение координаты точки за некоторый промежуток времени численно равно площади прямоугольника, заключённого между графиком скорости, осью времени и перпендикулярами к этой оси́, восставленными из точек, соответствующих моментам начала и конца наблюдения.

Теперь построим графики зависимости координат точек от времени (их ещё называют графиками движения).

Из уравнений видно, что координаты точек при их равномерном прямолинейном движении линейно зависят от времени. Построим графики зависимости координат от времени, помня о том, что для построения прямой достаточно найти координаты двух любых её точек

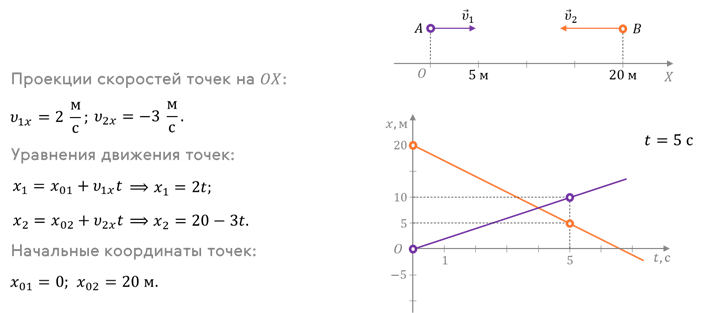
Для прямолинейного движения графики движения дают полное решение механической задачи, так как они позволяют определить координату тела в любой момент времени, в том числе и в моменты времени, предшествовавшие начальному (правда, если точка двигалась с той же скоростью и до начала наблюдения).

По виду этих графиков можно судить и о скорости тел: чем круче график (то есть чем больше его угол наклона к оси времени), тем больше скорость движения. При этом тангенс угла наклона графика к оси времени численно равен проекции скорости точки:

А координаты точки пересечения графиков соответствуют моменту встречи.

Для закрепления материала решим с вами парочку задач. Начнём с простой: На рисунке представлен график зависимости координаты туриста от времени. Опишите его движение.

И ещё одна небольшая задача. Две лодки плывут навстречу друг другу равномерно и прямолинейно. Скорость первой лодки 8 м/с, второй — 5 м/с. Определите время и координату их места встречи, если в начальный момент времени расстояние между лодками равно 130 м.

Эту же задачу можно было решить графически.