Мы с вами изучили равномерное прямолинейное движение, то есть движение, при котором точка за любые равные промежутки времени совершает одинаковые перемещения. Но, как мы уже отмечали, при реальном движении тел их скорости обычно меняются или по модулю, или по направлению, или же одновременно и по модулю, и по направлению. Например, когда автомобиль трогается с места, его скорость постепенно возрастает. А при торможении на перекрёстке, наоборот, — уменьшается.
При вращательном движении скорость любой точки дисков электрофорной машины изменяется лишь по направлению (конечно же, при условии, что число оборотов в единицу времени не изменяется).
Наконец, при выстреле из пушки под некоторым углом к горизонту скорость ядра будет изменяться как по модулю, так и по направлению.

При этом очевидно, что в рассмотренных нами примерах изменение скорости может происходит как очень быстро, так и достаточно медленно.
Физическая векторная величина, характеризующая быстроту изменения скорости, называется ускорением.
Давайте вспомним, как определяется ускорение точки. Для этого рассмотрим её неравномерное движение вдоль некоторой криволинейной траектории. Пусть в некоторый момент времени t она занимает положение М и имеет скорость υ. А спустя некоторый промежуток времени Δt1 — положение М1 и скорость υ1.

Найдём изменение скорости точки за это время как геометрическую разность векторов конечной и начальной скоростей и укажем эту разность на рисунке:

Если теперь мы с вами разделим вектор изменения скорости на промежуток времени, в течение которого это изменение произошло, то тем самым получим так называемый вектор среднего ускорения точки:

Он направлен точно так же, как и вектор изменения скорости.
Но как же нам определить ускорение точки в положении М?
Для этого будем уменьшать рассматриваемые промежутки времени и находить вектор
изменения скорости для каждого случая. Из полученного рисунка видим, что вектор
изменения скорости, а следовательно, и вектор среднего ускорения, уменьшается
по модулю и при этом меняется его направление. В конце концов промежуток времени
станет так мал, что можно будет пренебречь изменением скорости точки за это
время. Следовательно, при стремлении промежутка времени к нулю отношение  будет
стремиться к своему некоторому предельному значению.
будет
стремиться к своему некоторому предельному значению.
Физическая векторная величина, равная пределу отношения изменения скорости к промежутку времени, в течение которого это перемещение произошло, при стремлении промежутка времени к нулю, называется мгновенным ускорением (или просто ускорением):

Важно запомнить, что вектор ускорения направлен так же, как и вектор изменения скорости при стремлении промежутка времени к нулю. И в общем случае вектор ускорения не совпадает с направлением вектора скорости, а составляет с ним некоторый угол.
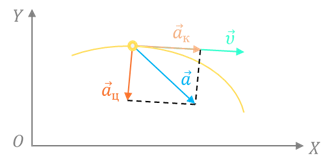
Как мы уже видели, при неравномерном движении по криволинейной траектории скорость точки непрерывно меняется по модулю и направлению. Поэтому вектор ускорения часто называют полным ускорением и представляют в виде суммы двух ускорений:

Первое ускорение называется тангенциальным (или касательным), так как направлено оно по касательной к траектории движения. Его модуль характеризует изменение модуля скорости:

Второе ускорение всегда направлено перпендикулярно вектору мгновенной скорости и поэтому называется нормальным (нормаль — это перпендикуляр) или центростремительным. Его модуль характеризует изменение скорости по направлению:

А вектор центростремительного ускорения в любой момент времени направлен к центру кривизны траектории.
Конечно же движение точки может происходить как с постоянным, так и с переменным ускорением. Так, если отношение изменения скорости к промежутку времени в течение которого это изменение произошло одинаково для любого интервала времени, то говорят, что точка движется с постоянным ускорением. А движение точки называют равноускоренным движением:

Из формулы видно, что если скорость и промежуток времени выражены в единицах СИ, то единицей измерения ускорения является метр на секунду в квадрате (м/с2).
Также из формулы следует, что за единицу ускорения в СИ принимается ускорение такого равноускоренного движения, при котором за 1 с скорость точки изменяется на 1 м/с.
Теперь давайте выясним, как зависит скорость точки от времени
при её равноускоренном движении. Итак, пусть в начальный момент времени t0 скорость точки равнялась  ,
а в момент времени t —
,
а в момент времени t — 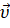 .
.

Тогда ускорение точки равно изменению вектора скорости к промежутку времени, за который это изменение произошло:

Если начальный момент времени принять равным нулю, то из этого уравнения легко получить формулу для определения скорости точки в любой момент времени при её равноускоренном движении — уравнение скорости:

Таким образом, чтобы определить скорость точки в произвольный момент времени, необходимо знать её начальную скорость и ускорение.
На практике при вычислениях скорости мы будем пользоваться формулами, в которые входят не векторы, а их проекции на соответствующие координатные оси:



Из записанных формул видно, что при равноускоренном движении скорость точки линейно зависит от времени. Значит, график скорости представляет собой прямую линию, наклонённую к оси времени под некоторым углом. При этом чем больше ускорение точки, тем больший угол с осью времени составляет график проекции скорости.
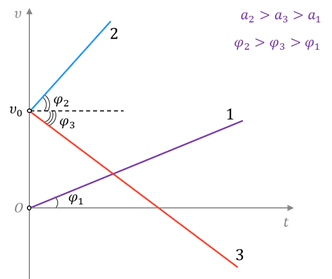
Теперь посмотрим на прямую 3. Что можно сказать о движении тела в этом случае?
Во-первых, очевидно, что за промежуток времени от нуля до t1 проекция скорости была положительна.
Во-вторых, скорость точки уменьшалась и в момент времени, равный t1 она стала равной нулю. Точка пересечения графика скорости с осью времени называется точкой поворота. В ней направление скорости меняется на противоположное, после чего тело начинает двигаться равноускоренно.
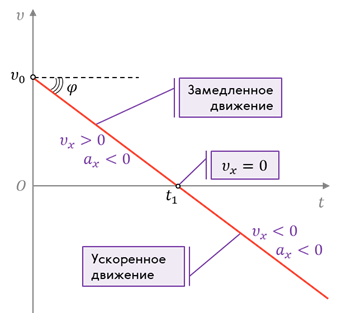
Теперь давайте вспомним, что основной задачей механики является определение положения точки в любой момент времени. Получим уравнения, которые позволяют это сделать для равноускоренного движения. Для примера рассмотрим случай, когда проекция начальной скорости и ускорения положительны. По аналогии со случаем равномерного прямолинейного движения логично предположить, что проекция перемещения, совершённого телом за время t, будет равна площади фигуры, ограниченной графиком, осью времени и перпендикуляром, восставленным к графику из точки t. В данном случае эта фигура — трапеция.

Для доказательства этого предположения рассмотрим очень малый промежуток времени Δt внутри выбранного интервала времени. По аналогии с мгновенной скоростью, если выбранный промежуток времени достаточно мал, то изменением скорости за это время можно пренебречь. То есть движение точки можно считать равномерным. Значит, проекция перемещения за это время будет равна площади этого маленького прямоугольника. При этом очевидно, что на такие узкие полоски мы можем разбить всю площадь фигуры под графиком скорости
Тогда, согласно рисунку, проекция перемещения при равноускоренном движении определяется площадью трапеции. Площадь же трапеции, как известно из геометрии, равна произведению полусуммы её оснований на высоту. В нашем случае длина одного из оснований численно равна проекции начальной скорости точки, второго — проекции скорости через время t. Высота же трапеции численно равна времени.

Теперь вспомним, что по определению проекция перемещения численно равна разности конечной и начальной координат точки:

Тогда после небольших математических преобразований получим формулу для определения координаты точки при её равноускоренном движении:

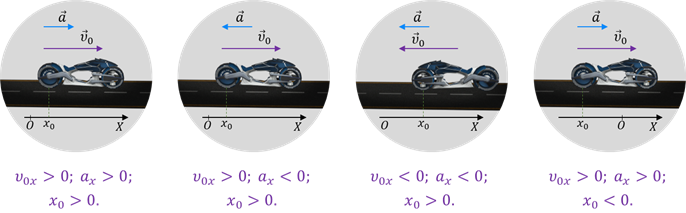
Важно помнить, что в формулу входят проекции начальной скорости и ускорения точки. А они могут быть как положительными, так и отрицательными. Координата начального положения точки также может быть больше или меньше нуля,
Если движение точки происходит в пространстве, то для определения оставшихся двух координат используют уравнения, имеющие аналогичной вид:


Записанные нами формулы называются кинематическими уравнениями движения точки в координатной форме. Они применимы для описания как прямолинейного, так и криволинейного движения.
В общем виде кинематические уравнения движения можно записать с помощью одного векторного уравнения:

Теперь для закрепления материала решим с вами одну небольшую задачку. Итак, на рисунке представлен график зависимости скорости точки от времени. Определите, в какой момент времени координата точки станет равной 30 м, если в момент начала наблюдения её координата равнялась –6 м. Определите скорость точки в этот момент времени.


 Получите свидетельство
Получите свидетельство Вход
Вход





 6760
6760

