Ускорение. Равноускоренное прямолинейное движение

Неравномерное движение — это такое движение, при котором тело, за любые равные промежутки времени совершает разные перемещения, или, говорят, меняется проекция вектора скорости.

Для описания быстроты изменения положения тела с течением времени при неравномерном движении, вводится понятие средней скорости. Она показывает, какое перемещение в среднем совершало тело за единицу времени:

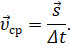
Но пользоваться этой формулой для определения модуля средней скорости можно лишь в том случае, если тело движется вдоль прямой в одну сторону. Во всех остальных случаях эта формула не работает.

Поэтому на практике пользуются понятием средней путевой скорости, с которым вы знакомы ещё с седьмого класса. Напомним, что средняя путевая скорость определяется отношением пути к промежутку времени, за который этот путь пройден. Она показывает, какой путь в среднем проходило тело за единицу времени:

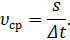
Однако следует помнить, что средняя скорость характеризует движение за весь промежуток времени в целом. Она не даёт информации о скорости движения в каждой точке траектории (или в каждый момент времени). Например, если мотоциклист преодолел путь в 300 километров за 6 часов, то средняя скорость его движения равна пятидесяти километрам в час. Иными словами, в среднем мотоциклист за каждый час проезжал 50 километров. Однако при этом он мог какое-то время стоять, какое-то время двигаться с большей или меньшей скоростью. Значит, зная среднюю скорость мотоциклиста за 6 часов, мы не сможем определить его положение через час или два.

Поэтому для описания такого движения вводится понятие мгновенной скорости, то есть скорости движения в данный момент времени или в данной точке траектории.

Теперь вспомним, как определить мгновенную скорость тела. Для этого предположим, что у нас есть шарик, который скатывается по наклонному жёлобу. Нас интересует мгновенная скорость шарика, например, в точке А его траектории. Выделим небольшой участок траектории, включающий в себя точку А. Разделив перемещение шарика на этом участке траектории, на соответствующий промежуток времени найдём среднюю скорость перемещения на этом участке. Это именно средняя скорость, потому что скорость непрерывно изменяется, и в разных местах участка она разная.

Рассмотрим меньшее перемещение — участок 2. Очевидно, что оно произойдёт за меньший промежуток времени. А средняя скорость шарика на этом участке хотя и не равна скорости в точке А, но уже ближе к ней.

При дальнейшем уменьшении перемещений и промежутков времени мы будем получать средние скорости, которые все меньше и меньше отличаются друг от друга и от мгновенной скорости шарика в точке А. В конце концов промежуток времени станет так мал, что можно будет пренебречь изменением скорости за это время (движение станет как бы равномерным). Тогда средняя скорость на этом участке и будет являться мгновенной скоростью шарика в точке А.

Таким образом, мгновенная скорость — это векторная физическая величина, равная отношению достаточно малого перемещения к малому промежутку времени, в течение которого это перемещение совершается:

Как следует из формулы, направление мгновенной скорости совпадает с направлением движения тела.

В дальнейшем мгновенную скорость мы будем называть просто скоростью.

Из всех видов неравномерного движения в школе изучают самое простое — прямолинейное равноускоренное движение. Так называют движение, при котором за любые равные промежутки времени скорость тела изменяется на одну и туже величину, а траекторией движения тела является прямая линия.

Для того, чтобы описать насколько быстро меняется скорость тела, в физике ввели величину, которую назвали ускорением тела.

Ускорение — это физическая величина, равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло:

Разумеется, ускорение, как и скорость, является векторной величиной. При этом направление вектора ускорения совпадает с направлением вектора изменения скорости тела.

Единицей измерения ускорения в системе СИ является

На прошлых уроках мы с вами, что основная задача кинематики сводится к нахождению положения тела в любой момент времени. Для того, чтобы её решить, нужно уметь находить скорость тела в любой момент времени. А для этого нам следует знать закон, по которому происходит изменение мгновенной скорости от времени для равноускоренного движения. Здесь всё просто. Нам нужно просто выразить вектор скорости из формулы определения ускорения тела:

Это есть уравнение скорости для равноускоренного движения.

Напомним, что по формулам, записанным в векторном виде, вычисления вести нельзя, поэтому перепишем уравнение в проекции на ось Ох:

Таким образом, зная проекцию вектора начальной скорости и проекцию вектора ускорения, можно вычислить проекцию вектора мгновенной скорости, которую будет иметь тело к концу любого заданного промежутка времени.

Как и в случае равномерного прямолинейного движения тела, зависимости кинематических величин от времени при равноускоренном движении можно изобразить графически.

Итак, на графике представлены графики зависимости ускорений для трёх тел от времени.

Как видим, эти графики являются прямыми линиями, параллельными оси времени. И это не удивительно, ведь при равноускоренном движении модуль и направление вектора ускорения не меняется. При этом обратите внимание на то, что график располагается над осью времени, если тело движется равноускорено. Под осью времени в случае равнозамедленного движения (то есть когда проекция ускорения на координатную ось меньше нуля). И будет совпадать с осью времени, если тело движется прямолинейно и равномерно.

Теперь изобразим графики зависимости скорости от времени.

Как мы знаем при равноускоренном движении скорость с течением времени изменяется со временем. При этом, как видно из уравнения, зависимость скорости от времени является линейной функцией и поэтому график скорости имеет вид прямой, наклоненной к оси времени. Причём, чем больше угол наклона, тем большее ускорение имеет тело.

А теперь подумайте, какие изменения движения тела в ней происходят?

Всё верно, в этой особой точке скорость тела меняет своё направление на противоположное. Такая точка называется точкой поворота.

Теперь настало время вспомнить, как определить местоположение тела при равноускоренном движении. Для этого воспользуемся графиком зависимости скорости тела от времени. Давай разобьём график скорости на такие бесконечно малые прямоугольные участки, чтобы на них скорость тела можно было считать постоянной.

Тогда перемещение за бесконечно малый промежуток времени будет равно площади закрашенной полоски. А найдя суммарную площадь всех малых фигур на выбранном интервале времени, а она будет равна площади трапеции, мы определим перемещение тела.

Теперь подставим в записанную формулу уравнение скорости при равноускоренном движении.

Раскрыв скобки и приведя подобные, получим уравнение перемещения при равноускоренном движении в проекциях на координатную ось:

Так как мы с вами рассматриваем прямолинейное движение, то в случае, когда скорость и ускорение направлены в одну сторону, модуль перемещения равен пройденному пути, поэтому, когда мы определяем модуль перемещения — мы определяем и пройденный путь.

Заменив проекции соответствующими векторами, получим уравнение перемещения в векторном виде:

Учитывая, что Δs_𝑥 = 𝑥 − 𝑥₀, преобразуем уравнение перемещения в проекциях на координатную ось:

Полученное равенство называется основным кинематическим уравнением равноускоренного движения.

Теперь давайте рассмотрим некоторые важные зависимости между величинами равноускоренного прямолинейного движения.

И так, для равноускоренного движения без начальной скорости путь, пройденный телом, пропорционален квадрату времени. Следовательно, пути, пройденные телом за одну, две, три, четыре и так далее секунды будут относиться как квадраты последовательных натуральных чисел:

s₁ : s₂ : s₃ = 1² : 2² : 3²

И ещё одна важная зависимость: для любого равноускоренного движения, пути, пройденные телом за любые равные промежутки времени, будут относиться как последовательный ряд нечётных чисел:

s_1-ю : s_2-ю : s_3-ю = 1 : 3 : 5

Так как проекция перемещения квадратично зависит от времени, то графиком перемещения для равноускоренного движения является парабола, положение вершины которой зависит от направлений начальной скорости и ускорения тела.

Здесь стоит обратить внимание на то, что для равноускоренного движения графиком движения (то есть графиком зависимости координаты тела от времени), тоже является парабола, положение вершины которой, как и в случае с перемещением, так же зависит от направлений начальной скорости и ускорения тела.