Признаки делимости на 10, на 5 и на 2

Представим себе такую историю…

– Саша, чем ты занимаешься? – спросил у друга Паша.

– Родители купили новый альбом для моих марок, – ответил Саша. — Вот, хочу разложить марки по листам. Да не знаю, как мне это сделать, чтобы на каждом листе получилось поровну.

– А сколько всего у тебя марок? – спросил Паша.

– 90, – ответил Саша, – но чем это может помочь?

– Да, всё просто – сказал Паша. Число 90 делится на 2, на 5 и на 10. Значит, ты можешь расположить на каждом листе альбома либо по 2, либо по 5, либо по 10 марок. Тогда на каждом листе их будет одинаковое количество.

– Паша, а как ты узнал, что число 90 делится на 2, на 5 и на 10? – спросил Саша. Ты же вроде на листке ничего не делил, да и калькулятором не пользовался.

– Чтобы быстро ответить на вопрос, делится ли одно число на другое без остатка, не всегда нужно выполнять деление – сказал Паша. Для некоторых делителей есть способ более удобный: для них существуют признаки делимости.

– Что это ещё за признаки такие? – спросил Саша.

– Вообще, признак делимости – это правило, которое позволяет сравнительно быстро определить, делится ли это число на заданное без остатка – сказал Паша.

– А чтобы нам с тобой в этом разобраться лучше, давай поговорим с Мудряшом. Он уж точно всё знает!

– Ребята, прежде чем я вам помогу разобраться с признаками деления, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

 – Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было получиться!

– Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. Деление чисел издавна считалось задачей, куда более трудной, чем умножение. Поэтому делить люди научились гораздо позже, чем умножать. Многие математики долго занимались поиском наиболее простого способа деления чисел. Один из них вы уже знаете – это деление уголком. Однако на деление уголком зачастую тратится много времени. А ведь бывают такие ситуации, когда необходимо быстро определить, делится ли одно число на другое или нет. Вот именно в таких ситуациях на помощь приходят признаки делимости. Сегодня я вам расскажу о признаках делимости на 10, на 5 и на 2. И начнём мы с признака делимости на 10.

– Давайте выпишем ряд чисел кратных 10 – предложил ребятам Мудряш.

– Числа кратные 10 будут следующими – начали мальчишки, – само число 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120 и так далее.

– Молодцы! – похвалил ребят Мудряш. Что общего можно заметить у всех этих чисел?

– Все числа этого ряда заканчиваются цифрой 0 – ответили мальчишки.

– Правильно! – согласился Мудряш. Последняя цифра каждого из этих чисел равна 0. Так как мы с вами выписывали ряд чисел кратных 10, то с уверенностью можем сказать, что все эти числа делятся нацело на 10. Посмотрите, каждое из них можно представить в виде произведения двух натуральных чисел, одно из которых равно 10. Например, , ,  и так далее.

– А теперь давайте рассмотрим число сто тридцать семь – предложил Мудряш. Как вы думаете, будет ли оно делиться на 10?

– Последняя цифра этого числа не равна 0 – сказал Саша. Значит, число 137 не делится нацело на 10.

– Действительно – согласился Мудряш. Давайте перепишем это число в немного другом виде. Число 137 можно записать так: . Мы с вами представили число 137 в виде суммы двух слагаемых. Обратите внимание, одно слагаемое, число 130, делится нацело на 10, а вот другое число 7, – не делится нацело на 10. Мы с вами уже знаем, что если число а делится нацело на число k, а число b не делится нацело на число k, то сумма а + b не делится нацело на число k. Значит, наша сумма не делится нацело на 10. Следовательно, и число 137 не делится нацело на 10.

– Запомните! – сказал Мудряш. – Если запись натурального числа оканчивается цифрой 0, то это число делится нацело на 10.

Если запись натурального числа оканчивается любой цифрой, отличной от 0, то число не делится нацело на 10.

Эти два утверждения называют признаком делимости на десять.

– А теперь давайте выпишем ряд чисел кратных 5 – предложил ребятам Мудряш.

– Числа кратные 5 будут такими – начали мальчишки, – само число 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105 и так далее.

– Молодцы! – похвалил ребят Мудряш. А что общего можно заметить в этих числах?

– Все числа этого ряда заканчиваются цифрой 5 или 0 – сказали мальчишки.

– Верно! – согласился Мудряш. Из нашего ряда чисел кратных 5 видно, что все эти числа оканчиваются цифрой 5 или 0.

Запомните! Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится нацело на 5.

Если запись натурального числа оканчивается любой цифрой, отличной от 0 или 5, то это число не делится нацело на 5.

Эти два утверждения называют признаком делимости на 5.

– С помощью признака делимости на 5 можно узнать, не выполняя деления, делятся ли на 5, например, числа  и .

– Число 366 625 делится нацело на 5, так как оно оканчивается цифрой 5 – начали мальчишки. – Вот число 8 623 451 не делится нацело на 5, так как оно оканчивается цифрой 1.

– Молодцы! – похвалил ребят Мудряш. Скажите, а как узнать, чётно число или нечётно?

– Чтобы узнать чётно число или нечётно, нужно проверить делится ли оно на 2 – ответили мальчишки.

– Правильно! – согласился Мудряш. Но при этом ответ можно дать, не выполняя деления. Стоит только взглянуть на последнюю цифру числа. Чтобы разобраться в том, как получать ответ, давайте запишем ряд чётных чисел.

– Чётные числа – начали мальчишки – это 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26 и так далее.

– Верно! – сказал Мудряш. Обратите внимание на последние цифры этих чисел. Давайте составим из них новый ряд.

– Это будут цифры – начали ребята, – 2, 4, 6, 8, 0, 2, 4, 6, 8, 0, 2, 4, 6 и так далее.

– Молодцы! – похвалил ребят Мудряш. А теперь давайте запишем ряд нечётных чисел.

– Нечётные числа – начали ребята, – это 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25 и так далее.

– Всё верно! – согласился Мудряш. А теперь составьте ряд из цифр, на которые оканчиваются нечётные числа.

– 1, 3, 5, 7, 9, 1, 3, 5, 7, 9, 1, 3, 5 и так далее – назвали мальчишки.

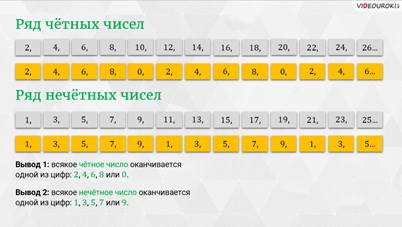
– Какой вывод можно сделать – спросил Мудряш.

– Всякое чётное число оканчивается одной из цифр 2, 4, 6, 8 или 0 – начали мальчишки, – а всякое нечётное число оканчивается одной из цифр 1, 3, 5, 7 или 9.

– Молодцы! – похвалил ребят Мудряш. Теперь легко догадаться, как определить чётное число или нечётно.

Запомните! Если запись натурального числа оканчивается чётной цифрой, то это число делится нацело на 2.

Если запись натурального числа оканчивается нечётной цифрой, то это число не делится нацело на 2.

Эти два утверждения называют признаком делимости на 2.

– Интересно знать, что основоположниками теории делимости на 2 являются Пифагор и его ученики. Они разбили все числа на чётные – «женские» и нечётные – «мужские». И когда пифагорейцы, по обычаю античных времён, приносили подношения высшим силам, богам выделялось нечётное количество предметов, а богиням – чётное.

А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.

Задание первое: запишите числа, большие 455, но меньшие 466, если известно, что они: чётные; кратны 5; кратны 10.

Решение: сначала выпишем числа большие 455, но меньшие 466. Это будут числа: 456, 457, 458, 459, 460, 461, 462, 463, 464 и 465. Мы знаем, что всякое чётное число оканчивается одной из цифр 2, 4, 6, 8 или 0. Тогда чётными числами будут 456, 458, 460, 462 и 464.

Теперь нам нужно выписать числа кратные 5. Мы знаем, что если запись натурального числа оканчивается цифрой 0 или 5, то это число делится нацело на 5. Значит, кратными 5 будут 460 и 465.

И осталось выписать числа кратные 10. Мы знаем, что если запись натурального числа оканчивается цифрой 0, то это число делится нацело на 10. Из наших чисел только число 460 кратно 10.

Следующее задание: напишите наибольшее трёхзначное число, кратное 5, но не кратное 2.

Решение: наибольшие трёхзначные числа начинаются с 990, и заканчиваются 999, так как следующее число уже будет четырёхзначным. Мы знаем, что если запись натурального числа оканчивается цифрой 0 или 5, то это число делится нацело на 5, а если запись натурального числа оканчивается чётной цифрой, то это число делится нацело на 2. Исходя из этого, наше число должно оканчиваться цифрой 5. Число, оканчивающееся на 0, не подходит, так как 0 относится к чётным числам и тогда число будет делиться на 2. А это противоречит нашему условию. Значит, нам подходит только число, которое оканчивается цифрой 5. И это число 995. Оно будет наибольшим трёхзначным числом, кратным 5, но не кратным 2.