Представим себе такую историю…
– Саша, чем ты занимаешься? – спросил у друга Паша.
– Я хочу к вечеру подготовить сюрприз для родителей, – сказал Саша.
– Сюрприз – это здорово! – поддержал друга Паша. — И какой же сюрприз ты готовишь?
– Я планирую самостоятельно испечь кексы к ужину, – ответил Саша. — Вот, даже рецептик нашёл и уже купил формочки для кексов.
– Хороший сюрприз! – согласился Паша.
– Вот теперь только не могу определиться с их количеством, – задумался Саша. Сколько мне нужно приготовить кексов, чтобы на ужин их разделить поровну между мной, мамой и папой?
– Ну давай подумаем вместе, – предложил Паша. — 1 кекс или 2 кекса на троих поделить не получится. А вот 3 кекса ты спокойно сможешь разделить на троих.
– Ну да! – согласился Саша. — Но это что, получится по 1 кексу каждому? Что такое съесть по 1 кексу? В общем, 3 кекса это как-то маловато, не подходит.
– Хорошо! – продолжил Паша. — 4 кекса или 5 кексов снова нельзя разделить на троих. Значит, ты можешь приготовить 6 кексов. Тогда каждому достанется по 2.
– Знаешь, лучше я сделаю 9 кексов, – решил Саша. — Тогда получится по 3 кекса каждому. Красивое число, правда?

– Согласен! – ответил Паша.
– Да, и долго же нам с тобой пришлось перебирать числа, – задумался Саша. Интересно, а есть ли какой-нибудь способ побыстрее определиться?
– Я думаю, существуют разные способы, – сказал Паша. — А чтобы нам с тобой в этом разобраться лучше, давай поговорим с Мудряшом. Он уж точно всё знает!
– Ребята, прежде чем я вам помогу разобраться с вашим вопросом, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было получиться!
– Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. — Но прежде, ответьте на мой вопрос: что вы понимаете под действием – деление?
– Деление – это действие разложения величины на равные части, – ответили мальчишки.
– Молодцы! – похвалил ребят Мудряш. — Одно натуральное число можно разделить на другое натуральное число либо нацело, как, например, 3 на 3, 6 на 3, 9 на 3 и так далее, либо с остатком, как, например, при делении 4, 5, 7, 8 на 3.

Запомните! Если
одно натуральное число нацело делится на другое натуральное число, то первое
называют кратным второму, а второе – делителем первого. Обратите
внимание, здесь прозвучало одно важное слово – нацело, то есть деление без остатка.
Натуральное число а делится нацело на натуральное число b, если найдётся
натуральное число c
такое, что справедливо равенство 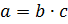 .
.
Если натуральное число а делится нацело на натуральное число b, то число а называют кратным числа b, а число b – делителем числа а.

– В случае с Сашиным сюрпризом, вы заметили, что 9 делится нацело на 3. Число 3 называют делителем числа 9, а число 9 – кратным числа 3.

– А сколько существует кратных числу 3? – решили уточнить мальчишки.
– Давайте вместе найдём кратные числу 3, – предложил Мудряш. — Для начала запишем натуральный ряд. А теперь под ним будем записывать произведения чисел этого ряда на 3. Получим: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33 и так далее. Мы с вами получили новый ряд – ряд кратных числа 3. Несложно понять, по какому правилу идут в нём числа.

– Этот ряд начинается с числа 3, а каждое последующее число больше предыдущего на 3, – сказали ребята.
– Правильно! – согласился Мудряш. — Кроме того, раз ряд натуральных чисел бесконечен, то и ряд кратных числа 3 тоже бесконечен. Получается, что чисел, кратных числу 3, бесконечно много. Поэтому всех их перечислить нельзя.
–
Вообще, если обозначить натуральное число буквой а, то ряд его кратных можно
записать так: 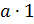 ,
, 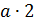 ,
, 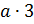 ,
, 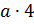 ,
, 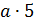 ,
, 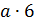 ,
, 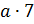 ,
, 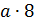 ,
, 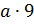 и так далее.
Такой ряд начинается с числа а, каждое последующее
число в нём больше предыдущего на а; кроме того, этот ряд бесконечен.
и так далее.
Такой ряд начинается с числа а, каждое последующее
число в нём больше предыдущего на а; кроме того, этот ряд бесконечен.

Запомните! Для
любого натурального числа а каждое из чисел 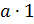 ,
, 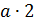 ,
,
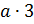 ,
,
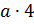 ,
,
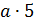 и
так далее является кратным числа а.
и
так далее является кратным числа а.
– Может, вы сможете назвать самое маленькое и самое большое кратные числа 3?
– Среди чисел, кратных 3, наибольшего нет, ведь мы уже сказали, что ряд кратных чисел бесконечен, – начали мальчишки, а вот наименьшее есть – это само число 3.
– Молодцы! – похвалил ребят Мудряш. — Запомните! Среди чисел, кратных натурального числа а, наибольшего нет, а наименьшее – это само число а.
– А теперь давайте поговорим о делителях числа, – продолжил Мудряш. — Запомните! Делителем b натурального числа а называют натуральное число b, на которое а делится без остатка.
– Может, вы сможете назвать делители числа 30, – спросил Мудряш.
– Так… – начали ребята, – делителями числа 30 будут числа: 1, 2, 3, 5, 6, 10, 15 и само число 30.
– Правильно! – согласился Мудряш. — А теперь назовите наименьший и наибольший делители числа 30.
– Наименьшим делителем числа 30 будет 1, – начали мальчишки, – а наибольшим – само число 30.

– Всё правильно! – подтвердил Мудряш. — Запомните! Наименьшим делителем любого натурального числа а является число 1, а наибольшим – само число а.
– Обратите внимание: число 30 не делится нацело, например, на число 9. Значит, число 9 не является делителем числа 30, в свою очередь, и число 30 не будет кратным числу 9.
– А теперь давайте рассмотрим следующие пары чисел: 21 и 36, 4 и 8, 9 и 7, 35 и 17. Каждое из чисел первой пары делится нацело на 3, кстати, и их сумма, число 57, также делится нацело на 3.
Запомните! Если каждое из чисел а и b делится нацело на число k, то и сумма а + b также делится нацело на число k.
– Перейдём к следующей паре. Каждое из чисел 4 и 8 не делится нацело на 3, а вот их сумма, число 12, делится нацело на 3.
Что касается пары чисел 9 и 7, то каждое из этих чисел не делится нацело на 5, и их сумма, число 16, также не делится нацело на 5.
Запомните! Если ни число а и ни число b не делятся нацело на число k, то их сумма а + b может делиться, а может и не делиться нацело на число k.
– И последняя пара чисел. Число 35 делится нацело на число 7, а вот число 17 на число 7 не делится нацело. Сумма этих чисел – число 52 также не делится нацело на число 7.
Запомните! Если число а делится нацело на число k, а число b не делится нацело на число k, то сумма а + b не делится нацело на число k.

– А как лучше и правильнее говорить: «Число а делится нацело на число b», «Число b является делителем числа а», «Число а кратно числу b», «Число а является кратным числа b»? – решили спросить мальчишки.
– Здесь все утверждения будут верными, – сказал Мудряш. — Поэтому, как говорить, вы можете выбирать на свой вкус. А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.
Задание первое: выберите из чисел 20, 1, 5, 3, 4, 8, 16, 24, 15, 12 те, которые являются: делителями 15; кратными 4.
Решение: сначала нам нужно выбрать числа, которые будут являться делителями 15. Число 15 без остатка делится на 1, 5, 3 и 15. Осталось выбрать числа кратные 4. На число 4 без остатка будут делиться числа 20, 4, 8, 16, 24 и 12.

Следующее задание: в вазе лежит 30 конфет. Сколько конфет нужно добавить, чтобы 7 мальчиков смогли разделить их поровну между собой?
Решение: чтобы ответить на вопрос задачи, нам нужно выписать кратные числа 7. Это будут: 7, 14, 21, 28, 35, 42, 49 и так далее. Мы знаем, что в вазе лежит 30 конфет. Значит, чтобы мальчики смогли разделить все конфеты поровну, в вазу можно добавить 5, 12, 19 и так далее конфет.

И последнее задание: в классе 28 учеников. На уроках физкультуры они обычно строятся в 2 шеренги. Можно ли построить их: в 3 одинаковые шеренги; в 4 одинаковые шеренги; в 5 одинаковых шеренг; в 7 одинаковых шеренг?
Решение: чтобы ответить на вопросы задачи, мы должны выписать все делители числа 28. Число 28 нацело делится на числа: 1, 2, 4, 7, 14 и 28. Зная это, можем сказать, что из 28 учеников нельзя построить 3 и 5 одинаковых шеренг. Зато их можно построить в 4 или 7 одинаковых шеренг.


 Получите свидетельство
Получите свидетельство Вход
Вход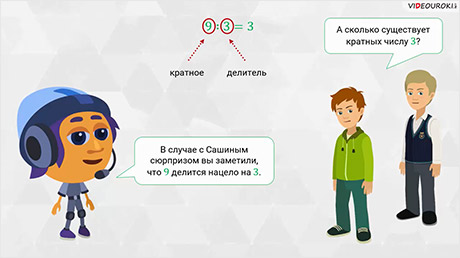



 0
0 3997
3997

