
Звёздчатые многогранники

Теория многогранника - это не только наследие прошлого. Спустя две тысячи лет многие люди по-прежнему очарованы ее эстетическими корнями. То, что многогранник и по сей день не утратил своей привлекательности, очень убедительно, как и его использование в науке, искусстве и архитектуре. Многогранники существуют в природе повсюду вокруг нас.
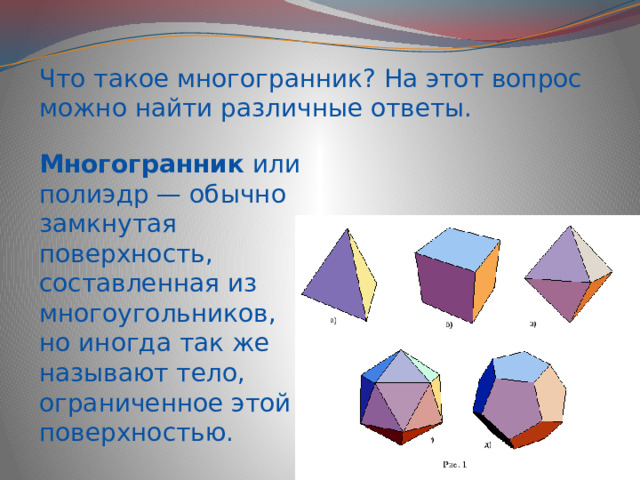
Что такое многогранник? На этот вопрос можно найти различные ответы.
Многогранник или полиэдр — обычно замкнутая поверхность, составленная из многоугольников, но иногда так же называют тело, ограниченное этой поверхностью.

Звёздчатый многогранник (звёздчатое те-ло) — невыпуклый многогранник , грани которого пересекаются между собой. Как и у незвёздчатых многогранников, грани попарно соединяются в рёбрах (при этом внутренние линии пересечения не считаются рёбрами).

Малый и большой звёздчатые додекаэдры, которые иногда именуют « многогранники Кеплера», впервые были полностью описаны в трактате Иоганна Кеплера 1619 года.
Иога́нн Ке́плер — немецкий математик, астроном, механик, оптик, первооткрыватель законов движения планет Солнечной системы.

Оставшуюся пару «отыскал» француз Луи Пуансо : большой звёздчатый додэкаэдр и большой икосаэдр
Луи́ Пуансо́ — французский математик и механик, академик Парижской Академии наук; пэр Франции, сенатор. Известен своими трудами в области геометрии и механики.

Тело Кеплера — Пуансо — тело, представляющее собой правильный звёздчатый многогранник, не являющийся соединением платоновых и звёздчатых тел.

Снежинки- это звёздчатые многогранники
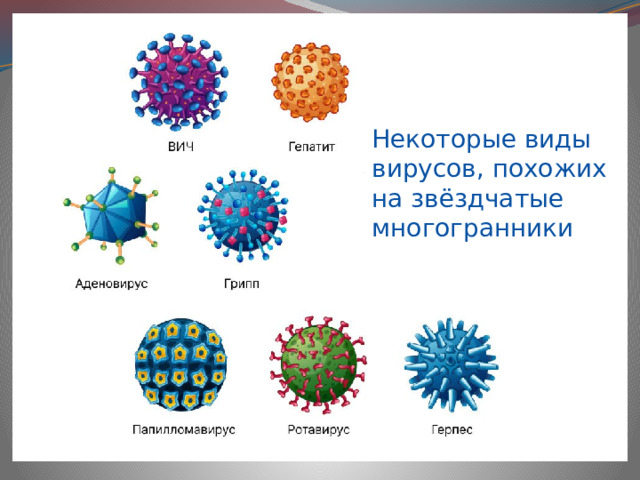
Некоторые виды вирусов, похожих на звёздчатые многогранники

Примеры в ювелирной промышленности

Примеры в архитектуре

Примеры в интерьере


Создание модели звёздчатого октаэдра
1 Разметка шаблона
На одном листе А4 чертим большую «выкройку»(в виде равностороннего треугольника) - макет будущего тетраэдра. Стороны = 20 см + 1 см добавляем по краям(для линий сгиба)
На другом, чертим четыре маленькие
«выкройки»- макеты
трех тетраэдров.
Стороны = 10 см+0,5 см
добавляем по краям
(для линии сгиба)

2 Склейка и готовая модель
Вырезаем получившиеся треугольники,
сгибаем вдоль линий сгиба и склеиваем
по краям.

На грани большого тетраэдра, наклеиваем четыре маленьких тетраэдра, таким образом, чтобы вершины маленьких совместились на середине ребра большого тетраэдра.

Заключение
Работая над проектом, я познакомилась с интереснейшим, красивейшим, загадочным миром многогранников и его подвидом звёздчатыми многогранниками: они связаны с такими науками, как биология, химия, встречаются в природе иархитектуре. Именно это я попыталась показать, изучая тему «Звёздчатые многогранники».

 Получите свидетельство
Получите свидетельство Вход
Вход












 Звёздчатые многогранники (5.22 MB)
Звёздчатые многогранники (5.22 MB)
 0
0 510
510 2
2 Нравится
0
Нравится
0


