Знаменитое число ПИ
Содержание работы
Введение «День рождения Пи».
Вычисления числа Пи в средние времена.
Практическое применение числа Пи.
Метод Монте-Карло, выводы.
Моделирование метода Монте-Карло на Turbo Pascal.
Метод «падающей иглы».
Метод вычисления Пи с помощью бесконечных рядов.
Современные расчеты числа Пи.
Выводы.
В прошлом году я на занятиях математического кружка заинтересовался числом, у которого есть день рождения. Решил попробовать вычислить число ПИ различными доступными методами, возможно, с применением программирования.
День числа Пи отмечается некоторыми математиками 14 марта в 1:59 (в американской системе записи дат — 3/14; первые разряды числа π = 3,14159). Обычно празднуют в 1:59 дня (в 12-часовой системе), но придерживающиеся 24-часовой системы света времени считают, что это 13:59, и предпочитают отмечать ночью. В это время читают хвалебные речи в честь числа пи, его роли в жизни человечества, рисуют антиутопические картины мира без пи, едят пи-рог (pie), пьют напитки и играют в игры, начинающиеся на «пи».
14 марта, в день числа пи, родился Альберт Эйнштейн.
В каждой книге по занимательной математике мы непременно найдем историю уточнения значения числа пи. Сначала, в древних Китае, Египте, Вавилоне и Греции для расчетов использовали дроби, например, 22/7 или 49/16.
| Формулы для вычисления π | Значения этих формул | Когда и где были выведены формулы |
| 4*(1-1/9)2 | = 3, 1604 | Египет, около 1650 г до нашей эры |
| 3 + 1/8 | = 3, 125 | Вавилон, около 500 г до нашей эры.
|
| 3 + 1/7 | = 3, 1428 | Архимед, около 220 г до нашей эры. |
| 355/113 | = 3, 1415 | Китай, около 500 г нашей эры. |
В Средние века и эпоху Возрождения европейские, индийские и арабские математики уточнили значение π до 40 знаков после десятичной точки, а к началу компьютерной эпохи усилиями многих энтузиастов количество знаков было доведено до 500.
Такая точность имеет чисто академический интерес, а для практических нужд в пределах Земли достаточно 10 знаков после запятой. При радиусе Земли 6400 км или 6,4·109 мм, получится, что, отбросив двенадцатую цифру π после запятой, мы при вычислении длины меридиана, ошибемся на несколько миллиметров. А при расчете длины земной орбиты вокруг Солнца (ее радиус 150 млн км = 1,5·1014 мм) для такой же точности достаточно использовать число пи с четырнадцатью знаками после запятой. Среднее расстояние от Солнца до Плутона — самой далекой планеты Солнечной системы — в 40 раз больше среднего расстояния от Земли до Солнца. Для вычисления длины орбиты Плутона с ошибкой в несколько миллиметров достаточно шестнадцати знаков пи. Да что уж там мелочиться, диаметр нашей Галактики около 100 тыс. световых лет (1 световой год примерно равен 1013 км) или 1019 мм, а ведь еще в XVII веке были получены 35 знаков π, избыточные даже для таких расстояний.
Число Пи одна из фундаментальных математических констант. Оно встречается во многих уравнениях различных направлений науки. Например, в уравнениях гравитационного поля Эйнштейна, в уравнениях, связанных с образованием радуги, в уравнениях описывающих распространение зыби при падении дождевой капли в воду, в уравнении нормального распределения Гаусса, в уравнении движения маятника, во многих геометрических задачах, в задачах связанных с волнами, в задачах навигации и т.д.
Иррациональность этого числа, заключающаяся в том, что его нельзя представить отношением p/q, где q≠0 и p, q - натуральные числа, была доказана Ламбертом в 1761 г. Трансцендентность числа π доказал Линдеман в 1882 г.
Мы знаем, что число выражает отношение длины окружности к своему диаметру. Первым ввел обозначение отношения длины окружности к диаметру современным символом английский математик Джонсон в 1706 г. В качестве символа он взял первую букву греческого слова “ПЕРИФЕРИЯ”, что в переводе означает “ОКРУЖНОСТЬ”. Введенное Джонсоном обозначение стало общеупотребительным после опубликования работ Эйлера, который воспользовался введенным символом впервые в 1736 году.
Начертим на плотном картоне окружность, радиусом R, вырежем круг и обмотаем вокруг него тонкую нить. Измерив длину одного полного оборота нити, разделим на длину диаметра окружности.
Получившееся частное будет приближенным значением числа . Этот способ вычисления числа я использовал в прошлом году. Это очень простой способ. Я решил продолжить исследование числа π, попытаться самостоятельно вывести его значение разными методами и способами. Это оказалось очень занимательно. Для решения некоторых задач мне пришлось начать изучение языка программирования Turbo Pascal.
В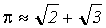 практических расчетах этого времени часто применялось приближенное значение:
практических расчетах этого времени часто применялось приближенное значение:
После доказательства трансцендентности числа "пи" стало ясно, что его нельзя выразить подобными формулами. Но я все равно решил проверить эту формулу с помощью линейного алгоритма на языке программирования Turbo Pascal.
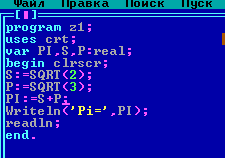
Результат удивил меня. Ответ был очень близок значению Пи в своих первых цифрах: 3, 146264.
Метод Монте-Карло
Тогда я решил продолжить свое исследование и прочитал про метод Монте-Карло. Свое экзотическое название получил от города Монте-Карло в княжестве Монако, знаменитого своими игорными домами. Дело в том, что метод требует применения случайных чисел, а одним из простейших приборов, генерирующих случайные числа, может служить рулетка. Можно получить случайные числа и при помощи дождя.
Для опыта приготовим кусок картона, нарисуем на нем квадрат и впишем в квадрат четверть круга. Если такой чертеж некоторое время подержать под дождем, то на его поверхности останутся следы капель. Подсчитаем число следов внутри квадрата и внутри четверти круга. Их отношение будет приближенно равно отношению площадей этих фигур, так как попадание капель в различные места чертежа равновероятно.
Это один из самых простых и понятных методов вычисления Пи. Суть этого метода сводится к простейшему перебору точек на площади. Расчета заключается в том, что мы берем квадрат со стороной a = 2 R, вписываем в него круг радиусом R. Рассмотрим произвольный квадрат с центром в начале координат и вписанный в него круг. Будем рассматривать только первую координатную четверть. В ней будет находиться четверть круга и четверть квадрата. Обозначим радиус круга R, тогда четверть квадрата тоже будет квадратом (очевидно) со стороной R.
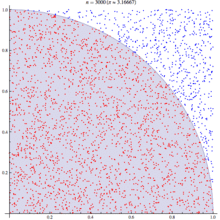
И начинаем наугад ставить точки внутри квадрата (Рис. 1). Некоторые из этих точек попадают в круг внутри квадрата, а некоторые нет. Геометрически, вероятность P того, что точка попадет в круг, равна отношению площадей круга и квадрата:
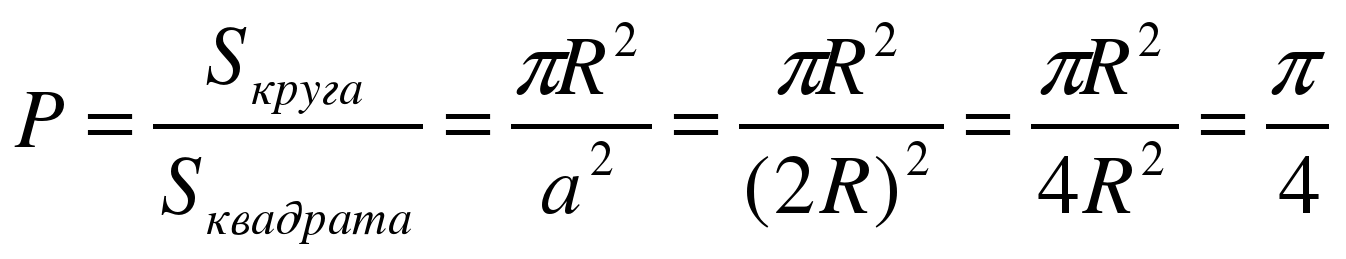
Выглядит это так:
 a=2R
a=2R
Эта же вероятность может быть найдена как вероятность попадания точки в круг: посчитать количество точек, попавших в круг, и поделить их на общее количество поставленных точек:
Р =Nкруга / Nквадрата, где
Nкруга –это количество точек, которые попали в круг; Nквадрата – это количество точек, которые попали в квадрат.
Результаты эксперимента. Эксперимент помогали проводить ученики нашей школы. Они вписывали круг в квадрат, забрызгивали каплями, считали точки, попавшие в квадрат, и отдельно точки, попавшие в круг. Я обрабатывал их результаты и с помощью формулы и калькулятора вычислял значение Пи. Значение числа Пи получилось в пределах от 2,2 до 3,2. Метод мне показался интересным, но, к сожалению, точного значения Пи мне не удалось получить. Проблема, которую я вижу, следующая:
Для точности результата необходимо брать очень много точек;
Большое количество точек очень сложно посчитать.
Поэтому я попытался запрограммировать ситуацию набрызгивания точек через Turbo Pascal с помощью случайно выставленных точек в круг радиуса R=1. Преимущество этого метода в том, что количество точек можно задать сколько угодно большое, и их количество определяется очень точно. Для этого была создана программа.
З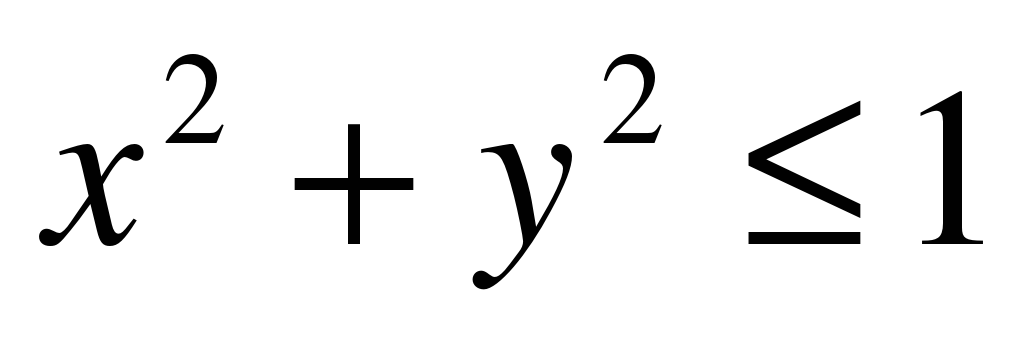 десь: random – функция, которая задает случайные координаты х и у для точки. Попадание точки в круг задается условием
десь: random – функция, которая задает случайные координаты х и у для точки. Попадание точки в круг задается условием
N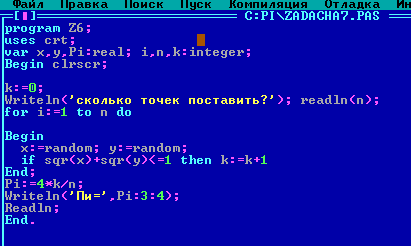 – количество «набрызганных» точек, K – количество точек, попавших в круг. Чем больше задать точек N, тем точнее получаются результаты.
– количество «набрызганных» точек, K – количество точек, попавших в круг. Чем больше задать точек N, тем точнее получаются результаты.
Результаты:
N= 1000, = 3, 1560
N= 2000, = 3, 1680
N= 3000, = 3, 1333
N= 4000, = 3, 1410
N= 5000, = 3, 1456
N= 10000, = 3,1420
Метод «падающей иголки»
Возьмем обыкновенную швейную иголку и лист бумаги. На листе проведем несколько параллельных прямых так, чтобы расстояние между ними были равны и превышали длину иголки. Введем обозначения а – расстояние между прямыми, L – длина иглы.
Положение случайным образом брошенной на чертеж иглы (рис 2).
Вероятность события – «игла пересекла прямую» – вычисляется по формуле Р(А) = 2*L/(a*). Вероятность Р(А) можно приблизительно определить многократным бросанием иглы. Пусть иглу бросали на чертеж S раз и К раз она упала, пересекая одну из прямых, тогда при достаточно большом S имеем Р(А) = К/S.
Отсюда:  2*L*S/a*k
2*L*S/a*k
Мною сделано 240 бросаний, из них на прямую попали 186 раз. Вычислим число  = 2* 4*240/(4,3*186) = 2,4006. Этот эксперимент мне помогали выполнять ученики нашей школы, но, к сожалению, результатов близких значению Пи получено не было. Значения вычислений были получены в пределах от 2,4 до 3,4.
= 2* 4*240/(4,3*186) = 2,4006. Этот эксперимент мне помогали выполнять ученики нашей школы, но, к сожалению, результатов близких значению Пи получено не было. Значения вычислений были получены в пределах от 2,4 до 3,4.
В чем же сложность вычисления значения числа ? Дело в том, что оно не только иррациональное, то есть, его нельзя выразить в виде дроби p/q, где p –целое, а q – натуральное числа. Такие числа нельзя записать точно, их можно вычислять только методом последовательных приближений, увеличивая число шагов для получения большей точности. Самый простой путь — рассматривать вписанные в окружность правильные многоугольники со все возрастающим числом сторон и вычислять отношение периметра многоугольника к его диаметру. С ростом числа сторон, это отношение стремиться к числу . Именно так в 1593 году Адриан ван Ромен вычислил периметр вписанного правильного многоугольника с 1073741824 (т.е. 230) сторонами и определил 15 знаков . В 1596 году Лудольф ван Цейлен получил 20 знаков, рассчитав вписанный многоугольник с 60·233сторонами. Впоследствии он довел вычисления до 35 знаков.
Бесконечные ряды
В математической литературе я нашел другой путь вычисления — использование формул с бесконечным числом членов. Например:
1) К концу. XIX в., после 20 лет работы, англичанин Вильям Шенкс нашел 707 знаков числа . Однако в 1945 году обнаружено с помощью ЭВМ что Шенкс в своих вычислениях допустил ошибку в 520-м знаке и дальнейшие вычисления оказались неверными. После разработки методов дифференциального и интегрального исчисления было найдено много формул, которые содержат число "пи". Некоторые из этих формул позволяют вычислять "пи" приемами, отличными от метода Архимеда и более рациональными. Так к числу "пи" можно прийти, отыскивая пределы некоторых рядов. Так Г.В. Лейбниц(1646-1716) получил в 1674 году ряд:
Для решения этой задачи я воспользовался языком программирования Turbo Pascal. Сначала я нашел с помощью оператора цикла сумму положительных чисел, а потом сумму отрицательных слагаемых. Затем полученные суммы сложил.
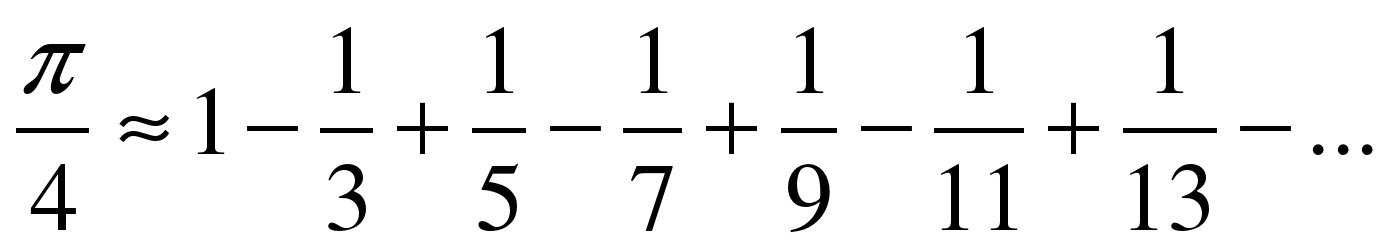
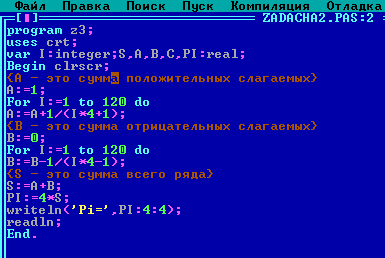
Сумма положительных слагаемых выражается формулой:

Сумма отрицательных слагаемых выражается формулой:

Для проведения более точного вычисления я задавал разное значение параметра цикла, увеличивая его от 10 до 120.
Результаты получились следующие:
n= 10, 3,1892;
n= 20, 3,1660;
n= 30, 3,1580;
n= 40, 3,1539;
n= 50, 3,1515;
n= 60, 3,1499;
n= 70, 3,1487;
n= 80, 3,1478;
n= 90, 3,1471;
n= 120, 3,1457.
Можно заметить, что вычисления с помощью этого ряда дает три верные цифры. Причем, чем больше слагаемых взять, тем точнее получается результат.
2) Вторую формулу для вычисления числа Пи через разложение его в ряд я нашел следующую:
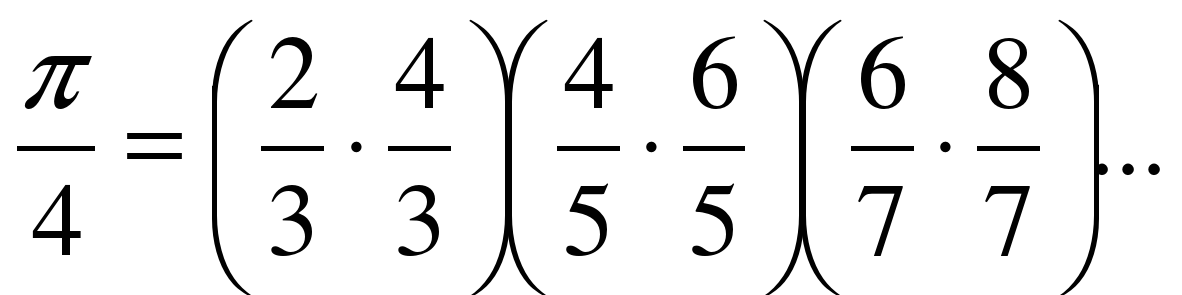
Для вычисления этой формулы начальное значение произведения было задано равным 1, а само произведение вычислялось по формуле:
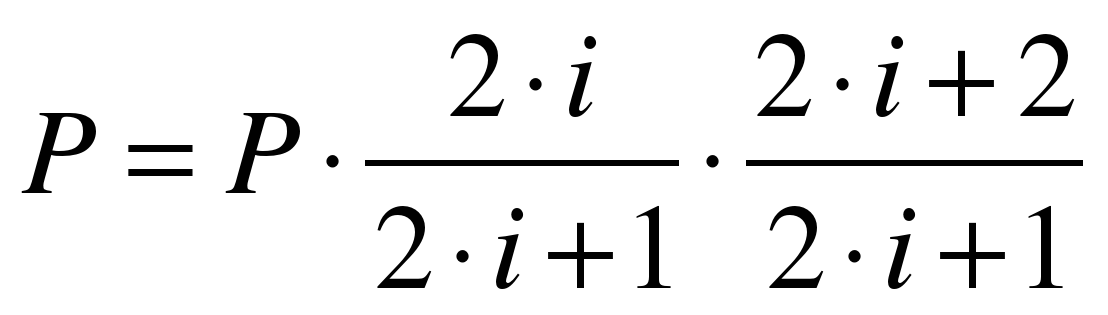
Результаты вычисления:
I= 200; =3, 1455;
I= 300; =3, 1442;
I=400; = 3, 1436;
I= 4000; =3, 1418.
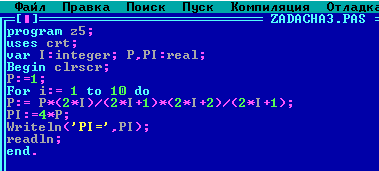
3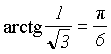 ) Для вычисления "пи" удобнее использовать ряд, получаемый от разложения arctg(x), т.к. и, следовательно:
) Для вычисления "пи" удобнее использовать ряд, получаемый от разложения arctg(x), т.к. и, следовательно:
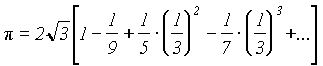
Частичные суммы этого ряда можно вычислять по формуле

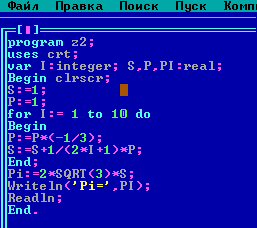
Результаты использования расчетов данного ряда:
I= 10; = 3,14159 ;
I= 40; = 3,14159;
I=100; = 3,14159;
I= 300; = 3,14159;
I= 320; = 3,14159
Современные ЭВМ могут находить приближение числа Пи десятками тысяч верных знаков но, конечно, для практики такие приближения не нужны. За то долгое время, пока человек пытался найти точное значение числа Пи, были предложены различные приближения к его значению.
11 января 2010 француз Фабрис Беллар вычислил число Пи с рекордной точностью. Об этом сообщается на его официальном сайте. Новый рекорд составляет около 2,7 триллиона (2 триллиона 699 миллиардов 999 миллионов 990 тысяч) десятичных знаков. Предыдущее достижение принадлежит японским ученым, которые посчитали константу с точностью до 2,6 триллиона десятичных знаков. Беллар потратил на вычисления около 103 дней.
Все расчеты проводились на домашнем компьютере, стоимость которого лежит в пределах 2000 евро. Для сравнения, предыдущий рекорд был установлен на суперкомпьютере T2K Tsukuba System, у которого ушло на работу около 73 часов. Сначала Пи рассчитывалось в двоичной системе, после чего переводилось в десятичную. На это ушло около 13 дней. В общей сложности для хранения всех цифр требуется 1,1 терабайта дискового пространства.
Подобные вычисления имеют не только прикладное значение. Так, в настоящее время с π связано множество нерешенных задач. Например, известно, что π и e (основание экспоненты) являются трансцендентными числами, то есть не являются корнями никакого многочлена с целыми коэффициентами. При этом, однако, является ли сумма этих двух фундаментальных констант трансцендентным числом или нет — неизвестно до сих пор.
До сих пор не доказано встречаются ли в числе Пи все цифры от 0 до 9 одинаково часто, или какая-то цифра встречается чаще, чем другие.
Мне кажется, что тема очень интересная, изучать ее и экспериментировать вычисление числа Пи можно еще очень долго. Тем более, что вопросов про числа-константы остается много.

 Получите свидетельство
Получите свидетельство Вход
Вход



 a=2R
a=2R – количество «набрызганных» точек, K – количество точек, попавших в круг. Чем больше задать точек N, тем точнее получаются результаты.
– количество «набрызганных» точек, K – количество точек, попавших в круг. Чем больше задать точек N, тем точнее получаются результаты.

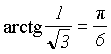 ) Для вычисления "пи" удобнее использовать ряд, получаемый от разложения arctg(x), т.к. и, следовательно:
) Для вычисления "пи" удобнее использовать ряд, получаемый от разложения arctg(x), т.к. и, следовательно: 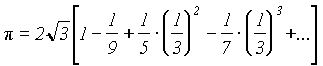











 Знаменитое число ПИ (0.28 MB)
Знаменитое число ПИ (0.28 MB)
 0
0 984
984 59
59 Нравится
0
Нравится
0











