Законы движения планет. Законы Кеплера

Законы движения планет Солнечной системы .

ЗАКОНЫ КЕПЛЕРА

Автор: Александрова З.В., учитель физики и информатики,

2019 г.

МБОУ СОШ №5 пгт Печенга, Мурманская область

В глубокой древности было замечено, что в отличие от звезд, которые неизменно сохраняют свое взаимное расположение в пространстве в течение столетий, планеты описывают среди звезд сложнейшие траектории.

Для объяснения петлеобразного движения планет древнегреческий ученый К. Птоломей (II в.н. э.), считая Землю расположенной в центре Вселенной, предположил, что каждая из планет движется по малому кругу (эпициклу), центр которого равномерно движется по большому кругу, в центре которого находится Земля. Эта концепция получила название птоломеевой или геоцентрической системой мира.

Тихо Браге (1546-1601)

Большую роль в развитии теории движения планет сыграли многолетние наблюдения датского астронома Тихо Браге

Иоганн Кеплер (1571-1630)

Немецкий математик, астроном, оптик и астролог. Открыл законы движения планет.

Наблюдения Тихо Браге были обработаны знаменитым астрономом Игонном Кеплером. Изучая движение Марса по наблюдениям Тихо Браге и используя расчёты Коперника стал подбирать для Марса подходящую форму орбиты

Иоганн Кеплер

К началу XVII столетия большинство ученых убедились в справедливости гелиоцентрической системы мира. Иоганн Кеплер, обработав результаты многочисленных наблюдений, проведенных Тихо Браге (которого называют «человеком, измерившим небо»), получил законы движения планет вокруг Солнца.

Кеплер Иоганн  (1571–1630) – немецкий ученый, один из творцов небесной механики. Работы в области астрономии, механики, математики. Используя наблюдения Тихо Браге и свои собственные, открыл законы движения планет (три закона Кеплера). Известен как конструктор телескопа (так называемая зрительная труба Кеплера, состоящая из двух двояковыпуклых линз).

Иоганн Кеплер (1571-1630) -

немецкий математик, астроном, оптик и астролог. Открыл законы движения планет.

Памятник Кеплеру и Тихо Браге. Прага .

Мемориал Кеплеру

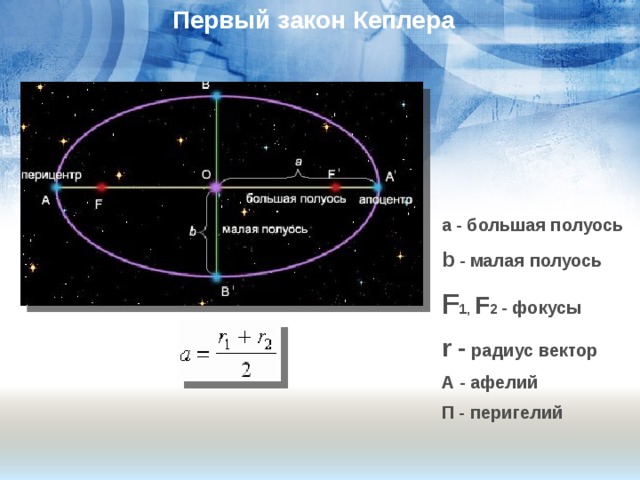
Первый закон Кеплера

1-ый закон: Каждая планета Солнечной системы обращается по эллипсу , в одном из фокусов которого находится Солнце .

Характеристики эллипса

Кеплер предположил, что орбита Марса эллиптическая, и увидел, что эта кривая хорошо описывает наблюдения, если Солнце поместить в один из фокусов эллипса. Затем Кеплер предположил, что все планеты движутся по эллипсам, в фокусе которых находится Солнце. А орбиту Луны он описал эллипсом, в фокусе которого расположена Земля.

Первый закон Кеплера

а - большая полуось

b - малая полуось

F 1, F 2 - фокусы

r - радиус вектор

А - афелий

П - перигелий

1 - гиперболой . с - расстояние от центра до фокуса, а – большая полуось. " width="640"

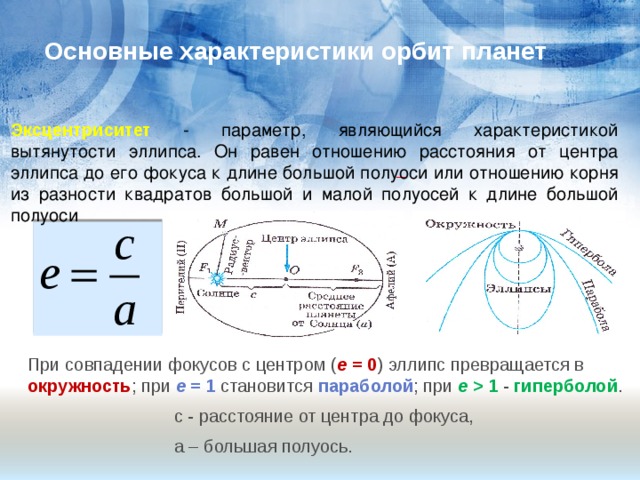
Основные характеристики орбит планет

Эксцентриситет - параметр, являющийся характеристикой вытянутости эллипса. Он равен отношению расстояния от центра эллипса до его фокуса к длине большой полуоси или отношению корня из разности квадратов большой и малой полуосей к длине большой полуоси

_

При совпадении фокусов с центром ( е = 0 ) эллипс превращается в окружность ; при е = 1 становится параболой ; при е 1 - гиперболой .

с - расстояние от центра до фокуса,

а – большая полуось.

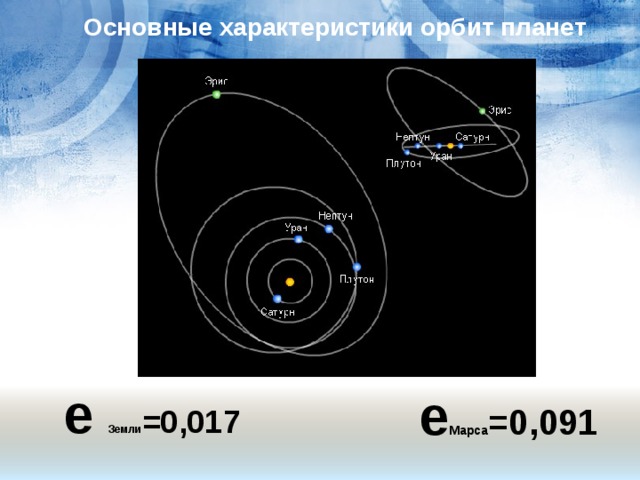
Основные характеристики орбит планет

е Земли =0,017

е Марса =0,091

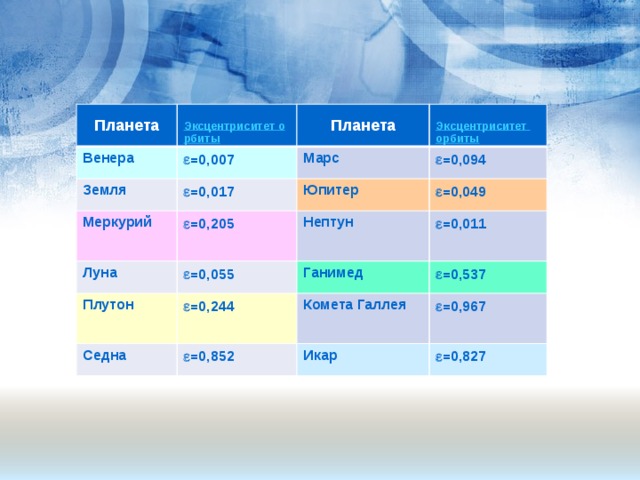
Планета

Венера

 =0,007

Земля

Планета

Марс

 =0,017

Меркурий

 =0,205

 =0,094

Луна

Юпитер

Нептун

 =0,049

Плутон

 =0,055

 =0,244

 =0,011

Ганимед

Седна

 =0,537

Комета Галлея

 =0,852

 =0,967

Икар

 =0,827

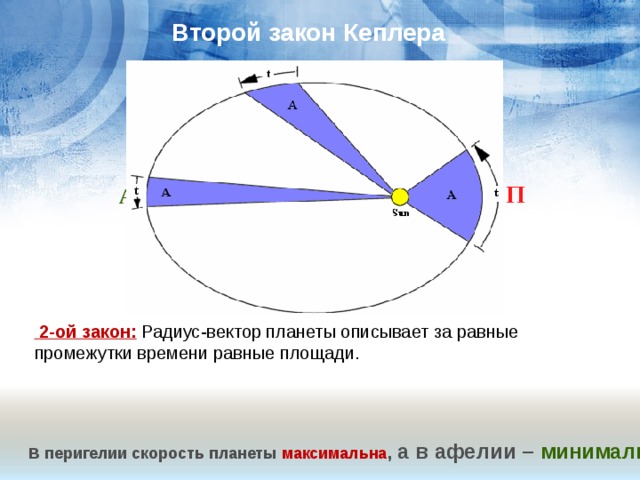
Второй закон Кеплера

S 2

П

А

S 1

S 3

2-ой закон: Радиус-вектор планеты описывает за равные промежутки времени равные площади.

В перигелии скорость планеты максимальна , а в афелии – минимальна.

Планеты по орбите движутся не равномерно: в перигелии скорость планеты наибольшая, в афелии - наименьшая.

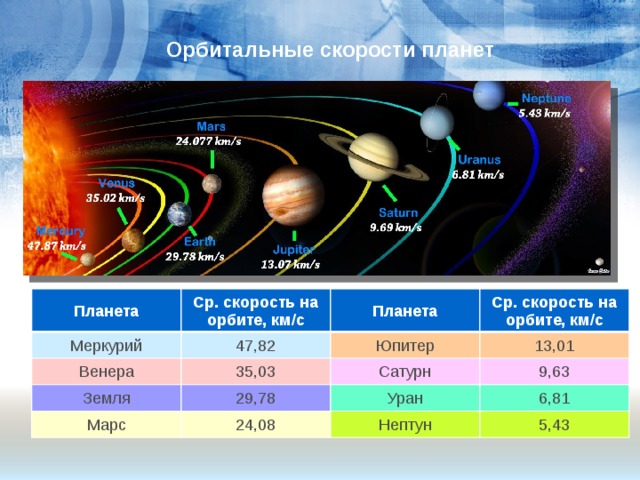
Орбитальные скорости планет

Планета

Ср. скорость на орбите, км/с

Меркурий

Венера

Планета

47,82

Земля

Ср. скорость на орбите, км/с

Юпитер

35,03

Марс

Сатурн

29,78

13,01

Уран

24,08

9,63

6,81

Нептун

5,43

Большая полуось земной орбиты принята

за астрономическую единицу расстояний:

1 а. е. = 149000000000 м

Звездный период Земли

1 год = 365 суток

Третий закон Кеплера

3-й закон: Квадраты периодов обращения планет относятся как кубы больших полуосей их орбит.

Уточненный

закон Кеплера

  Обобщенный третий закон Кеплера справедлив для любых двух независимых систем, каждая из которых состоит из центрального тела и спутников, взаимодействующих по закону всемирного тяготения.

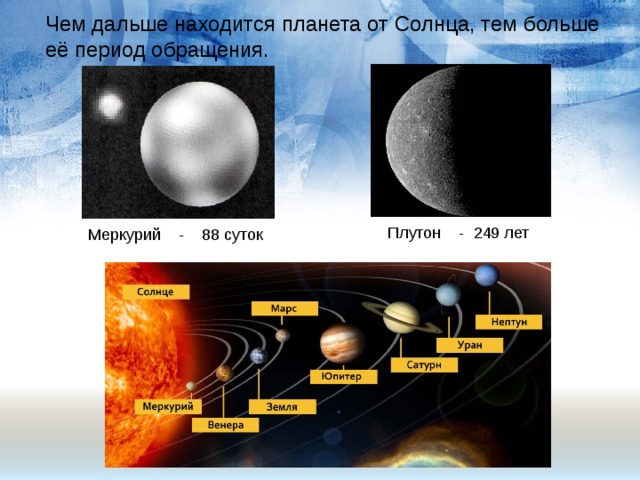
Чем дальше находится планета от Солнца, тем больше её период обращения.

Плутон - 249 лет

Меркурий - 88 суток

Задача 1.

Определите среднее расстояние от Юпитера до Солнца, если известно, что его звездный период обращения вокруг Солнца равен 11,86 года.

Дано :

Решение:

Т= 11,86 года

Т З =1 год

а з =1 а.е.

а – ?

Ответ: 5,2 а.е.

Задача 2.

Определите массу Сатурна (в массах Земли), если известно, что спутник Сатурна Титан отстоит от него на расстоянии 1220 тыс. км и обращается с периодом 16 суток.

Решение:

Дано:

а=1220 ·10 3 км

Т=16 суток

а л =384·10 3 км

Т л =27,3 суток

М З =1

М С – ?

Ответ:

Задача 3.

Рассчитайте время полета по полуэллиптической орбите до Марса.

Дано:

Решение:

а м =1,52 а.е.

Т З =1 год

а з =1 а.е.

t – ?

Ответ: 0,71 года