Закон всемирного тяготения

Закон всемирного тяготения. Гравитационное поле.

Закон всемирного тяготения позволяет описывать не только падение тел на землю, но и движение планет, звезд, приливы, отливы и множество других универсальных явлений, которые протекают в природе.

Если Земля сообщает любому телу, находящемуся на ее поверхности, ускорение свободного падения g, которое, как мы знаем, по модулю равно g = 9,8  , то Луне притяжение Земли сообщает центростремительное ускорение.

Радиус Земли (он нам понадобится в расчетах) R₃ = 6370 км, орбиты Луны R_Л = 384000 км, период обращения Луны вокруг Земли, так называемый лунный месяц Т = 27,3 суток.

Ньютон предположил, что сила, с которой Земля притягивает те или иные объекты, зависит от расстояния между объектом и центром Земли. Известно, что расстояние от Луны до центра Земли примерно в 60 раз больше чем радиус Земли, т. е. расстояние от любого тела находящегося на поверхности Земли.

А во сколько же раз отличается ускорение, приобретаемое телами в результате такого притяжения? Для начала рассчитаем ускорение, которое приобретает Луна в результате своего притяжения Землей. Ускорение, которым обладает любое тело, находящееся на поверхности Земли, вы и так хорошо знаете, это ускорение свободного падения.

Переходим к расчетам.

Центростремительное ускорение Луны, вызванное притяжением Земли, может быть рассчитано по формуле:

Угловая скорость нам не известна, но мы прекрасно знаем, что угловая скорость связана с периодом вращения таким соотношением:

Получим:

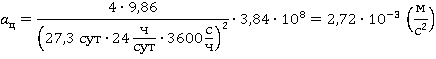
Само по себе это значение может ничего нам не говорить, но сравним его с величиной ускорения свободного падения g = 9,8   и тоже вызванной земным притяжением. Итак, находим отношение:

Почему выделяем именно 60²? Дело в том, что Луна по отношению к поверхности Земли расположена как раз на расстоянии приблизительно в 60 раз больше, чем сам радиус Земли.

Исходя из наших расчетов, мы с вами получаем, что сила, с которой Земля притягивает Луну, обратно пропорциональна квадрату расстояния между центрами этих объектов:

Кроме этого, из второго закона Ньютона мы знаем, что сила прямо пропорциональна массе объекта. Т. е. в данном случае сила прямо пропорциональна массе Луны или другого небесного тела:

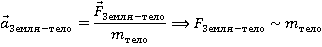
Из третьего закона Ньютона мы знаем, что сила действия вызывает аналогичное противодействие, направленное в противоположную сторону, значит, сила взаимодействия между Землей и Луной будет пропорциональна не только массе Луны, но и массе Земли тоже:

Объединяя все это в одну пропорциональность, мы можем получить, что сила, с которой взаимодействуют Земля и Луна, пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними:

А если обобщать и говорить не только о Земле и Луне, то запишем аналогичную пропорциональность, но уже для двух произвольных масс. Итак, сила взаимодействия между ними пропорциональна произведению этих масс и обратно пропорциональна квадрату расстояния между этими телами:

Если же перейти к строгому равенству, то мы получаем ту самую формулировку, которая впервые появилась в знаменитом труде Ньютона «Математические начала натуральной философии» (1687) и носит название закона всемирного тяготения.

Закон всемирного тяготения устанавливает, что все материальные объекты притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.

Сила F, с которой частица с массой  m  притягивается к частице, имеющей массу  M  и находящейся на расстоянии r, описывается уравнением

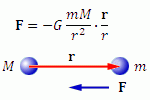
Здесь  r  – вектор, направленный в сторону частицы с массой  m. Вектор     представляет собой единичный вектор в направлении  r, а коэффициент  G  называется гравитационной постоянной.

Знак минус означает, что сила  F  является силой притяжения и действует в направлении, противоположном направлению вектора  r.

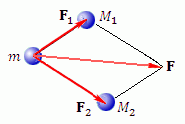
      Если имеется несколько центров притяжения, то каждый из них притягивает к себе частицу m с силой, определяемой законом всемирного тяготения, а результирующая сила равна векторной сумме сил притяжения.

,

       Энергия потенциального взаимодействия двух тел массами  m  и  M, находящимися на расстоянии  r  друг от друга, описывается уравнением

.

     Тело с массой  M  может рассматриваться как источник векторного поля  E  гравитационных сил притяжения, действующих на любые другие тела, обладающие массой. Это поле существует в каждой точке пространства и определяется равенством .

Иначе говоря, гравитационное поле  E  определяет силу, действующую со стороны поля на частицу единичной массы, то есть представляет собой векторное поле, являющееся силовой характеристикой распределения источников притяжения.

Каждое телом массой М создает вокруг себя поле, если же в некоторую точку этого поля поместить пробное тело массой m, то поле действует на пробную массу с некоторой силой F, зависящей от свойств поля в этой точке и от величины массы пробного тела. В свою очередь, пробное тело создает вокруг себя поле, которое действует на тело с массой M.

Таким образом гравитационное поле материально, и оно характеризует изменение физических и геометрических свойств пространства вблизи массивных тел.

Гравитационное поле существует вне зависимости от нашего сознания и может быть обнаружено по его воздействию на физические приборы, на пример на измерительные приборы.

Гравитационное поле является одним из видов материи.

Коэффициент пропорциональности G в этом уравнении называется гравитационной постоянной. Численно она равна модулю силы тяготения, действующей на точечное тело единичной массы со стороны другого такого же тела, находящегося от него на единичном расстоянии.

     Аналогично, потенциал гравитационного поля определяется как потенциальная энергия частицы единичной массы,

,

и представляет собой скалярное гравитационное поле.

В единицах СИ рекомендованное на 2014 год значение:

   м3·с−2·кг−1, или Н·м²·кг−2.

Гравитационная постоянная присутствует в большинстве формул, связанных с гравитационным взаимодействием.

В частности, она входит в уравнения общей теории относительности и ковариантной теории гравитации, а также используется в формулах при определении поля гравитационного кручения. Значение гравитационной постоянной и её константа взаимодействия таковы, что гравитационное взаимодействие между элементарными частицами на много порядков меньше, чем слабое, электромагнитное или сильное взаимодействия.

Гравитационная постоянная фигурирует в современном законе всемирного тяготения, однако отсутствовала у Ньютона и в работах других ученых вплоть до начала XIX века.