Задача к теме "Графы".Теория графов пока не нашла своего отражения в учебниках математики. Отличаясь простотой теоретических сведений, наглядностью и доступностью, теория графов может с пользой найти отражение на самом раннем этапе обучения школьников. Эта теория может найти своё применение в таких областях математики, как математическая логика, комбинаторика и др.В повседневной жизни все больше применение находят графические иллюстрации, геометрические представления и другие приемы и методы наглядности.
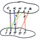
Задача: В велогонках приняли участие пять школьников . После гонок четыре болельщика заявили, что , а) Сережа занял II место, а Коля-III; б) Надя заняла III место, а Толя-V; в) Толя занял I место, а Надя-II; г) Сережа занял второе место, а Ваня-IV. Зная, что одно из показаний каждого болельщика верное, а другое ложное, найдите правильное распределение мест . Решение: Предложение, что Сережа занял второе место, верно (рис.1). Высказывания первого болельщика обозначим синей линией, второго- красными, третьего- зелеными, четвертого- желтыми. Читаем ответ: Толя-I место, Сережа-II место, Надя-III, Ваня может занять только V место, тогда Коля-IV. Предположим, высказывание, что Коля занял 3-е место, верно (рис.2).Читаем: Надя- II место, Коля- III, Ваня-IV, Толя-V, остается Сережа-I место. Итак, задача имеет два решения.
рис.1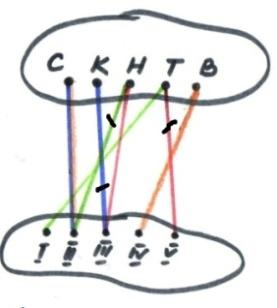 рис.2
рис.2 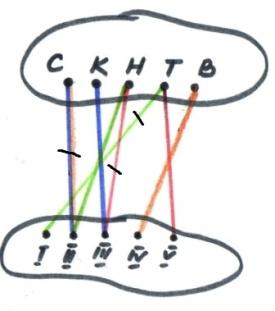
Задача к теме "Логика". Значение логических задач в обучении учащихся трудно переоценить. Они вырабатывают умения устанавливать связи между объектами, наблюдательность, настойчивость в преодолении трудностей. Шестиклассникам логические задачи окажут большую услугу в последующем обучении, особенно при изучении геометрии, когда учащимся придется доказывать теоремы, представляющие цепочку логических рассуждений, сводящих доказываемую теорему к ранее доказываемым теоремам и аксиомам. Школьникам необходимо прививать вкус к логическим рассуждениям. Недаром говорят, что "математика дисциплинирует ум, приучает к логическому мышлению."
Задача (шутка): Два города А и В расположены рядом. Жители обоих городов часто навещают друг друга. Известно, что все жители города А всегда говорят только правду, а жители города В всегда лгут. Какой вопрос следует задать жителю, которого вы встречаете в одном из городов ( вы не знаете, в каком), чтобы по его ответу "да" или "нет" можно было сразу же определить, в каком городе вы находитесь? Решение: Следует задать вопрос:"Вы живете в этом городе?" Ответ "да"-независимо от того, кто отвечает,- житель города А или житель города В означает, что вы находитесь в городе А. Ответ "нет" при любых условиях будет означать, что вы находитесь в городе В.
Задача к теме "Делимость".Есть много интересных задач, где используются признаки делимости, так же можно доказывать некоторые математические утверждения. Для эффективного развития логического мышления можно и нужно решать различные задачи.
Задача: Докажите, что из любых 11 чисел всегда можно выбрать два таких числа, разность которых кратна 10. Решение: Среди любых 11 чисел всегда имеются по крайней мере два таких числа, которые оканчиваются одной и той же цифрой, а значит, разность этих двух чисел оканчивается нулем, т.е кратна 10.
Задача: Найдите каждый множитель в записи, если известно 1)четырехзначный множитель кратен 5; 2)первый множитель не изменяется, если прочитать его справа налево; 3) произведение кратно 9. 
Решение: а)Первый множитель не может оканчиваться нулем, т.к если он будет оканчиваться нулем, то первая цифра его тоже 0 и число не будет четырехзначным. Значит, последняя и первая цифры 5 и первый множитель имеет вид: 5**5 . б)Произведение первого множителя на каждую цифру второго множителя- четырехзначное число, тогда второй множитель 11.
в)Т.к. произведение кратно 9, а второй множитель 11, то число 5**5 кратно 9, причем обе средние цифры его одинаковы. 5+*+*+5≠27, т.к. сумма цифр должна быть четной. Отсюда следует, что 5+*+*+5=18 и, значит, одинаковые средние цифры 4.
Задача к теме "Комбинаторика". Комбинаторика - это наука, с который каждый встречается в повседневной жизни: сколько способов выбрать 3 дежурных для уборки класса или сколько способов, что бы составить слово из данных букв. Комбинаторная теория является одной из важнейших областей математики, без знания которой не обойтись ни менеджеру, ни программисту, ни другим специалистам. Знать, как проводится решение задач по комбинаторике, значит быть востребованным работником, умеющим решать широкий круг практических задач.
Задача: Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
Решение: В таких числах последняя цифра будет такая же, как и первая, а предпоследняя – как и вторая. Третья цифра будет любой. Это можно представить в виде XYZYX, где Y и Z любые цифры, а X – не ноль. Значит по правилу произведения количество цифр одинаково читающихся как слева направо, так и справа налево равно 9 ∙ 10 ∙ 10 = 900 вариантов.
Задача: Чемпионат, в котором участвуют 16 команд, проводится в два круга (т.е. каждая команда дважды встречается с любой другой). Определить, какое количество встреч следует провести.
Решение: По правилу умножения количество встреч 16•15, но среди этого количества повторяются, например, такие: первая со второй и вторая с первой, поэтому встреч будет (16•15)/2. Так как чемпионат проводится в два круга, то количество встреч (16•15)/2•2=240.
Задача к теме "Чётность". Решения задач с применением четности и нечетности чисел всегда отличались необычайной логической красотой и абсолютной прозрачностью выводов. Они основываются на простейших свойствах арифметических операций (обычно на сложении и вычитании). Знакомство учащихся с такими задачами, выходящих за пределы школьной программы, позволит школьникам более уверенно чувствовать себя при изучении базового материала, а также подготовит их к математической олимпиаде.
Задача: В наборе было 35 гирек массой 1г, 2г,3г, …,35г. Можно ли их разложить на две равные по массе кучки, если гирьки в 1г, 3г и 5г потеряли? Решение: Нет, 17 четных, 18 нечетных – 3 = 15 нечетных слагаемых на 2 не делится.
Задача: В школе 1657 учащихся, причем мальчиков на 204 больше, чем девочек. Доказать, что такого не может быть. Решение: Если девочек х , то всего учеников 2х+204, а это число четное.
Задача к теме "Разрезания". Задачами на разрезание увлекались многие ученые с древнейших времен. Решения многих простых задач на разрезание были найдены еще древними греками и китайцами. В наши дни любители головоломок увлекаются решением задач на разрезание прежде потому, что универсального метода решения таких задач не существует, и каждый, кто берется их решать, может в полной мере проявить свою смекалку, интуицию и способность к творческому мышлению.
Задача: Квадрат 4´4 без угловой клетки разрезать на 3 равные части?
 Ответ:
Ответ: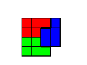
Задача: Разделите каждую из фигур по линиям сетки на четыре одинаковые части, чтобы в каждой части был ровно один кружок.
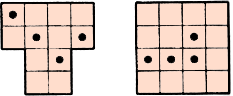 Ответ:
Ответ: 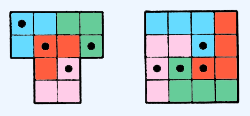

 Получите свидетельство
Получите свидетельство Вход
Вход


 рис.2
рис.2 

 Ответ:
Ответ:
 Ответ:
Ответ: 









 Задачи по математике "Математическая логика" (0.12 MB)
Задачи по математике "Математическая логика" (0.12 MB)
 0
0 2024
2024 169
169 Нравится
0
Нравится
0