Явления интерференции и дифракции

1. Явление интерференции 

Нередки случаи, когда система одновременно участвует в двух или нескольких независимых друг от друга колебаниях. В этих случаях образуется сложное колебательное движение, которое создается путем наложения (сложения) колебаний друг на друга.

Наблюдения за распространением волн на поверхности воды от двух или большего числа источников показывают, что волны проходят одна через другую, совершенно не влияя друг на друга.

Точно так же не влияют друг на друга и звуковые волны: распространение звука от любого источника не испытывает никакого влияния со стороны других звуковых волн, как угодно распространяющихся в это время через те же области среды.

Это объясняется тем, что в пределах упругой деформации сжатие или растяжение тел вдоль одного направления не влияет на их упругие свойства при деформации по любым другим направлениям. Поэтому в каждой точке, которой достигают волны от разных источников, результат действия нескольких волн в любой момент времени равен сумме результатов действия каждой волны в отдельности. Эта закономерность называется принципом суперпозиции.

Принцип суперпозиции: при распространении в линейной среде нескольких волн каждая из них распространяется так, как будто другие волны отсутствуют, а результирующее смещение частиц среды в любой момент времени равно геометрической сумме смещений, которые получают частицы, участвующие в каждом из слагающих волновых процессов.

Интерференция (от лат. inter – взаимно, ferio – ударяю) –  взаимное усиление или ослабление двух (или большего числа) волн при их наложении друг на друга при одновременном распространении в пространстве.

Интерференция волн возможна только при выполнении условия когерентности. Волны называются когерентными, если разность их фаз остается постоянной во времени. Очевидно, что когерентными могут быть лишь волны, имеющие одинаковую частоту. В 1802 г. Томас Юнг при помощи волновой ванны открыл интерференцию.

Проведем следующую демонстрацию: в волновой ванне при помощи вибратора с двумя механически жестко связанными стержнями создадим два точечных источника волн. Вибратор с определенной частотой будет осуществлять возвратно-поступательное движение (в вертикальной плоскости) при помощи электродвигателя. Причем глубина воды в волновой ванне должна превышать создаваемую длину волны λ.

Наблюдения показывают, что в этом случае в волновой ванне возникает особая картина распространения волн – на водной поверхности выделяются полосы, где колебания отсутствуют. Другими словами, волновое поле разделяется интерференционными полосами.

Явление интерференции можно обнаружить в опытах и со звуковыми волнами. Установим два динамических громкоговорителя и подключим их к выходу одного звукового тон-генератора.

Перемещаясь на небольшие расстояния в комнате, на слух можно обнаружить, что в одних точках пространства звучание более громкое, а в других – более тихое. Звуковые волны от двух источников в одних точках пространства усиливают, а в других ослабляют друг друга.

Итак, при наложении в пространстве двух (или нескольких) когерентных волн в разных его точках получается усиление или ослабление результирующей волны в зависимости от соотношения между фазами этих волн. Это явление называется интерференцией волн. Точки пространства, в которых наблюдается максимальное усиление колебаний, называются интерференционными максимумами. Точки пространства, в которых наблюдается максимальное ослабление колебаний, называются интерференционными минимумами.

УПРАВЛЕНИЕ ОБРАЗОВАНИЯ И НАУКИ ЛУГАНСКОЙ ОБЛАСТНОЙ ГОСУДАРСТВЕННОЙ АДМИНИСТРАЦИИ

КУ "ЛУГАНСКАЯ ОБЛАСТНАЯ МАЛАЯ АКАДЕМИЯ НАУК УЧАЩЕЙСЯ МОЛОДЕЖИ"

автор – составитель : А. С. Воронкин

ЯВЛЕНИЯ ИНТЕРФЕРЕНЦИИ И ДИФРАКЦИИ

Луганск - 201 3

Тема V .

ЯВЛЕНИЯ ИНТЕРФЕРЕНЦИИ И ДИФРАКЦИИ

План

5 .1. Явление интерференции

5. 2 . Сложение гармонических колебаний одного направления с близкими частотами. Биения

5.3. Дифракция звуковых волн

5.1 . Явление интерференции

Нередки случаи, когда система одновременно участвует в двух или нескольких независимых друг от друга колебаниях. В этих случаях образуется сложное колебательное движение, которое создается путем наложения (сложения) колебаний друг на друга.

Наблюдения за распространением волн на поверхности воды от двух или большего числа источников показывают, что волны проходят одна через другую, совершенно не влияя друг на друга .

Точно так же не влияют друг на друга и звуковые волны : распространение звука от любого источника не испытывает никакого влияния со стороны других звуковых волн, как угодно распространяющихся в это время через те же области среды.

Принцип суперпозиции ( принцип наложения волн )

Это объясняется тем, что в пределах упругой деформации сжатие или растяжение тел вдоль одного направления не влияет на их упругие свойства при деформации по любым другим направлениям .

Поэтому в каждой точке, которой достигают волны от разных источников, результат действия нескольких волн в любой момент времени равен сумме результатов действия каждой волны в отдельности . Эта закономерность называется принципом суперпозиции.

Принцип суперпозиции: при распространении в линейной среде нескольких волн каждая из них распространяется так, как будто другие волны отсутствуют, а результирующее смещение частиц среды в любой момент времени равно геометрической сумме смещений, которые получают частицы, участвующие в каждом из слагающих волновых процессов.

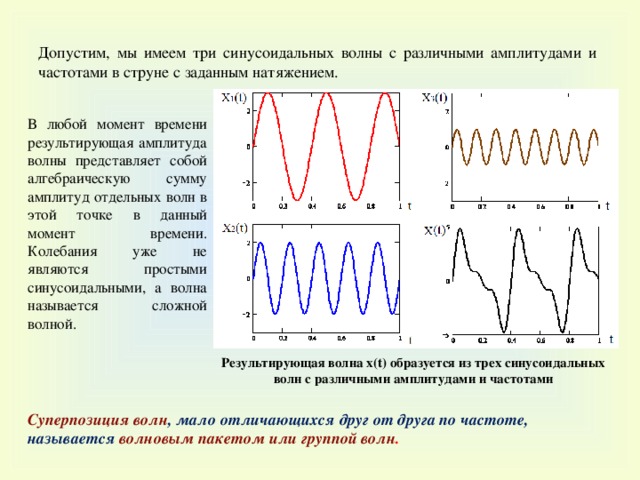
Допустим, мы имеем три синусоидальных волны с различными амплитудами и частотами в струне с заданным натяжением.

В любой момент времени результирующая амплитуда волны представляет собой алгебраическую сумму амплитуд отдельных волн в этой точке в данный момент времени. Колебания уже не являются простыми синусоидальными, а волна называется сложной волной.

Результирующая волна x(t) образуется из трех синусоидальных волн с различными амплитудами и частотами

Суперпозиция волн , мало отличающихся друг от друга по частоте, называется волновым пакетом или группой волн .

Интерференция от двух монохроматических источников одинаковой частоты

Интерференция (от лат. i nter – взаимно, ferio – ударяю) – взаимное усиление или ослабление двух (или большего числа) волн при их наложении друг на друга при одновременном распространении в пространстве.

Интерференция волн возможна только при выполнении условия когерентности.

Волны называются когерентными , если разность их фаз остается постоянной во времени. Очевидно, что когерентными могут быть лишь волны, имеющие одинаковую частоту.

В 1802 г. Томас Юнг при помощи волновой ванны открыл интерференцию.

Проведем следующую демонстрацию: в волновой ванне при помощи вибратора с двумя механически жестко связанными стержнями создадим два точечных источника волн . Вибратор с определенной частотой будет осуществлять возвратно-поступательное движение (в вертикальной плоскости) при помощи электродвигателя. Причем глубина воды в волновой ванне должна превышать создаваемую длину волны λ .

Наблюдения показывают, что в этом случае в волновой ванне возникает особая картина распространения волн – на водной поверхности выделяются полосы, где колебания отсутствуют. Другими словами, волновое поле разделяется интерференционными полосами.

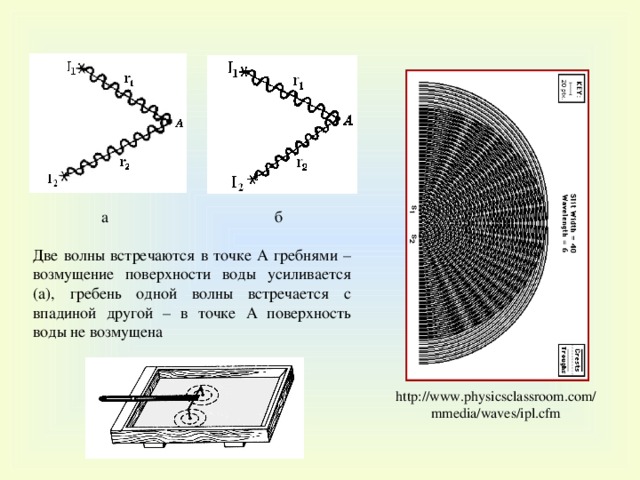
а б

Две волны встречаются в точке А гребнями – возмущение поверхности воды усиливается (а), гребень одной волны встречается с впадиной другой – в точке А поверхность воды не возмущена

http://www.physicsclassroom.com/mmedia/waves/ipl.cfm

Если оба колеблющихся стержня не будут связаны между собой, а будут приводиться в движение двумя вибраторами независимо друг от друга с близкими частотами, то интерференционные полосы начнут перемещаться . При этом они достигают в периодической последовательности положений, которые перед этим занимали соседние полосы.

Явление интерференции можно обнаружить в опытах и со звуковыми волнами . Установим два динамических громкоговорителя и подключим их к выходу одного звукового тон-генератора.

Перемещаясь на небольшие расстояния в комнате, на слух можно обнаружить, что в одних точках пространства звучание более громкое, а в других – более тихое. Звуковые волны от двух источников в одних точках пространства усиливают, а в других ослабляют друг друга.

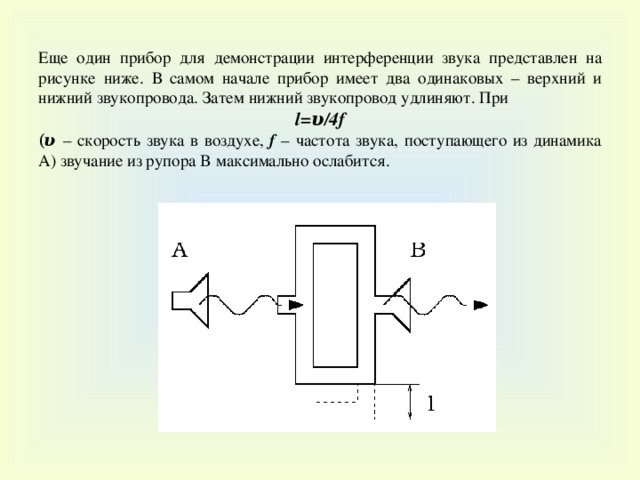
Еще один прибор для демонстрации интерференции звука представлен на рисунке ниже. В самом начале прибор имеет два одинаковых – верхний и нижний звукопровода. Затем нижний звукопровод удлиняют. При

l= υ /4f

( υ – скорость звука в воздухе, f – частота звука, поступающего из динамика A ) звучание из рупора B максимально ослабится.

Условия образования максимумов и минимумов интерференции

Итак, при наложении в пространстве двух (или нескольких) когерентных волн в разных его точках получается усиление или ослабление результирующей волны в зависимости от соотношения между фазами этих волн. Это явление называется интерференцией волн .

Точки пространства, в которых наблюдается максимальное усиление колебаний, называются интерференционными максимумами .

Точки пространства, в которых наблюдается максимальное ослабление колебаний, называются интерференционными минимумами .

I 1 и I 2 – когерентные источники ,

А – точка наблюдения ,

r 1 , r 2 – расстояния, проходимые волнами от источников до точки наблюдения ,

∆ r - называется геометрической разностью хода .

Если на разности хода двух когерентных волн до некоторой точки укладывается целое число длин волн , то в этой точке наблюдается интерференционный максимум :

где k = 0,1,2,3…

Если укладывается нечетное число полуволн , то наблюдается интерференционный минимум :

где k = 0,1,2,3…

Указанные точки образуют два семейства гипербол , причем между каждой парой гипербол, соответствующих точкам с максимальной амплитудой колебаний, находится гипербола из другого семейства, во всех точках которой колебания отсутствуют .

Интерференция и закон сохранения энергии

Куда исчезает энергия двух волн в местах интерференционных минимумов?

Если рассматривать только одно место встречи двух волн, то на такой вопрос нельзя дать правильный ответ. Распространение волн не является совокупностью независимых процессов колебаний в отдельных точках пространства. Сущность волнового процесса заключается в передаче энергии колебаний от одной точки пространства к другой и т. д.

При интерференции волн в местах интерференционных минимумов энергия результирующих колебаний действительно меньше суммы энергий двух интерферирующих волн. Зато в местах интерференционных максимумов энергия результирующих колебаний превышает сумму энергий интерферирующих волн ровно на столько, на сколько уменьшилась энергия в местах интерференционных минимумов.

При интерференции волн энергия колебаний перераспределяется в пространстве, но при этом закон сохранения энергии строго выполняется.

5.2 . Сложение гармонических колебаний одного направления с близкими частотами. Биения

Биения – это колебания с периодически уменьшающейся и увеличивающейся амплитудой, возникающие при сложении двух колебаний одного направления с близкими, но не кратными частотами .

Частота изменения амплитуды суммарного сигнала равна разности частот двух исходных сигналов.

Сложим два гармонических колебания с равными амплитудами и начальными фазами равными нулю, учитывая, что Δω

Получившееся выражение, является произведением двух колебаний и описывает гармоническое колебание с частотой ω и амплитудой x б , изменяющейся по периодическому закону

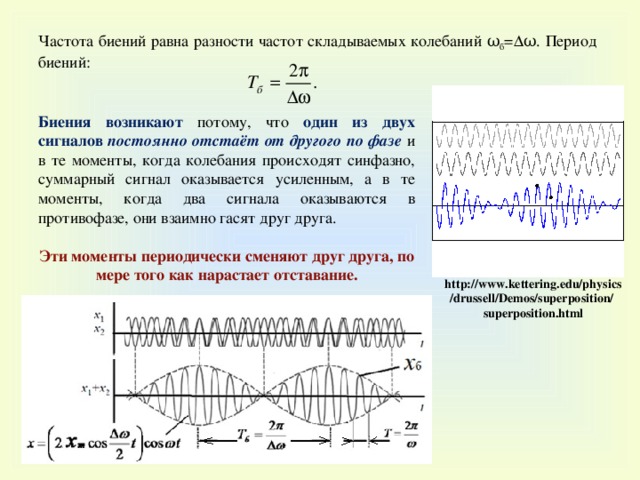
Частота биений равна разности частот складываемых колебаний ω б =Δω. Период биений :

Биения возникают потому, что один из двух сигналов постоянно отстаёт от другого по фазе и в те моменты, когда колебания происходят синфазно, суммарный сигнал оказывается усиленным, а в те моменты, когда два сигнала оказываются в противофазе, они взаимно гасят друг друга.

Эти моменты периодически сменяют друг друга, по мере того как нарастает отставание.

http://www.kettering.edu/physics/drussell/Demos/superposition/ superposition.html

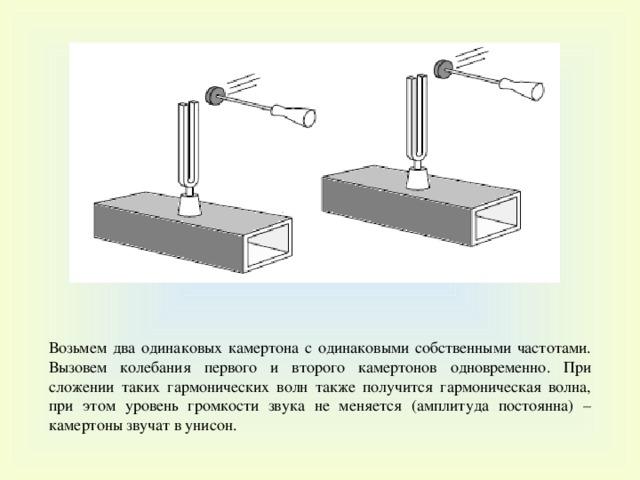
Возьмем два одинаковых камертона с одинаковыми собственными частотами. Вызовем колебания первого и второго камертонов одновременно. При сложении таких гармонических волн также получится гармоническая волна, при этом уровень громкости звука не меняется (амплитуда постоянна) – камертоны звучат в унисон .

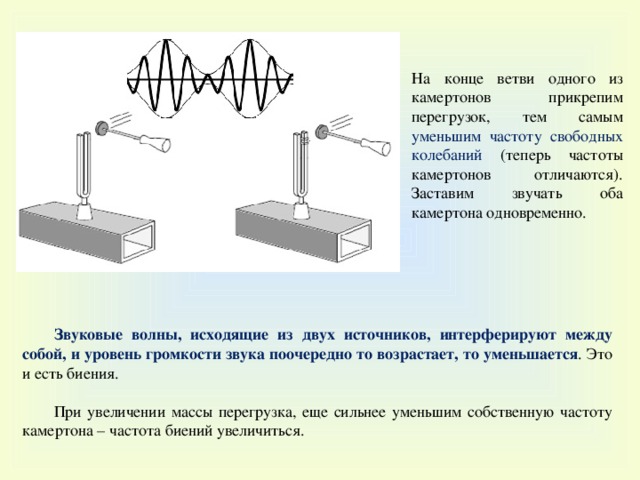
На конце ветви одного из камертонов прикрепим перегрузок, тем самым уменьшим частоту свободных колебаний (теперь частоты камертонов отличаются). Заставим звучать оба камертона одновременно.

Звуковые волны, исходящие из двух источников, интерферируют между собой, и уровень громкости звука поочередно то возрастает, то уменьшается . Это и есть биения.

При увеличении массы перегрузка, еще сильнее уменьшим собственную частоту камертона – частота биений увеличиться.

Подобное явление будем наблюдать и в том случае, когда камертоны заменим двумя электронными генераторами гармонических колебаний. Сигналы одновременно подадим на два различных громкоговорителя.

При “ смешивании ” электрических сигналов и подачи их в один громкоговоритель также услышим биения.

Это указывает на то, что при сложении тонов электрически и акустически – результат один и тот же.

Биения звука можно услышать при настройке струнного музыкального инструмента по камертону (стандартный камертон издает ноту «ля» 1 – ой октавы с частотой 440 Гц). Если частота струны незначительно отличается от частоты камертона, то слышно, что звук пульсирует. Струну подтягивают или ослабляют так, чтобы частота биений уменьшалась. При совпадении высоты звука с эталонным биения полностью исчезают.

Наличием биений также объясняется дребезжащий звук расстроенного фортепиано .

Высокие звуки в этом инструменте излучаются не одной струной, а несколькими, одновременно звучащими в унисон. Если какая-то струна колеблется не с той частотой, что остальные, то появляются биения, которые слушатели воспринимают как дребезжание.

5 . 3. Дифракция волн

Если на пути распространения волны встречается какое-либо тело, то это приводит к появлению эффекта огибания волнами препятствия. Такое явление в физике называется дифракцией . Дифракция волн происходит при их встрече с преградой любой формы.

Степень огибания зависит от соотношения между длиной волны и размерами препятствия или отверстия.

Пусть на поверхности воды распространяется плоская волна, созданная пластиной, закрепленной на электромагнитном вибраторе. На пути этой волны находится преграда с щелью, размер которой a сравним с длиной волны λ (т.е. a = λ ).

Волна, дошедшая до преграды, отразится от нее, а отверстие в преграде будет служить источником колебаний, которые распространяются по другую сторону преграды.

Дифракция круговой волны на узкой щели в стенке

За отверстием независимо от формы исходной волны будут распространяться полукольцевые волны (щель как будто сама является источником колебаний).

Увеличение размера отверстия в преграде на пути волны

Чем больше размеры отверстия в преграде на пути волны, тем меньшие отклонения от прямолинейного направления распространения будут испытывать волны .

Дифракция звуковых волн

Для наблюдения дифракции звуковых волн подключим громкоговоритель к выходу звукового генератора и поставим на пути распространения звуковых волн экран из материала, поглощающего звуковые волны. Передвигая за экраном микрофон, можно обнаружить, что звуковые волны регистрируются и за краем экрана. Изменяя частоту звуковых колебаний и тем самым длину звуковых волн, можно установить, что явление дифракции становится более заметным при увеличении длины волны.

Если размеры препятствия намного больше длины волны, то звук отражается, а позади препятствия формируется зона акустической тени .

Однако п ри достаточно больших расстояниях между источником волн, преградой и местом наблюдения волн дифракционные явления могут иметь место и при больших размерах отверстия или преграды.

Почему при распространении звуки низкой частоты преодолевают большие расстояния, нежели высокие ?

Объясняется дифракцией волн

Как известно, человеческое ухо воспринимает упругие волны в интервале частот от 20 Гц до 20 кГц. Этот интервал в воздухе соответствует следующим длинам волн .

Длина волны на частоте 20 кГц :

м.

м.

Длина волны на частоте 20 Гц :

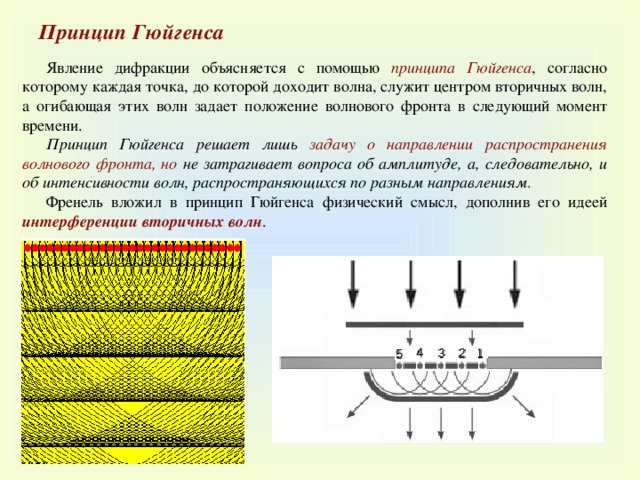
Принцип Гюйгенса

Явление дифракции объясняется с помощью принципа Гюйгенса , согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени.

Принцип Гюйгенса решает лишь задачу о направлении распространения волнового фронта, но не затрагивает вопроса об амплитуде, а, следовательно, и об интенсивности волн, распространяющихся по разным направлениям .

Френель вложил в принцип Гюйгенса физический смысл, дополнив его идеей интерференции вторичных волн .

Демонстрация принципа Гюйгенса-Френеля

Волновая ванна наполняется водой и делится поперечной стенкой на две части. В стенке делается несколько узких отверстий.

При ритмичном колебании пластинки, расположенной параллельно стенке, создается плоский волновой фронт. Каждую щель можно рассматривать как отдельный источник когерентных колебаний.

Во вторую часть сосуда проходят через отверстия круговые волны (элементарные волны Гюйгенса), интерферирующие от всех источников.

Поверхность компакт-диска представляет собой рельефную спиральную дорожку на поверхности полимера, шаг которой соизмерим с длиной волны видимого света. На такой упорядоченной и мелкоструктурной поверхности должны проявляться дифракционные и интерференционные явления. Это и является причиной радужной окраски бликов компакт-диска, наблюдаемых в белом свете.

Как объяснить тот факт, что звуки, представляющие собой суперпозицию волн разной частоты, резкие вблизи источника излучения, по мере удаления от него становятся более глухими и низкими?

Источники

• Воронкин А.С. Линейные колебания и волны: Введение в акустику : уч. пособ. А. С. Воронкин. – Луганск : СПД Рєзніков В.С., 2012. – 224 с. Арабаджи В. Дифракционная окраска насекомых / В. Арабаджи // Научно-популярный физико-математический журнал «Квант», 1991. – №2. – С.18–19. Духовнер А. Об интерференции, дельфинах и летучих мышах / А. Духовнер, А. Решетов, Л. Решетов // Научно-популярный физико-математический журнал «Квант», 1991. – №5. – С. 18–22. Мякишев Г. Я. Физика: Колебания и волны. 11 кл. / Г. Я. Мякишев, А. 3. Синяков. – М. : Дрофа, 2002. – 288 с. Стрелков С. П. Общий курс физики: Механика / С. П. Стрелков. – М. : Наука, 1975, 560 с. Физика. Оптика и волны / под ред. А. С. Ахматова. – М. : Наука, 1973. – Ч. II . – 400 c . Интернет-ресурсы
• Воронкин А.С. Линейные колебания и волны: Введение в акустику : уч. пособ. А. С. Воронкин. – Луганск : СПД Рєзніков В.С., 2012. – 224 с.
• Арабаджи В. Дифракционная окраска насекомых / В. Арабаджи // Научно-популярный физико-математический журнал «Квант», 1991. – №2. – С.18–19.
• Духовнер А. Об интерференции, дельфинах и летучих мышах / А. Духовнер, А. Решетов, Л. Решетов // Научно-популярный физико-математический журнал «Квант», 1991. – №5. – С. 18–22.
• Мякишев Г. Я. Физика: Колебания и волны. 11 кл. / Г. Я. Мякишев, А. 3. Синяков. – М. : Дрофа, 2002. – 288 с.
• Стрелков С. П. Общий курс физики: Механика / С. П. Стрелков. – М. : Наука, 1975, 560 с.
• Физика. Оптика и волны / под ред. А. С. Ахматова. – М. : Наука, 1973. – Ч. II . – 400 c .
• Интернет-ресурсы