«Введение в десятичную дробь»
Методические рекомендации к уроку математики в 5-6 классах
Современное образование в России переживает период перехода в новое качество: социально значимыми становятся способности к самостоятельному выбору, построению или освоению новых способов деятельности. Технология деятельностного метода дает возможность детям вырасти людьми, способными понимать и оценивать информацию; анализировать ее на основе системы теоретических знаний, обладающими навыками к применению этих знаний в нестандартных условиях; способных принимать решения на основе проведенного анализа.
Дидактическая система деятельностного метода обучения состоит в том, что знания не даются учащимся в готовом виде, а организуется их самостоятельное открытие детьми. Такой подход не только обеспечивает высокий уровень математической подготовки, но и развивает мышление, способности, интерес к изучению математики, обеспечивает личностные, метапредметные и предметные результаты образования, соответствующие ФГОС.
При изучении понятия десятичной дроби следует рассмотреть два вопроса:
Десятичная (позиционная) система счета, которая используется для построения десятичной дроби;
Целое-часть.
Название десятичная произошло от правила: единица каждого разряда в 10 раз больше предыдущего (младшего) разряда. Число 10 является основанием системы. Разряд единиц в записи натуральных чисел самый младший, к нему не применяется правило десятичной системы. Если же применить это правило к разряду единиц, то получим дробную часть числа, построенную следующим образом: сначала единица (целое) делится на 10 долей(десятые), затем десятая доля делится еще на 10 долей (сотые) и т.д.
Запись десятичных дробей очень красива, похожа на фонтан, «струи» симметрично бьют из разряда единиц. Мудрая красота: если известно, как построено число слева от разряда единиц, то легко понять и устройство числа справа.
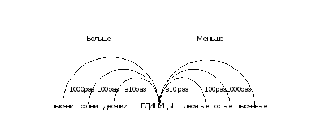
Используя данный подход для построения понятия десятичной дроби, детям нужно выполнить ряд действий, позволяющих вникнуть в сущность понятия.
Предложить детям измерить предмет (отрезок) некоторой произвольной меркой Е, которая целое число раз не укладывается на длине предмета (отрезка).
Чтобы решить проблему, предложить уменьшить мерку в 10 раз, разделив первоначальную мерку на 10 равных частей. Новая мерка равна
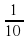 части первой мерки.
части первой мерки.Теперь с помощью новой мерки дети выполняют измерение (остаток при первом измерении предусматривается таким, чтобы новая мерка укладывалась целое число раз).
Записывают результат в таблицу. Например: 2 +
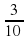 .
.
| тысячи | сотни | десятки | ЕДИНИЦЫ | десятые | сотые | тысячные |
|
|
|
| 2 | 3 |
|
|
Далее предложить измерить другой предмет (отрезок), где новая мерка не укладывается целое число раз.
Предложить детям придумать, как решить проблему. Вероятно, что кто-либо может догадаться снова уменьшить вторую мерку в 10 раз по аналогии с предыдущей задачей (п.2). Третья мерка уже равна
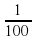
части первоначальной мерки.
Производится измерение и записывается результат. Например, 2+
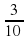 +
+ 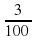
| тысячи | сотни | десятки | ЕДИНИЦЫ | десятые | сотые | тысячные |
|
|
|
| 2 | 3 |
|
|
|
|
|
| 2 | 3 | 3 |
|
С помощью третьей мерки можно выяснить, что
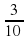 =
= 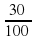 и записать:
и записать:
2 + 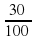 +
+ 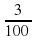 = 2
= 2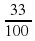 .
.
На данном этапе можно обратить внимание детей на запись измерений в таблице и ввести запись десятичной дроби, предложив отделить целую часть смешанной дроби запятой.
Теперь можно предложить детям самим сформулировать определение десятичной дроби.

 Получите свидетельство
Получите свидетельство Вход
Вход











 «Введение в десятичную дробь» (31.57 KB)
«Введение в десятичную дробь» (31.57 KB)
 0
0 648
648 36
36 Нравится
0
Нравится
0


