Вписанные и центральные углы.

Вписанные углы

СШ 99 г. Минск

9 класс

Определение

• Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется

вписанным.

Чертёж

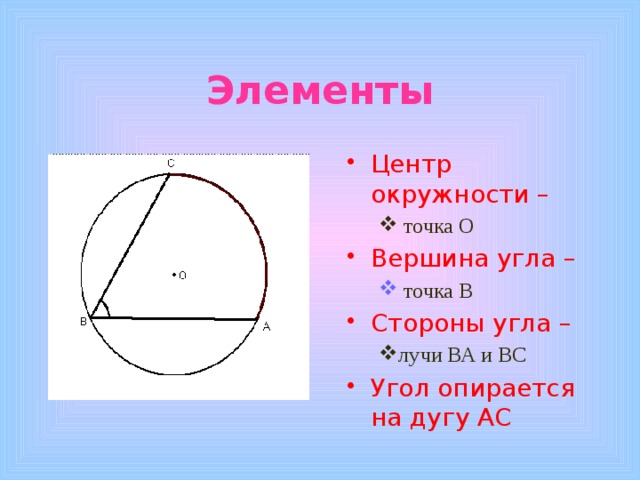
Элементы

• Центр окружности –

• точка О
• точка О
• Вершина угла –

• точка В
• точка В
• Стороны угла –

• лучи ВА и ВС
• лучи ВА и ВС
• Угол опирается на дугу АС

Углы :

• Угол –

• Центральный угол –

• геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
• геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.

• угол с вершиной в центре окружности.
• угол с вершиной в центре окружности.

СВОЙСТВА

• № 1.

• Вписанный угол измеряется половиной дуги, на которую он опирается. Доказательство .
• Вписанный угол измеряется половиной дуги, на которую он опирается. Доказательство .
• № 2. Вписанные углы, опирающиеся на одну и ту же дугу, равны. Докажем .
• Вписанные углы, опирающиеся на одну и ту же дугу, равны. Докажем .
• № 3. Вписанный угол, опирающийся на полуокружность, - прямой. Проверим.
• Вписанный угол, опирающийся на полуокружность, - прямой. Проверим.

Теорема о вписанном угле случай 1-й. Одна из сторон угла проходит через центр окружности.

Дано :

 АВС – вписанный угол

Доказать:

 АВС = ½  АС

Доказательство:

1.  АОВ – равнобедренный,

так как ОВ = ОА = R, значит,  В =  А.

2.  СОА – внешний угол, следовательно,

 СОА =  ОВА +  ОАВ

 СОА = 2  ОВА, значит,

 ОВА = ½  СОА

 СВА = ½  АС. Остальные 2 случая попробуйте доказать дома самостоятельно

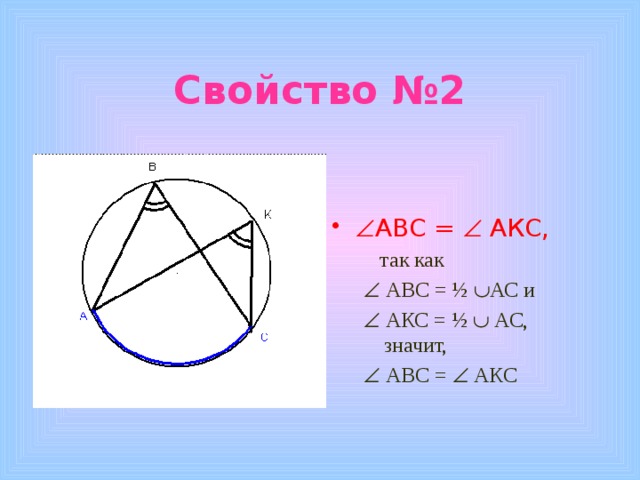
Свойство №2

•  АВС =  АКС,

так как

 АВС = ½  АС и

 АКС = ½  АС, значит,

 АВС =  АКС

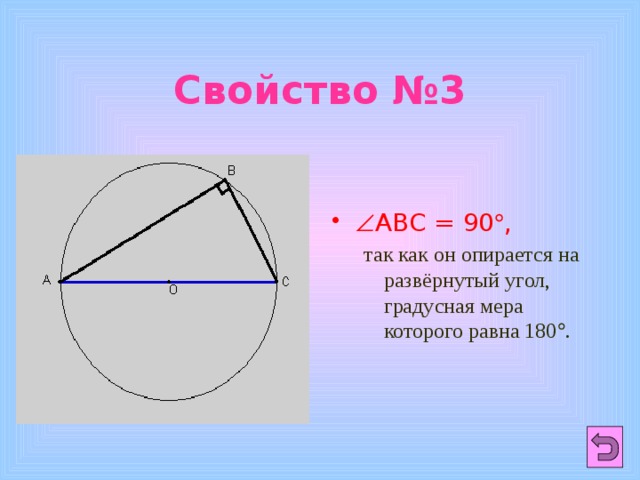
Свойство №3

•  АВС = 90  ,

так как он опирается на развёрнутый угол, градусная мера которого равна 180  .

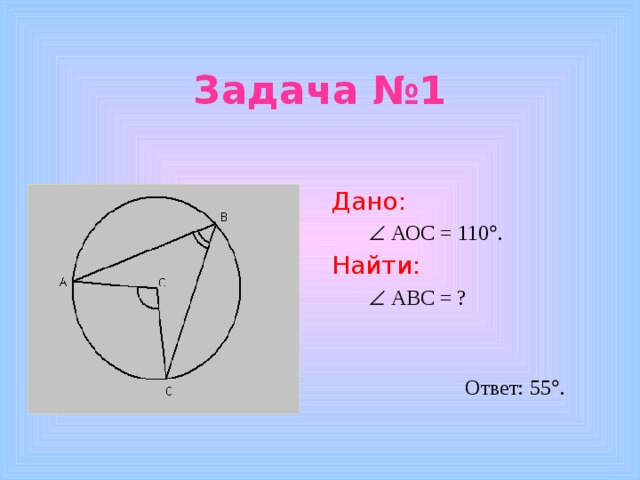
Задача №1

Дано:

 АОС = 110  .

Найти:

 АВС = ?

Ответ: 55  .

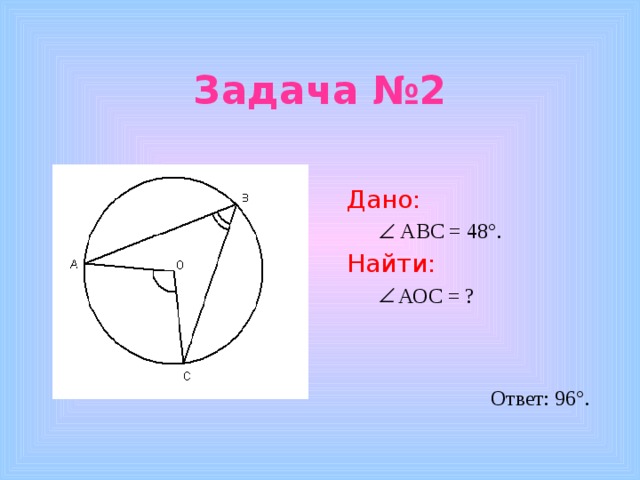
Задача №2

Дано:

 АВС = 48 °.

Найти:

• АОС = ?
• АОС = ?

Ответ: 96°.

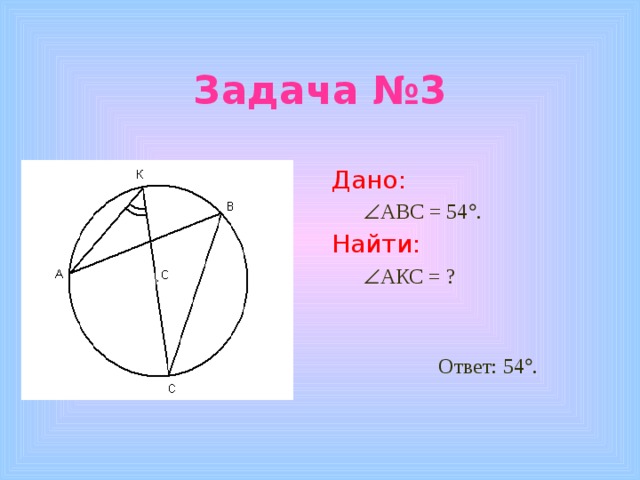
Задача №3

Дано:

 АВС = 54  .

Найти:

 АКС = ?

Ответ: 54  .

Я всё понял !!!