Цели урока:
- вспомнить пройденный материал.
- отработать навыки решения задач по данной теме.
Ход урока.
1. Организационный этап:
- озвучивание темы и целей урока.
2. Повторение теоретического материала.
Теорема о вписанном угле.
Вписанный угол измеряется половиной дуги, на которую опирается.
Следствие 1. Вписанные углы, опирающиеся на одну и туже дугу, равны
Следствие 2. Вписанный угол, опирающийся на полуокружность-прямой.
Теорема о центральном угле:
Центральный угол измеряется градусной мерой дуги, на которую опирается.
3. Решение задач. (отработка навыков)
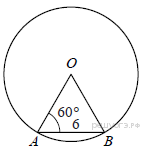
1. Центральный угол AOB опирается на хорду AB длиной 6. При этом угол OAB равен 60°. Найдите радиус окружности.

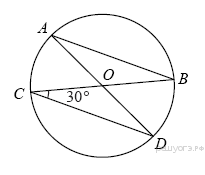
2.В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 30°. Найдите величину угла OAB.
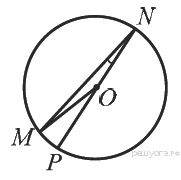
3. Найдите градусную меру ∠MON, если известно,NP — диаметр, а градусная мера ∠MNP равна 18°.
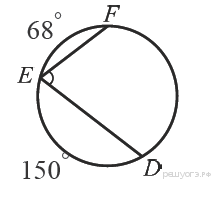
4. Найдите ∠DEF, если градусные меры дуг DE иEF равны 150° и 68° соответственно.
5. Сторона AC треугольника ABC содержит центр описанной около него окружности. Найдите ∠С, если ∠А=75°. Ответ дайте в градусах.
4. Самостоятельная работа.
Вариант 1.
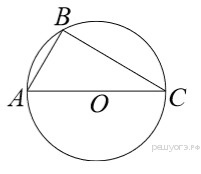
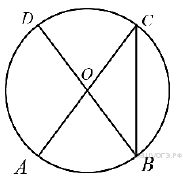
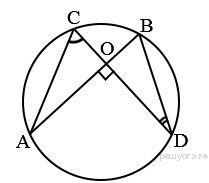
1. В окружности с центром O AC и BD — диаметры. Угол ACB равен 26°. Найдите угол AOD. Ответ дайте в градусах.
2. Точки A и B делят окружность на две дуги, длины которых относятся как 9:11. Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах.
3. Величина центрального угла AOD равна 110°. Найдите величину вписанного угла ACB. Ответ дайте в градусах.
Вариант 2.
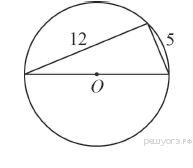
1. Прямоугольный треугольник с катетами 5 см и 12 см вписан в окружность. Чему равен радиус этой окружности?
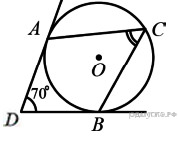
2. В угол величиной 70° вписана окружность, которая касается его сторон в точках A и B. На одной из дуг этой окружности выбрали точку C так, как показано на рисунке. Найдите величину углаACB.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход















 Вписанные и центральные углы (конспект урока) (0.15 MB)
Вписанные и центральные углы (конспект урока) (0.15 MB)
 0
0 2735
2735 479
479 Нравится
0
Нравится
0










