Автор: Асанова Л.К
КГУ ОШ №76
г.Алматы
Алгоритм ұғымы, қасиеттері , түрлері. Алгоритмді құру және орындату.
Алгоритмдер теориясының шығу тарихы. Алгоритмдер теориясының қазіргі күйі.
Алгоритммен келесі зерттеу салалары байланысты:
Алгоритмді талдау. Бұл саланың зерттеу пәніне алгоритм жұмысының сипаттамаларын анықтау жатады. Мысалы: әдетте алгоритмнің жылдам орындалуы талап етіледі (метод оптимизация)
Алгоритмдер теориясы. Бұл салада берілген шамаларды есептеудің тиімді алгоритмдердің болуы/болмау мәселелері қарастырылады.
Алгоритмдерді құру. Бұл сала алгоритмдерді жазуда қолданылатын стандартты әдістер мен тәсілдерді қарастырады. Мыс: Блок-схема.
Алгоритмдер теориясы алгоритмдердің жалпы қасиеттері мен заңдылықтарын, оларды көрсетудің түрлі формальды модельдерін зерттейтін ғылым саласы. Алгоритм ұғымын формальдау арқылы алгоритмдерді тиімділігі бойынша салыстыруға, эквиваленттілігін тексеруге, қолдану салаларын анықтауға болады.
Алгоритмдер теориясының міндеттеріне есептің алгоритмдік шешімі болмауын формальды түрде дәлелдеу, алгоритм күрделілігін асимптотикалық талдау, күрделілік кластарына сәйкес алгоритмдерді жіктеу, алгоритмдер сапасын салыстырмалы түрде бағалаудың өлшемдерін жасау және т.б. жатады.
1930-жылдары жасалған алгоритмдердің формальды модельдері (Пост, Тьюринг, Черч), 1950- жылдары жасалған Колмогоров пен Марковтың модельдері тең , өйткені олар бір біріне мына мағынада эквивалентті: бір модельде шешімі табылған проблемалардың кез келген класы, екінші модельде де шешімі болады.
Қазіргі кезде алгоритмдер теориясының негізінде алынған практикалық ұсыныстар программалаық жүйелерді жасау мен жобалау саласында кеңінен қолданылуда.
Алгоритмдер теориясының шығу тарихы:
Алгоритм ұғымы мен аксиомалық жүйе антика заманынан басталады (Евклид). Алайда алгоритмнің нақты математикалық анықтамасы әлі болған жоқ . XXғ басы Гильберт және оның мектебі арқылы осы ұғымды формализациялады. Кейнс пен оны Гедель жалғастырды және математикалық тұрғыдан кез-келген формуланы автоматты тексеруді құрды (1931).
Алгоритмдер теориясының дамуы алғаш формальды жүйелердің толықсыздығы туралы теораманы 1931 жылы К. Гёдельдің дәлелдеуінен басталды. Осы теоремаға қатысты көптеген математикалық проблемалардың алгоритмдік шешімі болмауы туралы жорамал алгоритм ұғымының стандартталуын қажет етті.
Кейін алгоритм ұғымын стандарттау Тьринг, Черч, Пост т.б. жұмыстарында жалғастырылды. Бұлардың машиналары эквивалентті болды. Алгоритмнің сәтті стандарталған вариантын А.Марков «нормальді алгоритм» ұғымын енгізу арқылы жасады. Гёдель еңбектеріне негізделе отырып С. Клини алдыңғы аталғандарға эквивалентті рекурсивті функция ұғымын енгізді.
Алгоритмдер теориясына Д.Кнут, А.Ахо, Дж. Ульман да өз еңбектерін сіңірді.
Қазіргі кезде алгоритмдер теориясы негізі 3 бағытта дамып келеді:
Алгоритмнің классикалық теориясы – есептерді формальды тілдер терминдерімен беру (формулировка задач) проблемасын зерттеді. Есептерді күрделілік кластары бойынша (P,NP, т.б) классификациясын жасайды, есептердің шешімін табу ұғымын енгізді.
Алгоритмдерді асимтотикалық талдау теориясы. Алгоритмнің , соның ішінде рекурсивті алгоритмдердің, орындалуының уақытының немесе ресурстарының асимтотикалық бағасын алудың тәсілін қарастырады. Асимтотикалық талдау енгізілетін деректер көлемінің өсуіне байланысты алгоритмдердің ресурстарға (мыс: орындалу уақыты) қажеттілігін бағалауға мүмкіндік береді.
Есептеу алгоритмдерін практикалық талдау теориясы. Тиімді алгоритмдерді таңдау әдістемесін жасау, алгоритмдердің сапасын тексерудің практикалық өлшемдерін іздеу, функцияларды интервалдық талдау, күрделіліктің нақты функцияларын алу және т.б. сияқтарды есептерді шешумен шұғылданады.
Қазіргі заманғы алгоритмдер теориясының даму бағыттары мен шешетін негізгі міндеттері:
«Алгоритм» ұғымын формальдау және формальды алгоритмдік жүйелерді (есептеулер модельдерін) зерттеу;
Есептің алгоритмдік шешімі болмайтынын дәлелдеу;
Алгоритмдердің дұрыстығы мен эквиваленттілігін формальды түрде дәлелдеу;
Есептерді классификациялау, күрделілігі бар кластарды анықтау және зерттеу;
Есептің күрделілігінің теориялық төменгі бағасын дәлелдеу;
Тиімді алгоритмдерді құру әдістерін табу;
Итерациялық алгоритмдердің күрделілігін асимптотикалық талдау;
Рекурсивті алгоритмдерді зерттеу және талдау;
Алгоритмдердің қиындығының нақты функцияларын табу;
Алгоритмдердің классификациясын жасау;
Есептер мен алгоримдердің сыйымдылығы бойынша күрделілігін (жад ресурстары бойынша) зерттеу;
Алгоритмдердің ресурстық тиімділігін салыстырмалы түрде бағалаудың критерийлерін және оларды салыстырмалы талдаудың әдістерін жасау.
Алгоритмдер теориясында алынған нәтижелер екі аспектіде: теориялық және практикалық аспектілерде қолданылады.
Теориялық аспект: Есептің алгоритмдік шешімі болатындығын немесе оны шешудің нақты алгоритмі болмайтындығына есепті зерттеу нәтижесінде алгоритмдер теориясының жауап беру мүмкіндігі теориялық аспектіге жатады.
Алгоритмдік шешімі болмайтын есептер Тьюринг машинасын тоқтату есебіне келтіріледі. Ал алгоритмдік шешімі болатын есептер үшін олардың NP-толық есептер класына тиесілі ме екендігі анықталады. Егер тиесілі болса, онда бастапқы деректері үлкен болатын есептердің нақты шешімін алу үшін қанша уақыт кететінін анықтауға немесе оны шешудің жылдам нақты алгоритмі болмайтындығын айтуға мүмкіндік береді.
Практикалық аспект: алгоритмдер теориясының, әсіресе асимптотикалық және практикалық талдаудың әдістері мен әдістемелері келесі мүмкіндіктерді береді:
Берілген есепті шешуге арналған алгоритмдер жиынынан жасалатын программалық жүйедегі олардың ерекшелігін ескеретін тиімді алгоритмді таңдауға мүмкіндік береді.
Күрделілік функциясы арқылы күрделі есептерді шешудің уақыттық бағалауларын алады.
Белгілі уақыт ішінде қандай да бір есептің шешуі болмайтындығына шынайы баға беріледі.
Ақпаратты өңдеу саласындаың маңызды деген есептерін шешудің тиімді алгоримтмдерін құру мен жетілдіру.
Мысалы: алгоритмді жүзеге асыратын программаның орындалу уақытына немесе пайдаланатын минималды жад көлеміне шектеулер қойылғанда түрлі алгоритмдерден таңдау жасалынады; қиындық функциясы арқылы күрделі есептерді шешу уақыты анықталады; берілген уақыт ішінде есепті шешу мүмкін болмайтындығы шынайы бағаланады. Бұл қазіргі кезде криптографиялық әдістер үшін, ақпаратты өңдеу саласында практикалық жағынан маңызды есептерді шешудің тиімді алгоритмдерін жасау мен жетілдіру үшін аса сұранысқа ие болып отыр.
Алгоритм – өңдеудің қарапайым орындалатын тактілерін қолдануға негізделген қандай да бір әдістің нақты және шекті (ақырлы) сипаттамасы. Алгоритм – мүмкін болатын бастапқы деректер класына ортақ есептің шешімін табуға арналған нақты анықталған және орындалатын қарапайым операциялардың ақырлы тізбегінен тұратын, қандай да бір тілде жазылған ақырлы нұсқаулар.
«Алгоритм» ұғымының бірыңғай анықтамасы жоқ. Көптеген анықтамалардың ішінде неғұрлым сәтті берілгені орыс ғалымдары А.Н.Колмогоров пен А.А.Марковтың анықтамалары:
Анықтама 1. (Колмогоров): «Алгоритм – нақты ережелермен қатаң түрде орындалатын, қандай да бір қадамдардан соң қойылған есептің шешіміне әкелетін есептеулердің кез келген жүйесі»
Анықтама 2. (Марков): Алгоритм – өзгертілетін бастапқы деректерден ізделінді нәтижеге әкелетін есептеу процесін анықтайтын нақты ереже.
Бұл анықтамалардан алгоритмге қойылатын келесі ортақ талаптарды атап өтейік:
алгоритм қарапайым орындалатын саны шектеулі ережелерден тұруы тиіс, яғни жазбалардың шектеулі болуы талабын қанағаттандыруы тиіс;
алгоритм шектеулі қадамнан соң есепті шешуі тиіс, яғни әрекеттердің шектеулі болу талабын қанағаттандыруы тиіс;
алгоритм барлық мүмкін болатын бастапқы деректер үшін біреу ғана болуы керек, яғни әмбебаптық талабын қанағаттандыруы тиіс;
алгоритм қойылған есептің дұрыс шешімін табуы керек, яғни дұрыс болу талабын қанағаттандыруы тиіс.
Бұл анықтамаларда әрекетті орындаушы көрсетілуі тиіс және ол орындайтын «қарапайым» операцияларға не жататыны нақтылануы тиіс. Алгоритмді әртүрлі формада бейнелеуге , яғни беруге болады. Кейде әрекеттер ретін графикалық түрде көрсету түсінікті болады, ал оны сөзбен сипаттау қиынға түседі. Сондықтан алгоритмнің нақты формальды анықтамасы туралы ұғым арнайы математикалық конструкцияларды – формальды алгоритмдік жүйелер немесе Пост машинасы, Тьюринг машинасы, Черчтің рекурсивті-есептелінетін функциялары сияқты есептеулер модельдерін енгізумен, бұл формализмнің эквиваленттілігі туралы тезистің айтылуымен және «алгоритм» ұғымымен тікелей байланысты болды.
Z есебінің бастапқы деректерінің жиыны — DZ, aл R — мүмкін болатын нәтижелер жиыны болсын, онда алгоритм DZ R бейнелеуін іске асырады деп айтады. Егер алгоритм тек кейбір dDZ үшін ғана дұрыс нәтиже берсе, онда алгоритм жеке жағдайдың алгоритмі деп аталады. Егер алгоритм барлық dDZ үшін дұрыс нәтиже берсе, онда алгоритм толық алгоритм деп аталады.
Қойылған есептің шешімін арифметикалық амалдарды орындауға келтіретін алгоритмдер сандық алгоритмдер деп аталады.
Д.Кнут «Искусство программирования. Основные алгоритмы» атты кітапта алгоритмнің бес маңызды қасиетін көрсеткен:
1) Ақырлы болуы – алгоритмнің ақырлы қадамынан соң аяқталуы тиіс;
2) Анықтылығы – алгоритмнің әр бір қадамы нақты анықталуы керек.
3) Енгізілетін деректердің болуы – алгоритм жұмысының басына дейін берілетін кірістік деректер болады немесе олар орындалу барысында динамикалық түрде анықталуы мүмкін
4) Шығыстық деректердің болуы – алгоритмде кірістік деректермен белгілі бір байланысы бар немесе бірнеше деректер болады
5) Тиімділік
Алгоритмдер классификациясы. Күрделілілік тұрғысынан алгоритмдердің екі үлкен класы бар қайталауы бар алгоритмдер және рекурсивті алгоритмдер. Бір есепті көптеген алгоритммен шешуге болады. Олардың әрқайсысының жұмысының тиімділігі әртүрлі сипаттаулармен сипатталады. Алгоритмді талдамас бұрын ең алдымен берілген алгоритм есепті дұрыс шешетінін дәлелдеуіміз керек. Егер есепті дұрыс шешпесе тиімділік мәселесінің мәні жоқ. Егер алгоритм қойылған есепті шешсе, оның қаншалықты тиімді екенін қарастыруымыз керек. Сондықтан оның тиімділігінін анықтау үшін алгоритмдерді талдауымыз қажет.
Қайталау алгоритмінің негізінде шартты өрнектер мен цикл жатыр; мұндай алгоритмдерді талдауда циклдын ішінде қолданылатын операция саны мен цикл итерациясының санын бағалау керек. Рекурсивтік алгоритмдер үлкен есепті фрагменттерге бөледі және әрбір фрагменттерді жеке қолдануға мүмкінлік береді. Осындай алгоритмдерді кейде «бөліп алда біле» алгоритмі деп айтайды және оларды қолдану өте тиімді болуы мүмкін. Үлкен есептердікішіге бөлу жолымен шешу үрдісінде үлкен емес, қарапайым және түсінікті алгоритм құрылады. Рекурсивті алгоритмді талдауда есепті бөлімге бөлуге қажетті операцияның санын санау, ірбңр бөлімдегі алгоритмнің орындалуы және есепті толық шешудегі әрбір бөлімнің нәтижесін біріктіру керек. Осы ақпараттарды және неше бөлік екенінің саны, олардың өлшемінен алгоритмнің күрделілігінің рекуррентік қатынасын шығарамыз.
Алгоритмдерді әртүрлі белгілер бойынша жіктеуге болады. Мысалы, жалпы комбинаторлық алгоритмдер, тағы алгоритмдер, максимальды ағынды іздеу алгоритмдері, максимальды жұп сәйкестігін іздеу алгоритмдері, іздеу алгоритмдері, Алгоритмы на строках, жолды іздеу алгоритмдері, Бұтақтармен жұмыс алгоритмдері, сұрыптау алгоритмдері, сығу алгоритмдері, үлестірілген жүйелер алгоритмдері, операциялық жүйелердегі алгоритмдер, тиімділеу алгоритмдері және т.б.
Есептеу моделіне байланысты сандық, логикалық, продукциялық, нейрожелілік, параллель, полиномдық, құмырсқа, генетикалық және т.б. бөлінеді.
Алгоритмдердің тиімділігі
Алгоритм қандай да бір машинада командалардың жинағы түрінде орындалады. Бір есепті орындауға арналған екі немесе бірнеше алгоритмдердің орындалу жылдамдығын салыстыру үшін қолданылатын критерий (өлшем) жүйелік тиімділік деп аталады. Бір компьютерде бірдей деректер жинағымен бұл алгоритмдерді орындату арқылы олардың орындалуына кеткен салыстырмалы уақытты анықтауға болады.Ол үшін ішкі жүйелік сағат қолданылады.
Ішкі жүйелік сағатты қолданып уақытты бағалау бұл бір ғана есептің орындалуына арналған алгоритмдердің әрқайсысының жүйелік тиімділігінің өлшемі болады.
Кейбір алгоритмдердің орындалуында жадқа қойылған шектеулер проблема тудырады. Орындалу барысында ұзақ уақыт сақтау үшін бастапқы көлемді қысу қажет болады. Қандай да бір алгоритм пайдаланатын ішкі жадтың салыстырмалы санының өлшемі — бұл кеңістіктің тиімділігі (space efficiency). Бұл критерий алгоритмді қандай типті компьютер орындай алатынын және алгоритмнің толық жүйелік тиімділігін көрсетеді. Жаңа компьютерлік жүйелердің жадтарының көлемінің ұлғаюна байланысты бұл критерий маңызды болмай қалды.
Үшінші тиімділік критерийі — бұл есептеу тиімділігі (computational efficiency), ол алгоритмнің ішкі құрылымын қарастырады, оның жасалуын және алгоритмде қолданылатын итерациялар мен меншіктеу операторларын салыстыратын тесттердің санын да талдайды. Бұл өлшем типі нақты компьютерге тәуелсіз және бұл критерий алгоритмнің есептелу күрделілігін n-ге, яғни коллекциядағы деректер элементеріне қатысты өлшейді.
Тізімдер мен бұтақтар сияқты коллекциялардың жалпы кластарының деректерін өңдеу үшін алгоритмнің тиімділігінің өлшемі ретінде салыстыру қолданылады.
Әдетте күрделі алгоритмнің ен жаман және ең жақсы жағдайлары үшін әртүрлі есептеу тиімділігі болады, сондықтан әр жағдай үшін есептеу тиімділігін өлшеу үшін, яғни алгоритмнің орындалу уақытының өлшемін анықтау үшін Big-0 нотациясын есептейміз.
Big-0 нотациясы. Алгоритмнің есептеу тиімділігі өңделетін деректердің санымен, яғни алгоритмдегі басты операциялардың санымен анықталады. Бұл операциялар деректің типіне, санына, реттелуіне тәуелді болады. Көп жағдайда сұрыптау алгоритмдерінде (тізімдер мен бұтақтарда) алгоритм тиімділігін өлшемі ретінде салыстыру қолданылады. Ол массив элементтерінің санына тәуелді.
Мысалы массивтегі минимал элементті табу — бұл қарапайым алгоритм, оның негізгі операциясы элементтерді салыстыру. n элементі бар массив үшін алгоритм n-1 салыстыруды қажет етеді, оның тиімділігінің өлшемі n-ге пропорционал. Басқа алгоритмдер күрделі. . Алмастырып салыстыру алгоритмінде жалпы салыстыру саны:
f(n) = (n — 1) + (n — 2) + . . . + 3 + 2 + 1 = n(n — 1)/2 арифметикалық қатармен анықталады. f(n) функциясы салыстырумен ассоциацияланады. Бұл алгоритмнің салыстыру саны n2 болады.
Big-O нотациясын есептеу тиімділігінің өлшемін беру үшін қолданады. Алгоритмнің есептеу күрделілігінің (оны f(n) функциясы немесе салыстырулар саны дейді) реті O(g(n)) -ге тең болады, мысалы алмастырып сұрыптаудың есептеу күрделілігі О(n2) тең. Сызықты алгоритмнің күрделілігі тізімнің размеріне пропорционал болады, оның O(g(n)) - реті О(n) тең.
О(n2) реті бар алгоритмдер квадраттық деп аталады.
Алгоритмдер деректердің бастапқы сұрыпталуына тәуелді болады. Мысалы, реттелген массивтен минимал не максимал элементті табу оңай.
Әдетте Big-О мәні деректер құрылымының алгоритмі үшін көптеген полиномдық, логарифмдік және экспоненциальдық функциялардың арасынан таңдалады. Классикалық деректер құрылымы үшін бұл функциялар алгоритмдердің есептелу күрделілігінің жоғарғы шекарасын береді.
Мына кестеде сұрыптау алгоритмдердегі салыстырулар саны п2 мен п log2 n салыстырылады. Алмастырып сұрыптауға қарағанда О(пlog2n) сұрыптау алгоритмі тиімдірек.
| n | (1/2)n2 | S(n) = n2/2 - n - 2 |
| 10 | 50 | 45 |
| 100 | 5.000 | 4.950 |
| 1000 | 500.000 | 499.500 |
| 5000 | 12.500.000 | 12.497.500 |
| 10000 | 50.000.000 | 49/995.000 |
| | ||
| n | n2 | n log2n |
| 5 | 25 | 11,6 |
| 10 | 100 | 33,2 |
| 100 | 10000 | 664,3 |
| 1000 | 1000000 | 9965,7 |
| 10000 | 100000000 | 132877,1 |
Алгоритмнің күрделілігі. Big-O-бағалау алгоритмнің орындалу уақытының өлшемін (runtime) береді. Әдетте алгоритмнің жақсы және нашар жағдайлар үшін есептеу тиімділіктері әртүрлі , сондықтан әр нақты жағдай үшін Big-О мәні есептеледі.
Егер алгоритм реті —0(1) болса, оның реті коллекциядағы элементтер санына тәуелсіз болады. Бұл алгоритм тұрақты уақыт бірлігі ішінде орындалады, мысалы егер массив соңын көрсететін индекс сақталса, массив элементіне мән меншіктеу реті 0(1) болады.
Алгоритм О(п) сызықты (linear). Оның күрделілігі тізім размеріне пропорционал.
Реті log2n болатын алгоритмдер логарифмдік (logarithmic) деп аталады. Мұндай күрделілік тізімдерді бірнеше рет ішкі тізімдерге 1/2, 1/4, 1/8 етіп бөлгенде туындайды. Мысалы бинарлық бұтақтарда іздеу алгоритмдерінің күрделілігі орташа және нашар жағдайлар үшін O(log2n) болады.
Реті О(п2) болатын алгоритмдер квадраттық (quadratic) деп аталады. Шағын n үшін ғана практикада қолданылады. п екіге артқан сайын алгоритмнің орындалу уақыты 4-ке артады.
Реті О(n3) болатын алгоритмдер өте баяу орындалады, кубтық (cubic) уақытты қажет етеді. п екіге артқан сайын алгоритмнің орындалу уақыты 8 есе артады. Оның мысалына графтарға қолданылатын реті О(п3) болатын Уоршел алгоритмі жатады.
Күрделілігі О(2п) тең алгоритмде экспоненциальды күрделілік (exponential complexity) болады. Өте баяу орындалатындықтан өте аз п үшін қолданылады.
Төмендегі кестеде аталған алгоритмдердің ретінің бағалауы берілген, аз мәнді п үшін кубтық, экспоненциальдық алгоритмдерді қолдану тиімсіз.
Кесте 1 - Алгоритмдер ретін бағалау
| n | lоg2n | n lоg2n | n2 | nэ | 2n |
| 2 | 1 | 2 | 4 | 8 | 4 |
| 4 | 2 | 8 | 16 | 64 | 16 |
| 8 | 3 | 24 | 64 | 512 | 256 |
| 16 | 4 | 64 | 256 | 4096 | 65536 |
| 32 | 5 | 160 | 1024 | 32768 | 4294967296 |
| 128 | 7 | 896 | 16384 | 2097152 | 3.4 х 1038 |
| 1024 | 10 | 10240 | 1048576 | 1073741824 | 1.8 х 10308 |
| 65536 | 16 | 1048576 | 4294967296 | 2.8 х 1014 | қолданбаңыз! |
Алгоритмдерді талдау. Алгоритмнің дұрыстығы, верификациясы және
тиімділігі.
Алгоритмді жобалағанда және дербес жағдайда деректердің құрылымында ағаш кең қолданыста болады. Оқырманды әдебиет жағынан графтың қағидасына көнілін бұрсақ, түйіншек, қабырға, парақ, жұрағат, ұл, сол жұрағат, оң жұрағат, баба, әке, түп, тармақ және басқа да ұғымдарды пайдаланамыз.
Графта қысқаша жолдарды іздестіру
Кіретін деректер:
- Граф G өлше- қабырғалармен(Салмақ жайлы айтқанда қабырңанын ұзындығы деп түсінуге болады, егер геометриялық граф жайлы айтса немесе басқа да қабырғаның санды мінездемелерінде де солай түсінуге болады)
- s бастаманың шыңы (қалған барлық шыңға дейінгі қашықтықты есептейтін шың) Демалыстар: деректерлер
- dist алабы[1.. n], (dist[i] –s шыңынан i шыңына дейінгі қысқа қашықтық).
- up алабы[1..n], (up[i] –s-тен i-ге дейінгі қысқа жолдың соңынының алдындағы шың).
Дейкстраның алгоритмы
Дейкстрының алгоритмыграфқа арнайы қарсылы емес салмақты шыңдары бар есептерді дұрыс есептейді. Егер графта қарсы салмағы бар қабырға болса, бірақ қарсы суммарлы салмақпен цикл болмаған жағдайда, есеп шығу үшін Форд немесе Баллманның алгоритмін пайдалансақ болады. 1. up[1.n] алабын нөлдермен толтыру.
2.Әрбір i шыңына dist[i] кілтінің орнынаdist[i] –максималды мүмкін санды (ол графтағы қысқа жолдардың көбісінің ұзындығынан үлкен болуы қажет; есептеу барысында бұл сан азаяды және соңында s шыңынан i шыңына дейінгі қысқа жолдағы ұзындықпен алмасады).
3. Графтың шыңдарынан басымды кезек ұйымдастыру, кілттің орнына dist [i], i= 1, 2, …, n. аумағын алу.
4. s шыңының кілтін 0-ге ауыстыру.
5. Әлі де кезек бос емес жағдайында6 – 7 операцияларын орындау.
6. Басым кезектен r0 элементін таңдап алу(өшіре);
7.Әрбір r0 шектес r ш 8,9 операциялапын орындау.
8. delta= dist[r] – (dist[r0] + L(r0, r)) аумағын есептеу;
9. Егер delta 0, онда r элементінің кілті dist [r] delta аумағына ке міту және up [r] ескірген аумағын r0 ауыстыру;
Ортақ мәліметтер. Ізденістің ағаштары сөздіктерді берілгеннің абстракты үлгісі ретінде қарауға арналған. тал-шыбықтары үшін сөздіктің тамашасының сияқты деректердің абстракт үлгісінің арнаулы.Басымды кезектер сияқты, олар да көпті ұсынады, бірақ басқа операциялы жиынмен осылай, яғни
• Search - берілген кілтпен элементті іздестіру,
• Minimum –минималды кілтпен элементті іздестіру,
• Maximum –максималды кілтпен элементті іздестіру,
• Predecessor –іздестіру алдыңдағы кілтпен элементті іздестіру,
• Successor–келесі кілтпен элементті іздестіру,
• Insert –өзінің кілт арқылы элементті енгіз,
• Delete –көрсетілген элементті өшіру.
Ізденістің ағашы сөздік ретінде де, басымды кезек ретінде де пайдалануы мүмкін.
Негізгі операций орындалуының уақыты ағаштың биіктігіне пропорционал. Егер әрбір жұпты ағаштын ішкі түйіншегінің екі жұрағаты болады, сонда оның ұзындығы және негізгі операциялардыә орындалу уақыты түйінше санының логарифміне пропорционал. Керісінше, егер ағаш н түйіншектен құралған сызықты шынжырды көрсетсе, бұл уақыт до Θ(n) дейін көбейеді. Байкаусыз ізденіс жұпты ағашы бұл өзі Ο (lоg n) екені белгілі, сондықтан бұл жағдайда Θ(lоg n) негізгіі операцияларды есептеу уақыты болады.
Әрине,пайда болатын iздестiру екiлiк ағашының тәжiрибелерiнде кездейсоқтан алыс бола алады. Алайда, бiз ағаштарды теңдеуiш бойымен арнайы өлшемдер қабылданып n түйiндермен ағаштарын биiктiк болғанын кепiлдiк бере аламыз 0(log n ). Тәсiлдемелердiң бiрлерн мысалды төменде қарап шығамыз. (қызыл-қара ағаштар - АВЛ, дербес жағдайда ағаштар).Сонымен бiрге мәлiметтер үшiн әсiресе ыңғайлы кез келген (дискте) рұқсаты бар екiншi жад сақталған Б-ағаштар қарастырылады. Бұл туралы:
Iздестiру екiлiк ағашының ұсынысы. Iздестiру екiлiк ағашы әрбiр түйiнiне өлшенген элемент сәйкестiкке орнатылған түбiрлiк екiлiк ағашы деп аталады. Әрбiр түйiн x үшiн келесi шартты орындайды.
X түбiрi бар сол ағаш астындағы барлық х түйiндерiнiң салмағынан аз немесе тең, онының оң жақ ағаш астындасының түйiндерiнiң салмағы артық немесе түйiн x салмағына тең.
Келесi түрдiң түйiндерiмен мұндай ағаш өкiлдiк етедi
Node = (element, key, left, right, parent)
T ағашқа рұқсат сiлтеме root көмегiмен жүзеге асырылады.
Екiлiк iздестiру ағашымен операциясы. Көрсетемiз, екiлiк iздестiру ағаштары операция Search, Minimum, Maximum, Successor және Predecessor уақытқа орындауға мүмкiндiк береді (h ), ағаштың биiктiгi h.
1. (Search ) iздестiру. Iздестiрудiң процедурасы k және x iздестiрудi iстелетiн ағаш астынданың түбiрiне көрсеткiш кiре берiске iзделiп отырған кiлт алады. Ол (егер болса) k немесе (егер мұндай шың жоқ жағдайда) nil кiлтпен шыңға көрсеткiштi қайтарады.
Procedure Search (x, k);
begin
if(x = nil) or (k = key [x]) then Return x;
if(k then Return Search (left[x], k) else
Return Search (right[x], k)
end.
Бiз iздестiрудiң процессiнде түбiрден қозғаламыз, кілтті k кiлтпен салыстыра, x ағымдағы шың сақталған қозғаймыз. Егер ол тең болса, iздестiру аяқталады. Егер k онда iздестiру x сол ағаш астындада созылады. Егер k key[x], онда iздестiру оң ағаш астында созылады. Iздестiру жолының ұзындығы ағаштың биiктiгiн асып түспейдi, сондықтан iздестiрудiң уақыты (h - ағаштың биiктiгi) (h ) O бар.
Процедура iздестiру итератив нобайы
Procedure IterativeSearch (x, k);
begin
While (x ≠ nil) and (k ≠ key [x]) do
If k then x:= left[x] else x:= right[x];
Return (x)
end.
Минимум және максимум. Iздестiру ағашында ең төменгi кiлтпен элемент табуға болады, көрсеткіш left түбiрден өте шыға nil-ге жеткенімізге дейін табуға болады. (x ) Minimum(x) процедура түбiрi бар ағаш астынданың табылған элементiне көрсеткiштi қайтарады.
Procedure Minimum(x);
begin While left [x] ≠ nil do x:= left[x]; Return (x) end.
Алгоритм Maximum симметричен:
Procedure Maximum(x);
begin While (right [x] ≠ nil) do x:= right[x]; Return (x) end.
Екі алгоритм O(h) уақытты (ағаш бойымен тек қана төмен қозғалғандықтан) ағаштың биiктiгi талап етедi.
Келесi және алдыңғы элементтер. Егер х кейбір ағаштың көрсеткіші болса, сол Successor(x) рәсімі сілтегішті түйіншекке мен кейінгі x элемент немесе nil, егер көрсетілген элемент соңғы ағашқа қайтарады
Procedure Successor(x);
begin
If (right[x] ≠ nil) then Return Minimum (right[x]);
y:= p[x];
while(y ≠ nil) and (x=right [y]) do {x:= y; y:= parent[y]};
Return y
end.
Келтiрiлген процедура екi жағдайды бөлек қарастырылады. Егер шың x оң ағаш астындағысы бос болмаса, онда келесi x элементке - бұл ағаш астындада ең төменгi элемент және ([x ] right) Minimum тең бол. Болғанша, егер шың x оң ағаш астындасы бос болса, онда x жүр өз ата-анасын сол ұл болатын шыңды үстiне таппаймыз. Бұл (егер ол барып тұр) ата-ана және iзделiп отырған элемент болады. Процедура Successor ағашындағы жұмысын уақыты биiктiгінде(h ), өйткенi бiз тек - үстiне, немесе тек қана төмен қарай қозғаламыз. Predecessor процедура симметриялық.
Элементтiң қосымшасы.Процедура Insert (T, z) ағаш T қолайлы орынына элемент берiлгенге толықсытады.
Келтір- рәсім оқшау екі уақиғаны қарайды. x шыңының оң поддерево жым-жылас, сол кейінгі x элементті - ең төмен элемент осы поддереве және Minimum(right[x]) тең. x шыңының оң поддерево жым-жылас, сол вверх от x барамыз, әлі де шыңды таппаймыз, өзінің родителя сол ұлымен болып табыламын. Осы родитель(ол болса) және искомым элементпен болады. Successor рәсімінің жұмысының уақыты биіктіктің h ағашында болады Ο (h), себебі біз либо ғана вверх, либо ғана төмен жүреміз. Predecessor рәсімі симметрична.
Элементтің қосымшасы. Insert(T, z) рәсімі тапсырынды элементті T ағашының лайық жеріне үстейді.
Procedure Insert(T, z);
begin
y := nil; x := root;
while(x ≠ nil) do {y := x; if key[z] then x := left[x] else
x := right[x]};
p [z] := y;
ify = nil then root := z else if key[z] then left[y] := z else
right [y]:= z
end.
қосымша уақытты Ο (h) биіктіктің h ағашы үшін сұрайды.
Элементті өшіру. Өшіру рәсімінің өлшемі өшірілетін биіктіктегі z көрсеткіші болып табылады.Өшірудің үш жолы бар.Егер z-тің баласы жоқ болса,онда ата-анасының сәйкес полясына nil-ді қоя салу жеткілікті.Егер z-та бір бала болса, ата-анасымен бірге қалдырып, z-ті алып тастауға болады.Ал егер де баласы екеу болса, z-тің артындағы өз баласы жоқ келесі y элементін тауып аламыз.Енді кілт пен қосымша деректерді z биіктігінен y биіктігінекөшіруге болады, ал y биіктігін жоғарыда көрсетілген әдіспен өшіруге болады.
Қызыл-қара ағаштар
h биіктіктегі екі жақтыіздестіру ағашының негізгі операциясын O (h) іс-әрекеттері арқылы жүзеге асыруға болады.Егер ағаштардың биіктігі кішкене болса, нәтижелі болады. Операция нәтижесін арттыру үшін ағаштың биіктігі Ο (log n) өлшемінде керек болса,
ағаштарды салудың тиімді әдістері қолданылады. Бұндай әдістер ағаштарды тепе-теңдікте ұстау деп аталады. Тепе-теңдік сапасының әр түрлі өлшемдері қолданылады.
Ο (log n) өлшемдегі биіктікке қол жету үшін кепіл баға беретін іздеу ағаштарының теңестірілген бір түрі қызыл-қара ағаштар деп аталады.
Осындай теңестіру кезінде жиі кездесетіні АВЛ- теңестіру, онда әр бөліктегі сол жақ ағаш түбінің биіктігі оң жағынан бірлікке ғана ерекшеленеді.
Қызыл-қара ағаштар- іздеудің кеңейтілген екі жақты ағашы,биіктігі қара және қызыл болып бөлінеді:
Әр бөлігі не қара , не қызыл.
Әр парағы (nil-бөлігі)-қара.
Егер бөлігі қызыл болса, онда екі баласы қара.
1. Бас-басы түйіншек либо қызыл, либо қара.
2. Бас-басы парақ(nil- түйіншек) - қара.
3. Түйіншек қызыл, сол оба оның баласының қара.
4. Төмен түптен жапырақтарға, баратын барлық жолдар қара түйіншектің бірдей санын асырайды.
Түбірінен жапырақтарына дейінгі жолдар бірыңғай мөлшерде қара бөліктерді құрайды. 1-4 дейінгі қасиеттер RB-қасиеттері деп аталады. Қызыл-қара ағашының бөліктерін былай белгілейміз:
Node = (color, key, left, right, parent).
Айналу – бұл RB-қасиеттері бүлінген жағдайда қызыл-қара ағаштарды қалпына келтіру үшін жасалатын әрекеттер.Оларды Insert және Delete операцияларын жүзеге асыруда орындаймыз.Айналу кезінде бірнеше көрсеткіш ауысуы мүмкін, бірақ тәртібі сақталатын жүйелі операция болып табылады.
1-суретте біржақты екі айналу түрі көрсетілген:сол жаққа және оң жаққа
Жайылып өсетін ағаштар үшін бір операцияға есептегенде есептік құны O (log n)-ді құрайды.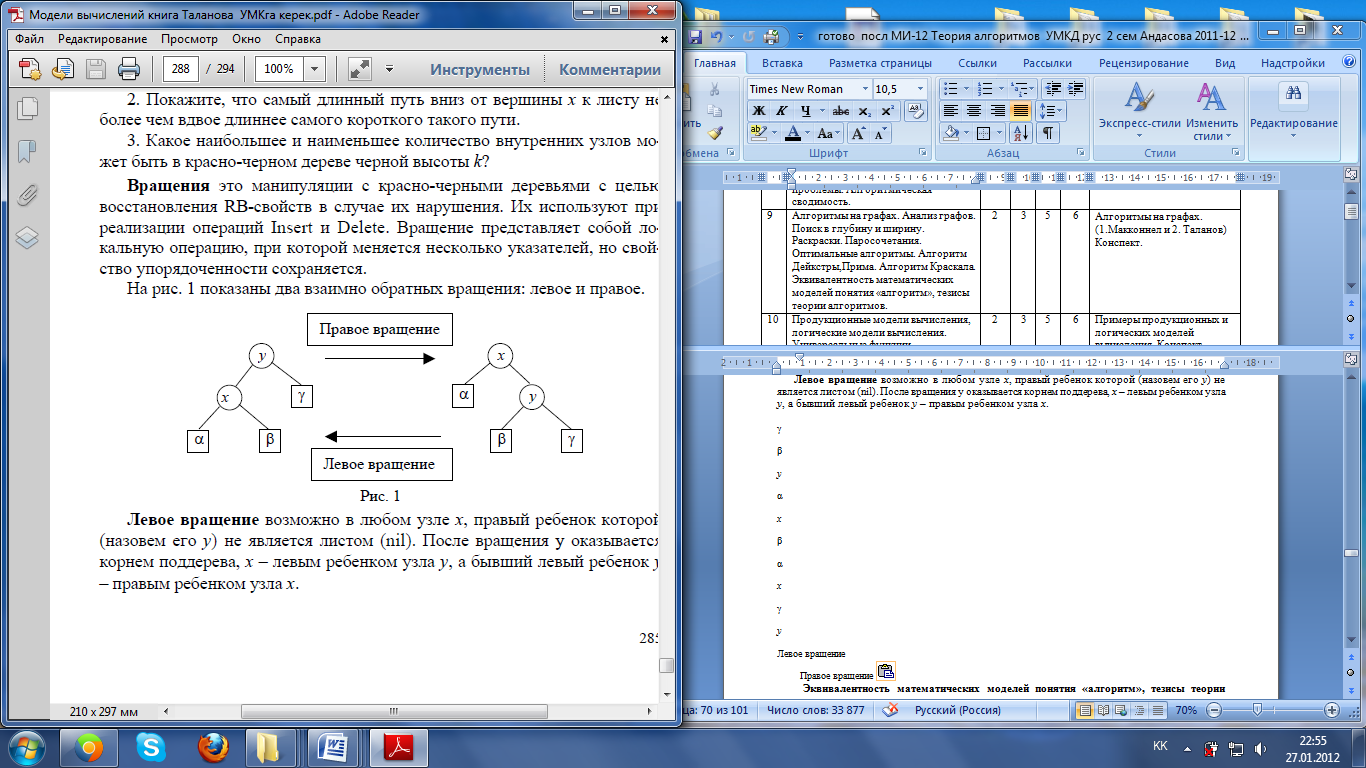
Б-ағаштары дегеніміз- магниттік дискіде немесе тікелей жеткізілетін құралдарда ақпаратты сақтауды қамтамасыз ететін теңестірілген ағаштардың бір түрі. Б-ағаштары қызыл–қара ағаштарға ұқсайды.Айырмашылығы мынада: қолданылатын дисктің мінездемесіне қарай Б-ағаштарының бөліктерінде көп бала, іс жүзінде мыңға дейін болуы мүмкін.Осыған байланысты ағаштың биіктігі O (log n)-ді бағалау нәтижесі бойынша қызыл–қара ағаштарға қарағанда айтарлықтай аз мөлшерде. Қызыл–қара ағаштар сияқты Б-ағаштары да O (log n) мерзімінде көптеген n өлшемдегі әр қилы операцияларды жүзеге асыра алады.
x түйіншегі, сақта- n[x] кілттердің, n имеет[x] + 1 бала-шағалардың. x кілттерге деген сақтал- қызмет ет- барлық оның бұтақтарын бас n бөлетін шекаралармен[x] + 1 топтардың; үшін бас-басы топты бір x бала-шағаларынан жауап береді. При ізденісте Б-дереве біз искомый кілтті мен n салыстырамыз[x] ара x сақталатын кілттермен, қарамастан және дейін ре-зультатам салыстыр- сайлаймыз
Дискте берілген деректер құрылымдағы жұмыстардың ерекшеліктері.
Б-ағаштарымен қызмет атқаратын алгаритмдердің оперативті есте сақтау қабілеті барлық ақпараттың аз мөлшерін ғана (бөліктердің белгілі санын) қамтиды.
Диск естің үлкен аумағы болып табылады, келесі х нысанымен жұмыс істеу үшін біз Disk-Read(x) арнайы(дискке жазу)операциясын орындауымыз керек.
Бағдарламаның жұмыс уақыты негізінен осы операциялардың санымен анықталады, сондықтан да Б-ағашының бөлігі дисктің бір бөлшегін түгелдей толтыру үшін бар ақпаратты бірден оқып, жазып отыру керек.Осылайша, тармақтану дәрежесі(бөліктегі бала саны) өлшемімен анықталады.
Б-ағашының типтік тармақтану дәрежесі элементтің өлшеміне байланысты 50 мен 2000 арасында болады. Іздеу барысында тармақтану дәрежесінің артуы ағаш биіктігі мен дискке оралу санын тез арада қысқартады. Мысалы,биіктігі 2 және 1001 дәрежедегі Б- ағашы миллиардтан астам кілтті сақтауы мүмкін. Тамырды үнемі оперативті есте сақтауға болатынын ескерсек, керекті кілтті іздегенде, дискке екі рет оралу жеткілікті.
Ескерту. Б-ағаштарының басқа жиі пайдаланылады ақпарат көп орыны бар жапырақтарда орналасады, себебі кілтті сақтамауға да болады, ал ішкі бөліктерде тек қана кілттер мен балаларға көрсеткіштер сақталады.
Б-ағаштарымен жүргізілетін негізгі операциялар. Б-ағашының тамыры әрқашанда оперативті есте болады деп санауға болады,өйткені дисктен оқу операциясы тамыр үшін қажет етілмейді; дегенмен де біз ылғи да тамырды өзгерткенде, дискте сақтауымыз керек.
Б-ағашында іздеу.Б-ағашында іздеу қос ағашта іздеуге ұқсас. Айырмашылығы мынада: біз х-тің әр бөлігінде (n[x] + 1)-тің екеуін емес, бір вариантын таңдаймыз.Іздеу барысында ағаштың тамырдан жапырақтарына дейінгі бөліктері қаралады.Сондықтан да дискке оралу көрсеткіші θ(h) = θ(logt n) тең, мұндағы h – ағаштың биіктігі, ал n – кілттер саны. n[x] ≤ 2t болғанда, онда while циклы O(t) рет, және де санау уақыты O(th) = O(t⋅logt n)-ға тең.
және оны орналастыратын іс-шара арқылы жасалады.Оны O(1) уақыт ішінде дисктен оқу операциясын қолданбай-ақ жүзеге асыруға болады.
Y бөлігінде қалыптасқанша 2t бала болды ; қалыптасқаннан кейін t ең кішісі қалды, ал қалғандары t жаңа z бөлігінің балалары болады, олар өз кезегінде х бөлігінің баласы болады. y бөлігінің медиана-кілті x бөлігіне қосылады даy бөлігі мен оның артындағы z бөлігін айырып тұрады.
Элементке қосылған Б-ағашы. Бұл операция қолданудан алдын процедурада қолданылады.Барлығының сынуынан бөліп екі бөлікке бөлінеді.Атқарушы t-1 элементі әрқайсысында болады.
Алдын бұл кілт-медианасы key [y] жіберіледі. Ол х бөлігі у қойылады. Бұл мән орындалған жағдайда х толық болмайды. Алайда у-түбір процедурасы анологиялық жүмыс атқарады. Бұл жағдайда ағаш ұлғайады.
Insert процедура Б-ағашқа к элемент қосады. Түбірден жапыраққа дейін бір рет өтеді. O(th) = O(t·logt n) уақыт керек және O(h) дискіге қарасты. Ағаштың биіктігі һ болса жұмыстың барысы бойынша ұсақтау процедурасы бойынша кездесетін толық бөлінеді. Толық бетпен ауыстыратын, яғни толық емес бетке жақын болады.Ал оны бөлуге болады. Ол оған жақын қосымшалар. Кілті сол үшін жоғары көтеріледі және оны толық емес элементтерге қосамыз.
Б-ағашын өшірілуі. Б-ағашының элементтен өшірілуі ол аналитикалыққа кіреді,қиын болмаса да. Оқырмандарға көрсетілетін процедураларда мүмкін өшіріледі. Бөлікте құралған О һ жүктеледі. Б-ағаштан ұзын һ, сосын оған барлық процедуралар жүктеледі O(t·h) = O(t·logt n).
Қорытындыда байқайтынымыз аға балансталған және Б-ағашы кітаптан қарастыру болады. Кнута Ахо, Хопкрофта және Ульмана және Седжвика. Тура баламадан Б-ағашын кітаптан Кормена және басқалар Тибас және Сиджвик қарастырады және олардың әр түрлі болатынын айтты. Ағаштың құрамында қосылатын қызыл-қара және 2-3-4 ағаштар.
1970 жылы Хопкрофт бұл тұжырымдамаларды 2-3 ағаштарды және алдында айтылған Б-ағашын және 2-3-4 ағаштарды қарастырды. Бұл ағаштардың әрқайсысы бұтақтарды немесе үш бұтақтан бола алады. Б-ағашын арнайы Байером және Мак Крейтом 1972 жылы қарастырды.
Кеңістікті іздеу.
Жоғары алгоритмнің жұмысы, жоғары нүктелері мен қабырғаларын қарастырады. Қандайда бір жағдайда орындалатын нүктелерді алдыннан қарастырады. Қарастырылмаған шыңда жана деп алайық. Соған қатысты қарастырылған шың ашық болып қала береді.Сосын ғана жабық болады.
Қабырғаны кеңдігіне қарай қарау идеясының мәні алдын ала тандалған немесе берілген басты а шыңының кезекпен өшірілгендерді қарастыра алуында. Басқаша айтқанда, ең алдымен а шыңның өзі қарастырылады, сосын барлыщ шыңдар, а-мен қосылған,яғни 1 қашықтығының арасында орналасқан,ал содан кейін 2 қашықтығының арасында орналасқандар және т.б.
а бастамалық шыңға іздеу алгоритмын қарастырайық. Ең бірінші а шыңы қарастырылады, ол жалғыз ашық шыңға айналады. Бұл шың активті болады. Әрі қарай әрбір қадам х ашық шыңынан басталады. Ары қарай активті шыңға қатысты қабырғалар зерттеледі. Егер бұндай қабырға жаңа х шыңы у-ке қосылса, онда у шыңы қарастырылады да, ашық шыңға айналады. Активті шыңға қатысты зертелгеннен кейін, ол активті болмай, жабыққа айналады. Содан кейін жаңа активті шың тандалады, және жұмыс барысы қайталанады.Көптеген ашық шыңдар бос болғанда, процессс аяқталады.
Кеңістікте іздеудің басты ерекшелігі, ол графқа көшу амалы басқашалығында, Алдындағы ашық шыңдардың бірінен тандалынады. Стартқа шың жақын болса, ол тез қарастырылады.
(BFS –ағылшын тіліндегі алгоритмнің мағынасы – Breadth First Search) біт старттық а шыңынан кеңістіктегі іздеу шыңындағы процедурасын қарастырайық. Көптеген барлық шың қарастырылады. Х шыңына жақын, Q-ашық шыңның кезегі.
Procedure BFS(a)
1 a шыңын қарастыру
2 a ⇒Q
3 while Q ≠ ∅do
4 x ⇐Q
5 for y ∈V(x) do
6 исследовать ребро (x, y)
7 if вершина y новая
8 theny шыңын қарастыру
9 y ⇐Q
Тереңдігіне қарай іздеу методы.
Тереңдігіне іздеу-графты көшіру стратегиясындағы көптік орнатылғандардан ең маңыздысы юолып табылады . Бұл қадам жаңа ойларды орындай алатындай және де жанындағылар зерттелгенде, бір қадам артқа тастайды. Тереңдәкке іздеу методы кхптеген аттармен анықталған, мысалы «бэктрекинг», «қайтаруымен іздеу».
Жаңа ұғымдар, ашық және белсенді шыңдардың ізденісі үшін осындай тереңждік мағынасына ие. Және де сол сияқты ізденісте енеді. Бұл бір белсенді шыңының ылғи астамын ар екенін белгілейміз.
Айналып кетуінің орындалуы бастапқы шыңының қатысуымен дегеннен басталады, белсенді қайсыбір және бірден-бір ашық шыңмен болады. Кейін қақтығыс шыңға А қабырға және у шыңы қатысуымен таңдалады. Ол ашық және белсенді болады. Ізденісте енді А шыңы белсенді қалғаны осы кездерден бйқаймыз. Оған барлық қақтығыстың қабырғаларын әлі де зерттеуге болмайды. Ендігі осы сияқты және алдыңғы ізденісте ірбңр кезекті адым ашық шыңның көпшілігінен таңдау бір ғана емес зерттеу қабырғалардан, (х,у) әйтпесе сол қабырға зерттеледі. У жаңа шыңы, ол ашыққа дегенінің қатысуымен айгалады.( уа.
Басты өзгелік ендігі ізденістен, алдыңғы ізденіске тереңдігінің аралық сапасы белсенді, сол ашық шыңдардан ғана құрылады. Нешінші рет шыңның қатысуы соңғы болады. Ол үшін талғамның мынадай ережесінің жүзеге асуы ашық шыңының көпшілігіне сақтап, құрылымымен жіңішесі болфп табылады. Аш-шыңдар ғана осы тәртіпте жіңішке болып бүктеледі, олар арадағы қандай да бір ашылыстың, ал аралық сапа белсенді соңғы шың шық. Сол жүйілік 2.2 суретте көрсетілген.
Жіңішке үшін ашық шыңдарды Sарқылы белгілейміз, қалған белгілер баяғы мағынаны сақтайды, және де алғашқы тараудағы top(s) арқылы мағынасы аз ғана болады. Соңғы қосылған элемент сыртының элементі. Байлныстың бір компоненті айналып кетуінің рәсімі ізденістер әдісінің тереңдікке А шыңымен бағаланады. Мүмкін сонда келесі бейнемен жазуға болады.
Procedure DFS(a)
1 А шыңына тоқталу
2 a⇒S
3 while S ≠ ∅do
4 x = top(S)
5 if емес зерттеу қабырғасы (x, y) бар
6 then зерттеу қабырғасы (x, y)
7 if у жаңа шың
8 then у шыңына тоқталу
9 Sy⇒
10 elseх-ті s –тен алыстату
Тағы бір рет көңіл аударсақ осы рәсімінің негізгі өзгелігіне ізденістер тәрізді рәсімін енді көзге іле аламыз. Алдыңғы ізденісте шың белсенді қойылып, сонымен қалады, әлі-де толық зерттелмегендіктен оның маңайы болмайды., одан кейін ол берік болады.
Алдыңғы ізденісте тереңдігінің, х белсенді шыңының маңайында у жаңа шыңы кездессе, сол стекке салады. Және алдыңғы while топтамасының келесі қайталаушылығында белсенді болады. Бұл ретте х стекте қалады және әлдеқайдағы уақыт аралығында тағы белсенді бола түседі. Әтпесе айтарлық, өақтығыстар х шыңының қабырғалары үздік-үздік зерттеуі қатар болады.
Алгоритмнің барлық бағандарының айналып кетуі, сол жағдайдағы кеңейуінің арасындағы ізденіс. (1-алгоритм). Тек қана стекті ауыстыруы керек. Ал рәсімі BFS-рәсімі DFS.

1-ші және 2-ші сипаттау ізденісі алғашқы тарауды белгіленуі сақталдаы. Және де ізденісі үшін тереңдетіледі. O(m+n) дұрыс арапшылығы қалады, бірақ онығң айғағы бірнеше өзге пайымдарын сұрайды . себебі, енді сол сияқты бірнеше шың реттің белсенді болуы мүмкін. Алайда бас-басы қабырғаға ғана екі рет қарастырылады, сол себептен IF операторы 5 ші жолда then (6-9 жолдар) реттің тармағы . O(m) қайталанылады. Осы оператордың else (10 жол) реттің тармағы O(n) қайталанылады, сол сияқты әрбір бастапқы шыңы стектен бір рет алыстатылуы мүмкін. Арадағы бүтіндікте O(m+n) алынады. Алғашқы тарауда ескертпелер туралы сол жерді сарапшалаған әділдік жасағандар қалады, алдындағы жер нешінші рет сол бағаны қамтиды.
Шыңның өрнегі
Шыңның өрнегінің бағаны деп-түстің мақсатындағы оның шыңдарын айтады. Кәдімгі түстер –ол 1,2...,к сандары. Онда өрнек функция болып табылады, белгілі бір көпшілікте шыңның ббағаны және қабылдаушы тағайынды көпшілікті шың сияқты{1,2,...,3}. Шыңды тағы бөлу көпшілік шыңы ретінде қарастыруға болды. V = V1 ∪V2 ∪ … ∪Vk, Vi – і түсінің көпшілігі үшін. Vi –көпшілкгі түсті сыныптармен атайды. Өрнек дұрыс деп аталады-егерде әрбір түс көпшілікті сыныптармен тәуелсіз болса, айтпесе дұрыс шыңның әрбір екі шектес шыңы әртүрлі түстерді қажет етеді. Тапсырыс туралы өрнекте түстің аздаған санына айталмыш бағаны G дұрыс өрнегін табу құрылады. Сол сан хроматикалық сан бағаны деп аталады және көрсетіледі x(G)
Дұрыс шыңның толық бағаны knбарлық өрнегі бөлек –бөлек түстерді керек етеді. Сол себептен χ(Kn) = n. Егерде қайсы-бірі бағанда толық подграф шыңдарымен, сол осы шыңның мына подграфы к түстерін қажет етеді. Осыған тиіс кез келген бағаны үшін емесабатшылық орындалады. χ(G) ≥ ω(G). (3.1)
Алайда хроматиклық сан үлкен қатал сан болуы мүмкін. Айталық: ұзындықтың топтамасы үшін 5 ω(C5) = 2, ал χ(C5) = 3. Басқа мысалдар 3.3 сіретте көрсетілген.
Онда бағаны нешінші болған шыңдары 4-түсте (шыңның түстері жақшада көрсетілген) бейнеленген. Оны тексеру қиын емес, үш түс осы дұрыс боялған оның бағаны жеткіліксіз. 4-мысалда осы бағанның емесабытшылығы орындалады.
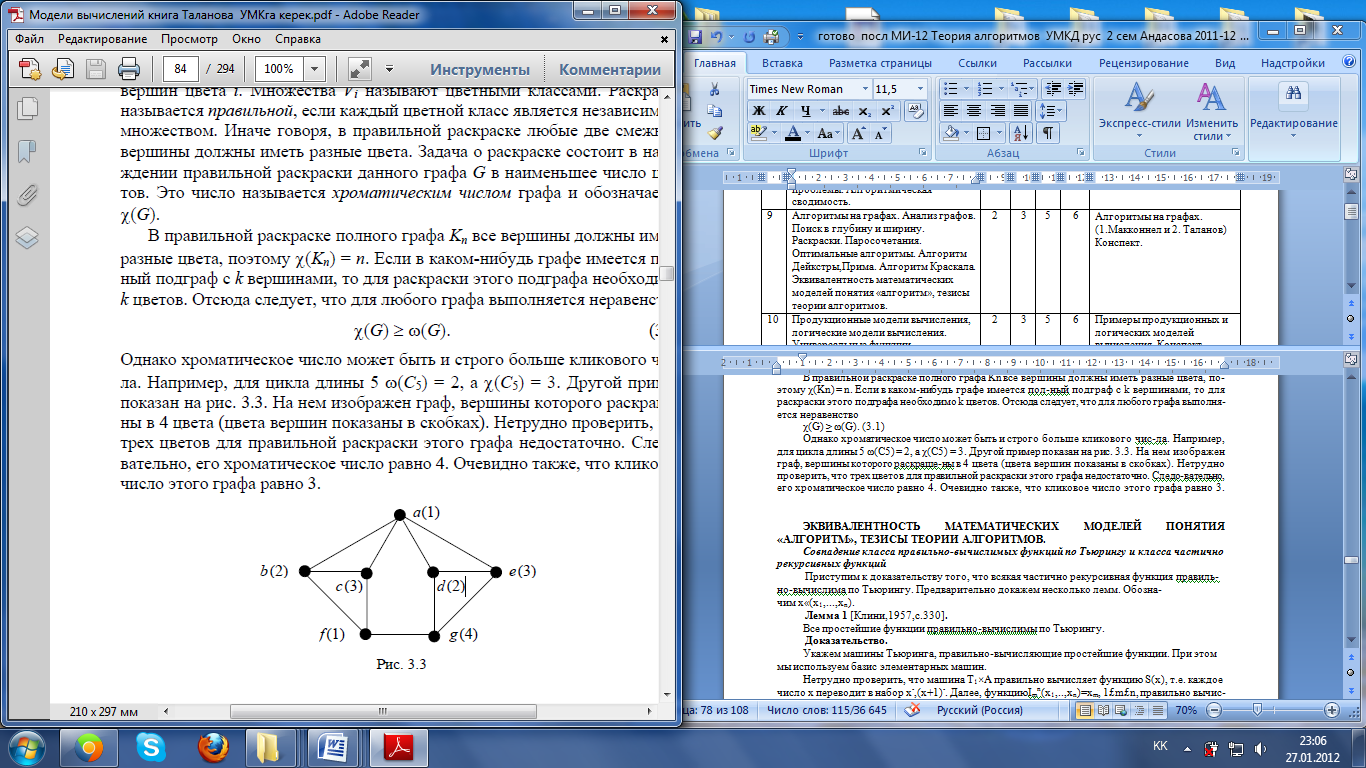
Қабырғаның өрнегі
Түзумен берілген тапсырма туралы шыңның өрнегінің тапсырмасы туралы бағананың қабырғасының өрнегінде бар түстер қабырғаларына қашан тағайындалады. Қабырғаның өрнегі –көрінген ортақ шың, берілген екі қабырғада аламаштаса дұрыс болады. Боялған әртүрлі түстермен. Түстің бағаны G қабырғасының дұрыс өрнегі үшін қжетті, ең төмен саны бағанның хроматикалық әріпсанымен аталады және
X’(G) арқылы көрсетіледі. Δ(G) арқылы шыңның χ′(G). Ең көп дәрежесін белгілейміз.
Сәйкестік және қабырғаның жабындылары. Үмітсіз ортақ шыңдар сәйкестік болғанда қабырғаның көпшілігі қос-қостан аталады. Сәйкестік бағандар көпшілікті өрнегі деп-қабырғаның ортақ шыңы болмау н айтамыз. Тапсырма сәйкестік жайлы ол берілген бағанда сәйкестік үлкен санның өрнегімен құрылады. Ол сан баған үшін G деп алып оны π(G). айтамыз. Өрнекті жабық бағанмен мынадай көпшілікте аталады, егерде оның әрбір өрнегінің ұштарының бағасы қақтығыс болуы бірде бір өрнекпен болуы мүмкін. Қабырғасының аздаған саны қабырғада жабық бағанды G арқылы ρ(G) белгілейміз. Қабырғаның жабындысының шыңдармен оңаша өмір сүруі ғана қалғанын байқаймыз.
Сәйкестік ұйғарымы сияқты шыңның тәуелсіз көпшілігінің ұйғарымын, сәйкестік анда санда қабырғанңы тәуелсіз көпшілігін айтамыз. Сол аналогия тағы тығыз байланыстың өрнегінің жабындыларының арасында қатайады. Сол сияқты шыңның өздерінің арасындағы жабынды тәуелсіз және тоқулы көпшіліктер келісімі. Тіпті бірдей сан білдірсе осы байланысты, ашып-жарып мынадай көріністі ескертеміз, G тәуелсіздігінің а (сандары).
В-ағаштар
Сыртқы жадыдағы деректерді іздеу үшін негізгі «ағаш тәріздес» аппараты В-ағаштар болады. Осы механизмдер негізінде келесі ойлар бар. Біріншіден, жалпы қолжетімдік уақыты дәйекті түрде орналасқан мәліметтер көлемімен емес, магниттік шаласының келу уақытымен анықталатын сыртқы жадыдағы деректер құрылымы жайлы сөз қозғағаннан кейін, бір рет сыртқы жадыға сұрау салған соң бірнеше мәлімет алған тиімді, сонымен қатар бұл жерде негізгі жадының үнемді қолданылуын ескеру қажет. Негізгі жадыны ұйымдастыруды бірдей көлемді парақтар жинағы түрінде қарастыратын болсақ, онда осы парақты сыртқы жадымен мәлімет алмасу бірлігі деп қарастырған жөн. Екіншіден, сыртқы жадыдағы іздеу құрылымын құрастырудың тиімді түрін қолану барысында кез келген кілт бойынша ақпаратты іздеу саны алдын ала мәлім сыртқы жадымен ақпарат алмасуды қажет етуі тиіс.
Классикалық B-ағаштар
Классикалық B-ағаштар механизмі 1970 жылы Бэйер және Маккрейтпен ұсынылған. N ретінің B-ағашы сыртқы жадының сатылы байланысқан беттері (ағаштың әрбір басы – бет) түрінде бейнеленіледі, олар келесі қасиеттерге ие:
Әрбір бет 2*n элементтерінен көп емес (кілтпен бірге жазбалар).
Әрбір бет түбірліктен өзге, n-нен кем емес элементтен құралады.
Егер В-ағаштың ішкі (беттік емес) басы m кілттерінен құралса, онда m+1 бет-тұқымдары бар.
Барлық парақтық беттер бір деңгейде орналасқан.
B+-ағаштар
Классикалық В-ағаштар ұйымдастырылу сызбасы қарапайым, дегенмен практикалық қолданыс үшін тиімді емес. Оның ең басты себебі практикалық қолданыста көбіне сыртқы жадыда тек қана кілттерді емес, сонымен қатар жазбаларды сақтау қажет. В-ағашында элементтер ішкі де, сыртқы да парақтық беттерінде орналасады, ал жазба көлемі үлкен болуы мүмкін. Ішкі беттері көп элементтерден құрала алмайды, оның себебі ағаш терең болуы мүмкіндігінде. Осыған орай, ағаштың төменгі деңгейлерінде кілттер мен жазбаларға қолжету үшін сыртқы жадымен көп мәлімет алмасу қажет.
Деректер қорындағы индекстерді ұйымдастыру үшін B+-ағаштар түрлері
B+-ағаштар деректер қорларындағы индекстерді ұйымдастыру үшін қарқынды түрде қолданылады. Ең алдымен, аталмыш ағаштар екі қасиеттерімен айқындалады: кез келген кілт пен тақырыпты іздеу үшін сыртқы жадымен мәлімет алмасу санының алдын ала болжанылуы мен ағаш бұтақтарының көп болуына байланысты осы мәлімет алмасу санының ең үлкен кестелерді индекстеу кезінде де көп болмауы.
R-ағаштар және олардың кеңістік деректер қорындағы индекстерді ұйымдастыру үшін қолдану
Кеңістік деректер қоры индексін ұйымдастыру үшін қолданылатын В-ағаштары механизмінің тағы бір ұлғайған түрі – R-ағаштары. В-ағаштары сияқты олар бұтақ тәріздес болып келеді, алайда R-ағаштарындағы мәлімет В-ағаштарындағы мәліметтерден айырмашылығы бар. Парақтық беттерде орналасқан кеңістік объектілердің идентификаторларынан өзге R-ағаштарында индекстелетін объектінің шекаралары туралы ақпарат сақталады.
Сыртқы жадыдағы іздеу үшін хештеу әдістері .Хэштеу негізіндегі (қажет мәліметтерді бір рет сұраудан соң алу мүмкіндігі) сыртқы жадыдағы мәліметтерге қол жеткізу идеясы тиімділігі сонша, одан бас тарту қиын. Сыртқы жадыдағы мәліметтерді хеширлеудің авторы Витольд Литвин болып табылады. Бастапқы идея айқын көрінеді: егер хэштеу негізінде мәліметтерді басқару кезінде негізгі жадыда хэш-функция қажетті элементтің адресін өндірсе, онда сыртқы жадыға сұрау салғанда дисктік кеңістіктің блогының нөмірін генерациялау қажет. Басты кедергілер коллизияларға қатысты.
Кеңейетін хэштеу .Кеңейетін хэштеу (Extendible Hashing) негізінде негізгі жадыдағы сандық іздеу ағаштарын қолдануда жатыр. Негізгі жадыда сандық іздеудің бинарлық ағаштары негізінде жасалған анықтама бар, олардың кілттері хэш-функциялар мәні. Осы жағдайда, сандық іздеу ағашындағы іздеу «сәтті» жүргізіледі, басқаша айтқанда сыртқы жадының кейбір блогына алып келеді.
Сызықтық хэштеу. Сызықтық хэштеу идеясы (Витольд Литвин) негізгі жадыда анықтаманы орналастырмауда болып отыр. Әдістің бастысы сыртқы жады блогына жіберу үшін әрқашан хэш-функцияның кіші мәні биттерін қолдану. Егер бөлшектеу қажеттілігі туындаса, онда жіберу дұрыс қалатындай етіліп, блок бойынша қайта үлестіріледі.
Деректер қорындағы индекстерді ұйымдастыру үшін хэштеуді қолдану
Деректер қорында хэштеу әдісі бүгінгі күні сирек қолданылады. Хэштеу әдісін бастапқы кезден қолданып келе жатқан жүйелердің ерекше түрі ретінде Ingres-ті айта аламыз. Оның себебі анық. Хэштеу пайда болған күннен ерекше кілт бойынша іздеуге бағдарланған еді. Ең кең таралған әдістер толыққанды қамтамасыз ете алмайды. Дегенмен, бірте-бірте хэштеу технологиясы және В-ағаштар технологиясымен бірігіп, әлемдегі ең негізгі деректер қорына айналуы мүмкін.
Деректер қорындағы іздеудің жанама әдістері: Байланыс индекстері және биттік шкаланы қолдану негізіндегі индекстер.
Қолданылған әдебиеттердің тізімі: [1]-[23]
Лекция № 3. Есептеулер модельдері. Тьюринг машиналары.
Чёрч- Тьюринг тезисі
Есептеулер модельдерінің үш түрі бар:
1) Тьюринг машинасы
2) Лямбда есептеу (рекурсия)
3) Комбинаторлық логика
Тьюринг машинасы – бұл абстрактты орындаушы (абстрактты есептеу машинасы), 1936 жылы алгоритм ұғымын формальдау үшін Алан Тьюринг ұсынды. абстрактты орындаушы (абстрактты есептеу машинасы). Тьюринг машинасы – ақырлы автоматтың кеңейтілген түрі, басқа орындаушыларды қадамдап есептеу процесін жүзеге асырып имитациялай алады (өту ережелерін беру арқылы қарапайым), қадамдар аса қарапайым.
Тьюринг машинасының құрамы:
1 ) екі жағы шексіз лентадан (олар ұяшыққа бөлінген)
2) басқару құралы,осы күйлердің біреуінде болады
3) күйлер жиыны. Күйлердің саны шектеулі және нақты беріледі
Басқару құралы лентада солға, оңға жылжи алады, лентаға қандай да бір ақырлы алфавиттің символдарын жазады не оқиды. Бос символ болады, ол лентаның кірістік деректер жазылмаған,қалған ұяшықтарына жазылады.
Басқару құралы өту ережесі бойынша жұмыс істейді. Өту ережесі Тьюринг машинасында жүзеге асатын алгоритм. Өтудің әрбір ережесі Тьюринг машинасына ағымдағы күймен ағымдағы ұяшықтағы символға байланысты, осы клеткаға жаңа символ жазуды, жаңа күйге өтуге немесе бір клеткаға оңға немесе солға жылжуға бұйрық береді.
Тьюринг машинасының кейбір күйлері терминалды деп белгіленеді, бұл күйге өту жұмыстың аяқталмағанын, яғни алгоритмнің тоқтағанын білдіреді. Бір ғана ережеден тұратын Тьюринг машинасы анықталған (детерминирленген) Тьюринг машинасы деп аталады, ал егер екі немесе одан да көп командасы болатын «лента символы — күй» жұбы бар болса, мұндай Тьюринг машинасы анықталмаған (детерминирленбеген) деп аталады.
Тьюринг машинасын анықтау үшін мыналар көрсетіледі:
Сыртқы алфавит
A= {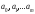 }
} 
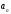 - ұяшықтың бос символы
- ұяшықтың бос символы
Ішкі күйлердің алфавиті немесе оны ішкі алфавит деп атаймыз.
Q = { 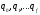 } , мұндағы
} , мұндағы 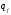 - тоқтаудың күйі. Осыған келгенде машина жұмысын тоқтатады.
- тоқтаудың күйі. Осыған келгенде машина жұмысын тоқтатады. 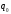 - бастапқы күй, машина жұмысын бастайды.
- бастапқы күй, машина жұмысын бастайды.
Программа (функционалды схема), ол – команда деп аталатын өрнектердің жиынтығы. Мынандай әрбір жұп үшін (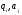 )
) 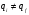 тек бір ғана команда болады.
тек бір ғана команда болады.
Ереженің жалпы түрі:
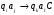
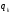 - жаңа күй, ол кейде
- жаңа күй, ол кейде 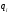 қалуы мүмкін.
қалуы мүмкін.
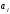 -
- 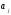 -ның орнына жазылатын жаңа символ
-ның орнына жазылатын жаңа символ
Тьюринг машинасын сипаттау үшін бастапқы және соңғы күйді (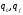 ), лентадағы бастапқы орналасуды және басқару құрылғысының бас тиегінің орнын көрсету керек.
), лентадағы бастапқы орналасуды және басқару құрылғысының бас тиегінің орнын көрсету керек.
Тьюринг бойынша толықтық. Тьюринг машинасында басқа машиналарды (Пост машинасын, Марковтың нормальды алгоритмдерін) және кірістік деректерді қандай да бір алгоритм арқылы шығыстық деректерге түрлендіретін компьютердің программаларын имитациялауға болады. Ол сызықты жады бар қарапайым есептеу машинасы, формальды ережелер бойынша кірістік деректерді элементар (яғни әр әрекет тек жадтың бір ұяшығын ғана өзгертеді және әрекеттер саны ақырлы) әрекеттер тізбегі арқылы түрлендіреді.
Тьюринг машинасы бір ұяшықтан тұратын жадысы бар машина болғандықтан, оның әрекеттері қарапайым және мүмкін әрекеттердің саны шектеулі. Тьюринг машинасы қарапайым болса да, онда басқа машинада есептелінетіндердің барлығын есептеуге болады. Бірақ ол есептеулер қарапайым әрекеттердің тізбегі болу керек. Осы қасиетті толықтық деп аталады.
Тьюринг машинасын имитациялай алатын абстрактты орындаушыларды Тьюринг бойынша толық деп атайды.
Унарлық санау жүйесінде сандарды көбейтуге арналған Тьюринг машинасының мысалы. Машина келесі ережелер бойынша жұмыс істейді:
| Ережелер | Ережелер |
| q0*→q0R | q4a→q4aR |
| q01→q0R | q4=→q4=R |
| q0×→q1×R | q41→q41R |
| q11→q2aR | q4*→q51R |
| q21→q21L | q5*→q2*L |
| q2a→q2aL | q6a→q61R |
| q2=→q2=L | q6×→q7×R |
| q2×→q3×L | q7a→q7aR |
| q31 → q4aR | q71→q2aR |
| q3a→q3aL | q7=→q8=L |
| q3*→q6*R | q8a→q81L |
| q4×→q4×R | q8×→q9H |
1930-жылдардың ортасында Алонзо Чёрч пен Алан Тьюринг айтқан бұл тұжырым —есептелу теориясы, информатика, теориялық кибернетика және т.б. ғылым салалары үшін іргелі тұжырым. Алан Тьюринг мынандай жорамал айтты (оны Чёрч — Тьюринг тезисі дейді):
«Кез келген алгоритм осы сөздің интуициялық мағынасында эквивалентті Тьюринг машинасымен көрсетіле алады».
Жалпы түрде бұл Чёрч-Тьюрингтің тезисі былай дейді: «Кез келген интуициялық есептелетін функция жартылай есептелетін функция, яғни қандай да бір Тьюринг машинасымен есептеліне алады».
Чёрч-Тьюрингтің физикалық тезисі:
«Физикалық құрылғымен есептеліне алатын кез келген функция Тьюринг машинасымен де есептеліне алады».
Тьюринг машинасы Пост машинасын Марковтың нормальды алгоритмдері және компьютердегі кез – келген программаны (кірістік деректерді қандай да бір алгоритм бойынша шығыстық деректерге түрлендіретін) имитация жасай алады. Өз кезегінде түрлі абстрактілі орындаушылар Тьюринг машинасын имитациялай алады. Мұндай орындаушыларды Тьюринг бойынша толық деп атайды. Тьюринг машинасын имитациялайтын программалар бар (компьютерлерге арналған), бірақ оның имитациясы толық емес, өйткені Тьюринг машинасының лентасы екі жағынан да шексіз, ал компьютер жады шектеулі.
Тьюринг машинасының моделі өзін кеңейтуге мүмкіндік береді. Ленталардың кез – келген саны бар және көпөлшемді ленталардан тұратын Тьюринг машиналарын қарастыруға болады. Олардың барлығы Тьюринг машинасы бойынша толық болады және кәдімгі Тьюринг машинасымен модельденеді.
Тьюринг машинасының түрлері:
Жартылай шексіз лентада жұмыс істейтін Тьюринг машинасы
2 өлшемді Тьюринг машинасы (Муравей Ленгтона);
Әмбебап Тьюринг машинасы;
Тьюрингтің анықталмаған (детерминирленбеген) машинасы;
Тьюрингтің ықтималдық машинасы;
Тьюрингтің селкілдегі (Тьюринговская трясина).
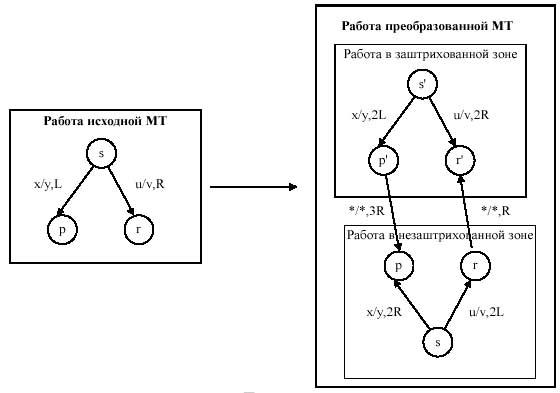
Жартылай шексіз лентада жұмыс істейтін Тьюринг машинасы. Мұндай машинаны Тьюринг машинасына өзгерту оңай, ол үшін ұяшықтарды қайта нөмірлейді, күйлердің санын 2 еселейді, басқару құрылғысының қозғалысын реттейді.

* белгісі Тьюринг машинасының сөздігінде сақталмайды, штрихталған зонада шекараға жеткендігін білдіреді, ал бастапқы күй жартылай шексіз лентада қай жерде тұрса, мұнда да сол жерде тұрады.
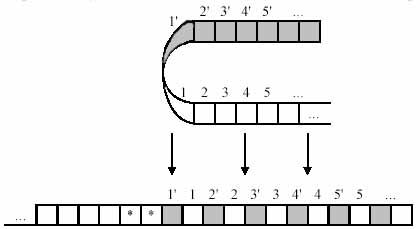
Машина штрихталмаған зонада жұмыс істейді. Еер жұмыс кезінде ‘*’ символы кезіксе, оқу-жазу бастиегі зона шекарасына жеткені. Лентаның «*» сол жағындағылар бұл машинада қарастырылмайды. Жаңа Тьюринг машинасының бастапқы күйі бастапқы машинадағыдай жақта орналасады.
Төменде жартылай шексіз лентада жұмыс істейтін Тьюринг машинасы жұмысының схемасы берілген:
Тьюрингтің ықтималдық машинасында лентадағы күйден және лентаның мәндерінен бірнеше күйге өтудің мүмкіндігі болады. Бұл машина өтудің нұсқасын қандай да бір ықтималдықпен таңдайды (монета лақтыру) және анықталмаған (недетерминированная) Тьюринг машинасына ұқсас.
Тьюрингтің ықтималдық машинасында полиномды уақыт ішінде жұмысын аяқтап 1/3 аз қатемен жауап қайтаратын алгоритмдер класын BPP класы деп атайды.
Есептелу теориясында орындаушы тьюринг-толық деп аталады, егер онда кез келген есептелетін функцияны жүзеге асыруға келсе.
Мысалы программалау тілдерінің көпшілігі (Паскаль императивті тілі, , Haskell функциональды тілі, Prolog логикалық тілі) және грамматиканың жалпы түрі де тьюринг-толық. Ал ақырлы автоматтар, жай рекурсивті функциялар, контксті-бос грамматика, регулырлы грамматика тьюринг толық емес.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Виртуальная реальность (1.11 MB)
Виртуальная реальность (1.11 MB)
 0
0 606
606 3
3 Нравится
0
Нравится
0



