Вероятностные задачи в ГИА 9,11 классах

Теория вероятностей и комбинаторные правила решения задач

МОУ № 12 г. о.Жуковский

Богданова С.В.

Эпиграф урока:

«Число, место и комбинация – три взаимно перекрещивающиеся, но отличные сферы мышления, к которым можно отнести все математические идеи».

Дж. Сильвестр

.

.

Классическое определение вероятности

Стохастическим называют опыт, если заранее нельзя предугадать его результаты. Результаты (исходы) такого опыта называются событиями .

Пример: выбрасывается игральный кубик (опыт);

выпадает двойка (событие).

Событие, которое обязательно произойдет в результате испытания, называется достоверным , а которое не может произойти, - невозможным .

Пример: В мешке лежат три картофелины.

Опыт – изъятие овоща из мешка.

Достоверное событие – изъятие картофелины.

Невозможное событие – изъятие кабачка.

Классическое определение вероятности

Равновозможными называют события, если в результате опыта ни одно из них не имеет большую возможность появления, чем другие.

Примеры: 1) Опыт - выбрасывается монета.

Выпадение орла и выпадение решки –

равновозможные события.

2) В урне лежат три шара. Два белых и синий.

Опыт – извлечение шара.

События – извлекли синий шар и извлекли

белый шар - неравновозможны.

Появление белого шара имеет больше шансов..

Классическое определение вероятности

Несовместимыми (несовместными) называют события, если наступление одного из них исключает наступление других.

Пример: 1) В результате одного выбрасывания выпадает

орел (событие А) или решка (событие В).

События А и В - несовместны.

2) В результате двух выбрасываний выпадает

орел (событие А) или решка (событие В).

События А и В - совместны. Выпадение орла в первый раз

не исключает выпадение решки во второй

Классическое определение вероятности

Полной группой событий называется множество всех событий рассматриваемого опыта, одно из которых обязательно произойдет, а любые два других несовместны.

События образующие полную группу называют элементарными.

Пример: 1) Опыт – один раз выбрасывается монета.

Элементарные события: выпадение орла

и выпадение решки образуют полную группу.

Классическое определение вероятности

Вероятностью случайного события А называется отношение числа элементарных событий, которые благоприятствуют этому событию, к общему числу всех элементарных событий, входящих в данную группу .

P(A) = m/n

Приложение 1

Общая схема решения вероятностных задач (единичные испытания)

• Определить, в чем состоит случайный эксперимент.
• Определить, какие в эксперименте элементарные события.
• Убедиться, что события равновероятны.
• Найти общее число элементарных исходов (n).
• Определить, какие элементарные события благоприятствуют событию А, найти их количество (m).
• Найти вероятность события А по формуле P(A)=m/n

13.10.16

Для конечных множеств событий при нахождении m и n широко используют правила комбинаторики.

Задача №1: Сколько двузначных чисел можно

составить используя цифры 7; 8; 9

(цифры могут повторяться)?

В данном случае легко перебрать все комбинации.

77

78

79

88

87

89

99

97

98

9 вариантов

Задача №2: Сколько пятизначных можно

составить используя цифры 7; 8; 9

(цифры могут повторяться)?

Как видим, в этой задаче перебор довольно затруднителен.

Решим задачу иначе.

На первом месте может стоять

любая из трех цифр – 3 варианта.

На втором месте может стоять

любая из трех цифр – 3 варианта.

На третьем месте может стоять

любая из трех цифр – 3 варианта.

На четвертом месте может стоять

любая из трех цифр – 3 варианта.

На пятом месте может стоять

любая из трех цифр – 3 варианта.

Комбинаторное правило умножения

Задачи открытого банка

Задача 1.Ученика попросили назвать число от 1 до 100. Какова вероятность того, что он назовёт число 56?

Число возможных исходов - 100 (сто чисел). Верно названное число одно. Это 56, значит благоприятный исход один. Вероятность того, что он назовёт число 56 будет один к ста или 0,01.

Ответ: 0,01

Задача 2. Ученика попросили назвать число от 1 до 100. Какова вероятность того, что он назовёт число кратное пяти?

Число возможных исходов 100 (сто чисел). Чисел кратных пяти двадцать (перечислим):5,10,15,20,25,30,35,40,45,50,55,60,65,70,75,80,85,90,95,100. То есть число благоприятных исходов 20. Вероятность того, что ученик назовёт число кратное пяти равна 20 к 100 или 20/100=0,2.

Ответ: 0,2

Задача 3. Ученика попросили назвать число от 1 до 100. Какова вероятность того, что он назовёт число, принадлежащее промежутку от 5 до 20 включительно?

Число возможных исходов - 100. Число благоприятных исходов - 16: это числа от 5 до 20 (5,6…..19,20), причём 5 и 20 входят в промежуток (в условии сказано «от 5 до 20 включительно»). Искомая вероятность равна 16/100.

Ответ: 0,16

Задача 4. Валя выбирает трёхзначное число. Найдите вероятность того, что оно делится на 51.

Число возможных исходов - это количество трёхзначных чисел. Их существует от 100 до 999, быстрее всего их можно посчитать так: 1000-1-99=900 (исключаем тысячу и числа от 1 до 99). То есть число всевозможных исходов: 900. Найдем, сколько трехзначных чисел делится на 51. Если мы поделим 999 - самое большое трехзначное число - на 51, то получим приблизительно 19 целых пятьдесят восемь сотых. То есть в 999 вмещается 19 чисел, кратных 51. Но среди них есть и само число 51, которое не является трехзначным. А значит трехзначных чисел, делящихся на 51 - 18.

Число благоприятных исходов 18. Вероятность искомого события равна 18 к 900, или 18/900=0,02.

Ответ: 0,02

Задача 5. Ве­ро­ят­ность того, что на те­сти­ро­ва­нии по ма­те­ма­ти­ке уча­щий­ся П. верно решит боль­ше 7 задач, равна 0,78. Ве­ро­ят­ность того, что П. верно решит боль­ше 6 задач, равна 0,89. Най­ди­те ве­ро­ят­ность того, что П. верно решит ровно 7 задач.

Рас­смот­рим со­бы­тия A = «уча­щий­ся решит 7 задач» и В = «уча­щий­ся решит боль­ше 7 задач». Их сумма — со­бы­тие A + B = «уча­щий­ся решит боль­ше 6 задач». Со­бы­тия A и В не­сов­мест­ные, ве­ро­ят­ность их суммы равна сумме ве­ро­ят­но­стей этих со­бы­тий:

P(A + B) = P(A) + P(B).

Тогда, ис­поль­зуя дан­ные за­да­чи, по­лу­ча­ем: 0,89 = P(A) + 0,78, от­ку­да P(A) = 0,89 − 0,78 = 0,11.

Ответ: 0,11

Задача 6. Если гросс­мей­стер  А  иг­ра­ет бе­лы­ми, то он вы­иг­ры­ва­ет у гросс­мей­сте­ра  Б  с ве­ро­ят­но­стью 0,5. Если  А  иг­ра­ет чер­ны­ми,  то  А  вы­иг­ры­ва­ет у  Б  с ве­ро­ят­но­стью 0,3. Гросс­мей­сте­ры  А  и  Б  иг­ра­ют две пар­тии, при­чем во вто­рой пар­тии ме­ня­ют цвет фигур. Най­ди­те ве­ро­ят­ность того, что  А  вы­иг­ра­ет оба раза.

Воз­мож­ность вы­иг­рать первую и вто­рую пар­тию не за­ви­сят друг от друга. Ве­ро­ят­ность про­из­ве­де­ния не­за­ви­си­мых со­бы­тий равна про­из­ве­де­нию их ве­ро­ят­но­стей: 0,5 · 0,3 = 0,15.

Ответ: 0,15 .

Задача 7. В клас­се 21 уча­щий­ся, среди них два друга — Вадим и Олег. Класс слу­чай­ным об­ра­зом раз­би­ва­ют на 3 рав­ные груп­пы. Най­ди­те ве­ро­ят­ность того, что Вадим и Олег ока­жут­ся в одной груп­пе .

В клас­се 21 уча­щий­ся. 3 рав­ные груп­пы - это груп­пы по 7 че­ло­век. Пусть Вадим на­хо­дит­ся в одной из трех групп. Тогда для Олега в груп­пе Ва­ди­ма оста­ет­ся 6 мест из 20 воз­мож­ных. Таким об­ра­зом, ве­ро­ят­ность того, что Вадим и Олег ока­жут­ся в одной груп­пе:  6 из 20

Ответ: 0,3.

Задача 8. В фирме такси в данный момент свободно 10 машин: 5 чёрных, 1 жёлтая и 4 зелёных. На вызов выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.

Возможное число исходов - 10. Число благоприятных исходов - 1 (жёлтая машина одна). Искомая вероятность равна 1 к 10 или 0,1.

Ответ: 0,1

Задача 9. Ве­ро­ят­ность того, что новый элек­три­че­ский чай­ник про­слу­жит боль­ше года, равна 0,93. Ве­ро­ят­ность того, что он про­слу­жит боль­ше двух лет, равна 0,87. Най­ди­те ве­ро­ят­ность того, что он про­слу­жит мень­ше двух лет, но боль­ше года .

Пусть A = «чай­ник про­слу­жит боль­ше года, но мень­ше двух лет», В = «чай­ник про­слу­жит боль­ше двух лет», С = «чай­ник про­слу­жит ровно два года», тогда A + B + С = «чай­ник про­слу­жит боль­ше года».

Со­бы­тия A, В и С не­сов­мест­ные, ве­ро­ят­ность их суммы равна сумме ве­ро­ят­но­стей этих со­бы­тий. Ве­ро­ят­ность со­бы­тия С, со­сто­я­ще­го в том, что чай­ник вый­дет из строя ровно через два года — стро­го в тот же день, час и се­кун­ду — равна нулю. Тогда:

  P(A + B+ С) = P(A) + P(B)+ P(С)= P(A) + P(B),

  от­ку­да, ис­поль­зуя дан­ные из усло­вия, по­лу­ча­ем

  0,93 = P(A) + 0,87.

Тем самым, для ис­ко­мой ве­ро­ят­но­сти имеем:

P(A) = 0,93 − 0,87 = 0,06.

Ответ: 0,06.

Задача 10. У Вити в ко­пил­ке лежит 12 рублёвых, 6 двух­рублёвых, 4 пя­ти­рублёвых и 3 де­ся­ти­рублёвых мо­не­ты. Витя на­у­гад достаёт из ко­пил­ки одну мо­не­ту. Най­ди­те ве­ро­ят­ность того, что остав­ша­я­ся в ко­пил­ке сумма со­ста­вит более 70 руб­лей .

У Вити в ко­пил­ке лежит 12 + 6 + 4 + 3 = 25 монет на сумму 12 + 12 + 20 + 30 = 74 рубля. Боль­ше 70 руб­лей оста­нет­ся, если до­стать из ко­пил­ки либо рублёвую, либо двух­рублёвую мо­не­ту. Ис­ко­мая ве­ро­ят­ность равна 18 : 25 = 0,72.

Ответ: 0,72.

Задача 11. В чемпионате по гимнастике участвуют 50 спортсменок: 24 из США, 13 из Мексики, остальные — из Канады. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Канады.

Благоприятное событие А: первой выступает

спортсменка из Канады

К-во всех событий группы: n=?

К-во благоприятных

событий: m=?

Соответствует количеству всех гимнасток.

n=50

Соответствует

количеству

гимнасток

из Канады.

m=50-(24+13)=13

13.10.16

Задача 12. Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений — по одному от каждой страны. В первый день 8 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?

Выясним, как распределятся выступления по дням:

1 день – 8 выступлений, остальные поровну, значит по 18 выступлений в день.

2 день - 18 выступлений,

3 день – 18 выступлений,

4 день – 18 выступлений,

5 день – 18 выступлений

Вероятность, что выступление представителя России состоится в третий день конкурса, равна 18 к 80 или 18/80=0,225.

Ответ: 0,225

Задача 13. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?

В данном случае нужно поставить себя на место Руслана Орлова.

Он будет играть кем-то из 25 спортсменов (на чемпионат приехали Руслан и ещё 25 спортсменов), значит возможных исходов 25. Из них осталось 9 спортсменов из России. Это и есть число благоприятных исходов. Вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России 9 к 25 или 0,36.

Задача 14. В среднем из 1400 садовых насосов, поступивших в продажу, 14 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.

Благоприятное событие А: выбранный насос

не подтекает .

К-во всех событий группы: n=?

Соответствует количеству всех насосов.

n=1400

К-во благоприятных

событий: m=?

Соответствует

количеству

исправных

насосов

m=1400-14=1386

13.10.16

Задача 15 . Фабрика выпускает сумки. В среднем на 190 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых .

Благоприятное событие А: купленная сумка

оказалась качественной.

К-во всех событий группы: n=?

Соответствует количеству всех сумок.

n=190+8

К-во благоприятных

событий: m=?

Соответствует

количеству

качественных

сумок.

m=190

13.10.16

• В кармане у Пети было 4 монеты по рублю и 2 монеты по 5 рублей.
• Петя, не глядя, переложил какие-то три монеты в другой карман.
• Найдите вероятность того, что пятирублевые монеты лежат в
• разных карманах.

• В кармане у Пети было 4 монеты по рублю и 2 монеты по 5 рублей.
• Петя, не глядя, переложил какие-то три монеты в другой карман.
• Найдите вероятность того, что обе пятирублевые монеты лежат в
• одном кармане.

• Вероятность и правило произведения.
• Решение:
• Всего 6 монет. Возможны варианты перекладывания:
• 1 карман 2 карман
• 5 1 1 5 1 1
• 1 1 5 1 1 5
• 1 5 1 1 5 1
• Р = ( 2/6 * 4/5 * 3/4 ) * 3 =3/5 = 0,6
• « 5 » « 1 » « 1 »

Задача 16. В кармане у Пети было 4 монеты по рублю и 2 монеты по 5 рублей.

Петя, не глядя, переложил какие-то три монеты в другой карман.

Найдите вероятность того, что пятирублевые монеты лежат в

разных карманах.

• Вероятность и правило произведения.
• Решение:
• Всего 6 монет. Возможны варианты перекладывания:
• 1 карман 2 карман
• 5 5 1 1 1 1
• 5 1 5 1 1 1 ИЛИ наоборот
• 1 5 5 1 1 1
• Р = ( 2/6 * 1/5 * 4/4 ) * 2 = 2/5 = 0,4
• « 5 » « 5 » « 1 »

Задача 17. В кармане у Пети было 4 монеты по рублю и 2 монеты по 5 рублей.

Петя, не глядя, переложил какие-то три монеты в другой карман.

Найдите вероятность того, что обе пятирублевые монеты лежат в

одном кармане .

Задача 18. При двукратном бросании игрального кубика в сумме вып ал о 6 очков. Найдите вероятность того, что первый раз выпало меньше трёх очков.

Сумму в шесть очков можно получить следующими способами (переберём варианты): 1+5, 2+4, 3+3, 4+2, 5+1 - всего их пять, это и есть число возможных исходов. Из представленных вариантов также видно, что менее трёх очков при первом броске может выпасть только в двух случаях. Искомая вероятность равна 2 к 5 или 0,4.

Ответ: 0,4

Задача 19. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпад ет 7 очков. Результат округлите до сотых .

Опыт: бросают три игральные кости .

Благоприятное событие А: в сумме выпало 7 очков.

К-во благоприятных

событий m=?

К-во всех событий группы n=?

1-я кость - 6 вариантов

2-я кость - 6 вариантов

3-я кость - 6 вариантов

511

151

115

331

313

133

223

232

322

142

214

241

412

421

124

13.10.16

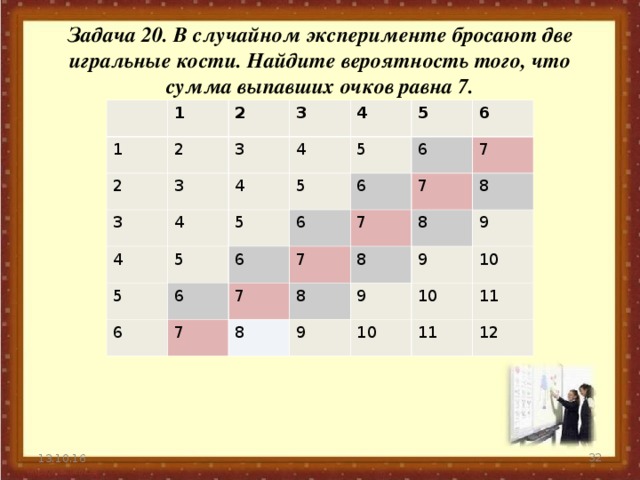
Задача 20. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что сумма выпавших очков равна 7.

1

1

2

2

2

3

3

3

3

4

4

4

4

4

5

5

5

5

5

5

6

6

6

6

6

6

6

7

7

7

7

7

7

8

8

8

8

8

9

9

9

9

10

10

10

11

11

12

13.10.16

Задача 21. При двукратном бросании игрального кубика в сумме выпало 6 очков. Найдите вероятность того, что первый раз выпало меньше трёх очков.

Сумму в шесть очков можно получить следующими способами (переберём варианты):

1 кубик 2 кубик

1 5

2 4

3 3

4 2

5 1

- всего их пять, это и есть число возможных исходов. Из представленных вариантов также видно, что менее трёх очков при первом броске может выпасть только в двух случаях. Искомая вероятность равна 2 к 5 или 0,4.

Ответ: 0,4

Задача 22. Наташа и Вика играют в кости. Они бросают игральную кость по одному разу. Выигрывает тот, кто выбросил больше очков. Если очков выпало поровну, то наступает ничья. В сумме вып ал о 8 очков. Найдите вероятность того, что Наташа выиграла .

1

1

2

2

11

3

21

12

3

4

31

22

13

4

23

5

41

14

5

32

6

24

42

6

15

33

51

61

43

25

52

34

16

26

44

35

53

62

63

45

54

36

46

55

64

65

56

66

Всего 5исходов. Благоприятных исходов – 2. Р = 2/5

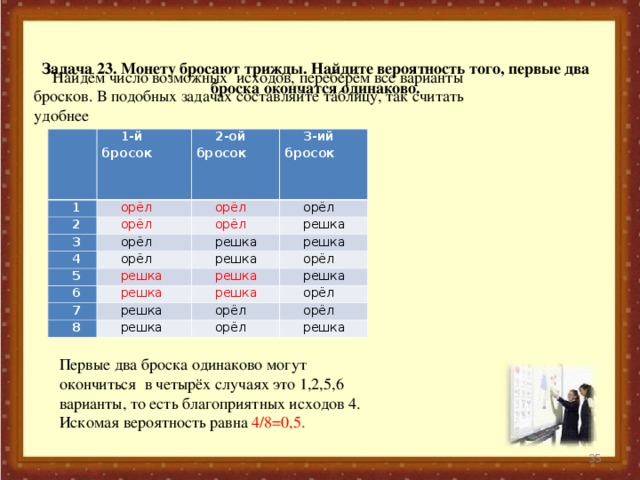
Найдём число возможных исходов, переберём все варианты бросков. В подобных задачах составляйте таблицу, так считать удобнее

Задача 23. Монету бросают трижды. Найдите вероятность того, первые два броска окончатся одинаково.

1

1-й бросок

орёл

2-ой бросок

2

3-ий бросок

орёл

орёл

3

орёл

орёл

4

орёл

5

решка

орёл

решка

решка

решка

решка

6

7

орёл

решка

решка

решка

решка

решка

8

орёл

орёл

решка

орёл

орёл

решка

Первые два броска одинаково могут окончиться в четырёх случаях это 1,2,5,6 варианты, то есть благоприятных исходов 4. Искомая вероятность равна 4/8=0,5.

Задача 24. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел не выпадет ни разу.

В данной задаче составляется та же таблица, что и предыдущей. Орёл не выпадет ни разу только в одном варианте из восьми (пятый вариант). Искомая вероятность равна 1 к 8 или 0,125.

Ответ: 0,125

Задача 25. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что сумма выпавших очков равна 7.

1

1

2

2

2

3

3

3

3

4

4

4

4

4

5

5

5

5

5

5

6

6

6

6

6

6

6

7

7

7

7

7

7

8

8

8

8

8

9

9

9

9

10

10

10

11

11

12

Всего исходов – 36

Благоприятных исходов – 6

Р=6/36=1/6

Задача 26. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орел не выпадет ни разу .

Условие можно трактовать так: какова вероятность того,

что все четыре раза выпадет решка?

К-во всех событий группы n=?

1-й раз - 2 варианта

2-й раз - 2 варианта

3-й раз - 2 варианта

4-й раз - 2 варианта

К-во благоприятных

событий m=?

m=1

Четыре раза выпала

решка .

13.10.16