Вероятность в ЕГЭ

МБОУ «Школа №91 с УИОП»

Вероятность в ЕГЭ

Основные типы задач

Калистратова И. А.

г. Нижний Новгород

Типы

• Классическое определение вероятности

• Вероятности сложных событий

• Перекладывание монет
• Погода
• Мишени
• Игральный кубик
• Торговые автоматы, фонари
• Рисунки, чертежи
• Меньше, больше
• Жребий
• Проценты

В классе 26 учащихся, среди них два друга — Андрей и Сергей. Учащихся случайным образом разбивают на 2 равные группы. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе.

Решение.

Пусть один из друзей находится в некоторой группе. Вместе с ним в группе окажутся 12 человек из 25 оставшихся одноклассников.

Вероятность того, что второй друг окажется среди этих 12 человек, равна 12 : 25=0,48.

Ответ: 0,48.

На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной?

Решение.

На клавиатуре телефона 10 цифр, из них 5 чётных: 0, 2, 4, 6, 8. Поэтому вероятность того, что случайно будет нажата четная цифра, равна 5:10 = 0,5.

Ответ: 0,5.

За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.

Решение.

Пусть первой за стол сядет девочка, рядом с ней есть два места, на каждое из которых может сесть 8 человек, из которых только одна девочка. Таким образом, вероятность, что девочки будут сидеть рядом равна 2: 8 =0,25

Ответ: 0,25.

В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.

Решение.

Равновозможных 4 исхода эксперимента: орел-орел, орел-решка, решка-орел, решка-решка. Орел выпадает ровно один раз в двух случаях: орел-решка и решка-орел. Поэтому вероятность того, что орел выпадет ровно 1 раз, равна 2: 4=0,5

Ответ: 0,5.

Перекладывание монет

Для задач о подбрасывании монеты существуют два основных метода решения, один - по формуле классической вероятности (фактически переборный метод, доступный даже школьникам), второй - по формуле Бернулли

В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно два раза.

ООО, ООР, ОРО, ОРР, РОО, РОР, РРО, РРР

  n=8 m=3(ООР, ОРО, РОО)

P=m/n=3/8=0,375

Ответ: 0,375.

Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Сапфир» играет три матча с разными командами. Найдите вероятность того, что в этих матчах команда «Сапфир» начнёт игру с мячом не более одного раза.

Решение. Обозначим «Р» ту сторону монеты, которая отвечает за выигрыш жребия «Сапфиром», другую сторону монеты обозначим «О». Тогда благоприятных комбинаций четыре: ООО, ООР, ОРО, РОО, а всего комбинаций 8: ООО, ООР, ОРО, ОРР, РОО, РОР, РРО, РРР. Тем самым, искомая вероятность равна:

Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Химик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Химик» выиграет жребий ровно два раза.

Решение. Обозначим «Р» ту сторону монеты, которая отвечает за выигрыш жребия «Химика», другую сторону монеты обозначим «О». Тогда благоприятных комбинаций три: РРО, РОР, ОРР, а всего комбинаций 8: ООО, ООР, ОРО, ОРР, РОО, РОР, РРО, РРР. Тем самым, искомая вероятность равна:

Симметричную монету бросают 16 раз. Во сколько раз вероятность события «выпадет ровно 8 орлов» больше вероятности события «выпадет ровно 7 орлов»?

Решение. По ф. Бернулли найдём вероятность события А (при 16 бросаниях выпадет ровно 8 орлов):

Аналогично найдем вероятность события B (при 16 бросаниях выпадет ровно 7 орлов):

Тогда:

Ответ: 1,125

В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел не выпадет ни разу.

Подставляем n=3,k=0 и получаем 

P=C 0 3 ⋅(1/2) 3 =1⋅1/8=1/8=0.125

События называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании.

P(A+B)=P(A)+P(B)-P(A*B)

События называются несовместными, если появление одного из них исключает появление другого в одном и том же испытании.

P(A+B)=P(A)+P(B)

Два события называются противоположными, если в данном испытании они несовместимы и одно из них обязательно происходит.

P(A)=1-P(B)

Два случайных события называются независимыми, если наступление одного из них не изменяет вероятность наступления другого.

P(A*B)=P(A)*P(B)

В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.

Решение: Для погоды на 4, 5 и 6 июля есть 4 варианта: ХХО, ХОО, ОХО, ООО (здесь Х  — хорошая, О  — отличная погода). Найдем вероятности наступления такой погоды:

P(XXO) = 0,8·0,8·0,2 = 0,128;

P(XOO) = 0,8·0,2·0,8 = 0,128;

P(OXO) = 0,2·0,2·0,2 = 0,008;

P(OOO) = 0,2·0,8·0,8 = 0,128.

Указанные события несовместные, вероятность их суммы равна сумме вероятностей этих событий:

P(ХХО) + P(ХОО) + P(ОХО) + P(ООО)  =  0,128 + 0,128 + 0,008 + 0,128  =  0,392.

Ответ:0,392

В Волшебной стране бывает два типа погоды: дождливая и солнечная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,7 погода завтра будет такой же, как и сегодня. Сегодня, 3 мая, погода в стране солнечная. Найдите вероятность того, что 5 мая в стране будет дождливая погода.

Решение: Для погоды на 4 и 5 мая есть 2 варианта: СД, ДД (здесь С-солнечная ,Д-дождливая). Найдем вероятности наступления такой погоды:

P(СД) = 0,7·0,3 = 0,21;

P(ДД) = 0,3·0,7 = 0,21;

Указанные события несовместные, вероятность их суммы равна сумме вероятностей этих событий:

P(СД) + P(ДД)   =  0,21 + 0,21  =  0,42

Ответ: 0,42

Задачи про стрелков, которые делают выстрелы по целям (или мишеням), причем вероятности попаданий для каждого стрелка обычно заданы, а нужно найти вероятность ровно одного попадания, или не более двух попаданий, или всех трех и так далее, в зависимости от конкретной задачи.

Основной метод решения подобных задач - использование теорем о сложении и умножении вероятностей, который мы и разберем на примерах ниже.

Стрелок при каждом выстреле поражает мишень с вероятностью 0,3, независимо от результатов предыдущих выстрелов. Какова вероятность того, что он поразит мишень, сделав не более 3 выстрелов?

Пусть:

A  — событие, состоящее в том, что мишень поражена стрелком с первого выстрела,

B  — событие, состоящее в том, что первый раз стрелок промахнулся, а со второго выстрела поразил мишень,

С  — событие, состоящее в том, что первые два раза стрелок промахнулся, а с третьего выстрела поразил мишень.

P(A) = 0,3.

P(B)  =  0,3·0,7 = 0,21.

Ответ: 0,657.

P(C)  =  0,3·0,7·0,7  =  0,147.

P(A + B+ С) = P(A) + P(B) + P(С) = 0,3 + 0,21 + 0,147 = 0,657.

Два стрелка, для которых вероятности попадания в мишень равны соответственно 0,7 и 0,8, производят по одному выстрелу. Найти вероятность того, что мишень поражена только один раз.

Пусть вероятность, что первый попал p1=0.8; промазал q1=1-p1=0.2

Вероятность, что второй попал p2=0.7; промазал q2=1-p2=0.3

Тогда вероятность что в мишень попал только один:

P=p1* q2+p2*q1=0.8*0.3+0.7+0.2=0.38

Ответ: 0.38

Два стрелка, для которых вероятности попадания в мишень равны соответственно 0,7 и 0,8, производят по одному выстрелу. Найти вероятность того, что мишень поражена дважды.

Попал первый стрелок: p1 = 0.7

Попал второй стрелок: p2 = 0.8

Вероятность, что они оба попадут в мишень:

P= p1*p2= 0.7*0.8 = 0.56

Ответ: 0,56

Решение задач с использованием формулы Бернулли:

Стрелок стреляет по одному разу по каждой из пяти одинаковых мишеней. Вероятность поразить мишень каждым отдельным выстрелом равна 0,8. Во сколько раз вероятность события «стрелок поразит ровно четыре мишени» больше вероятности события «стрелок поразит ровно три мишени»?

Решение:

0,8 - попадание в мишень с первого раза

1-0,8 = 0,2 - промах

- поразит ровно 4 раза

- поразит ровно 3 раза

Ответ: 2

Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень даётся не более двух выстрелов, и известно, что вероятность поразить мишень каждым отдельным выстрелом равна 0,8. Во сколько раз вероятность события «стрелок поразит ровно пять мишеней» больше вероятности события «стрелок поразит ровно четыре мишени»?

Решение: 0,8+0,2*0,8=0,96 - попасть в мишень с первого или второго выстрела

1-0,96=0,04 - стрелок не попадёт в мишень с двух выстрелов

«стрелок поразит ровно пять мишеней» равна P 5 (5) = 0,96 5 .

• - стрелок поразит ровно четыре мишени

- искомое отношение вероятностей

Ответ: 4,8

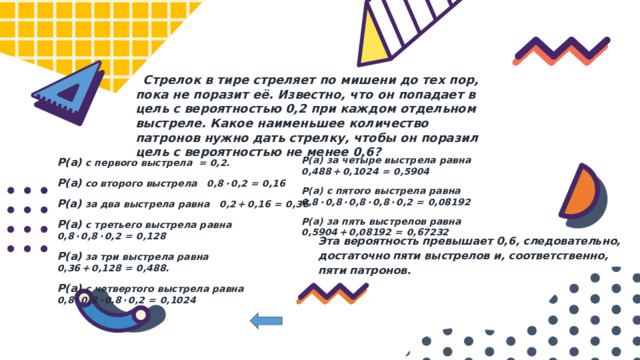
Стрелок в тире стреляет по мишени до тех пор, пока не поразит её. Известно, что он попадает в цель с вероятностью 0,2 при каждом отдельном выстреле. Какое наименьшее количество патронов нужно дать стрелку, чтобы он поразил цель с вероятностью не менее 0,6?

Р(а) за четыре выстрела равна 0,488 + 0,1024  =  0,5904

Р(а) с пятого выстрела равна 0,8 · 0,8 · 0,8 · 0,8 · 0,2  =  0,08192

Р(а) за пять выстрелов равна 0,5904 + 0,08192  =  0,67232

Р(а) с первого выстрела = 0,2.

Р(а) со второго выстрела 0,8 · 0,2  =  0,16

Р(а) за два выстрела равна 0,2 + 0,16  =  0,36

Р(а) с третьего выстрела равна 0,8 · 0,8 · 0,2  =  0,128

Р(а) за три выстрела равна 0,36 + 0,128  =  0,488.

Р(а) с четвертого выстрела равна 0,8 · 0,8 · 0,8 · 0,2  =  0,1024

Эта вероятность превышает 0,6, следовательно, достаточно пяти выстрелов и, соответственно, пяти патронов.

При двукратном бросании кости в сумме выпало 9 очков. Какова вероятность того, что хотя бы раз выпало 5 очков?

Решение: При двукратном бросании игральной кости 9 очков может получится только в четырёх случаях: 6 + 3, 5 + 4, 4 + 5 и 3 + 6. При этом 5 очков выпадало в двух из этих случаев (все эти случаи равновероятны). Значит, вероятность того, что хотя бы раз выпало 5 очков равна.

Ответ: 0,5.

Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 6. Какова вероятность того, что для этого потребовалось два броска? Ответ округлите до сотых.

Решение:

Найдём исходы, когда за 2 броска НЕ набралось более 6 очков:

1+1;1+2;1+3;1+4;1+5;2+1;2+2;2+3;2+4;3+1;3+2;3+3;4+1;4+2;5+1 - всего 15 исходов.

При 2в степени х бросках всего 6⋅6=36 исходов. Тогда в 36−15=21 исходах получили более 6 за 2 броска:

Р(А)=21/36=0,5833…≈0,58

Ответ: 0,58

Марина и Дина бросают кубик по одному разу. Выигрывает та девочка, у которой выпадет больше очков. Первой кубик бросила Марина, у нее выпало 3 очка. Найдите вероятность того, что Дина выиграет.

Решение:

Кубик бросается один раз. Марина уже бросила кубик и у нее выпало 3 очка. Дина может выиграть у Марины, если при бросании игрального кубика выпадут числа 4, 5 или 6. Всего возможных исходов 6. Следовательно, вероятность того, что Дина выиграет, равна

3/6=1/2=0,5

Ответ: 0,5.

Бросают 3 игральные кости. Найдите вероятность того, что в сумме выпало 15 очков.

Решение:

Очевидно, что всего таких троек чисел будет n=6⋅6⋅6=216

Подберем такие исходы, которые дают в сумме 15 очков.

(3,6,6),(6,3,6),(6,6,3),(4,5,6),(4,6,5),(5,4,6),(6,5,4),(5,6,4),(6,4,5),(5,5,5).

Всего их 10. Теперь найдём вероятность выпадения 15 очков.

Искомая вероятность: P=10/216=0,046

Ответ: 0,046

Игральную кость бросили два раза. Известно, что три очка

не выпали ни разу. Найдите при этом условии вероятность

События «сумма выпавших очков окажется равна 8».

Решение:

Условию, что при двукратном броске игральной кости три очка не выпали ни разу, соответствует 25 исходов (отмечены оранжевым цветом). Событию «сумма выпавших очков равна 8» соответствуют 3 из них (отмечены зелёным цветом). Значит, искомая вероятность равна:

Ответ: 0,12.

Игральную кость бросают дважды. Найдите вероятность того, что сумма двух выпавших чисел равна 4 или 7.

Решение:

Сумма двух выпавших чисел будет равна 4 в трех случаях(1 и 3, 3 и 1, 2 и 2) и 7 в шести случаях(1 и 6, 6 и 1, 2 и 5, 5 и 2, 3 и 4, 4 и 3), т. е. 9 благоприятных событий. А всего событий может быть 6 · 6 = 36, значит, вероятность равна:

Ответ: 0,25.

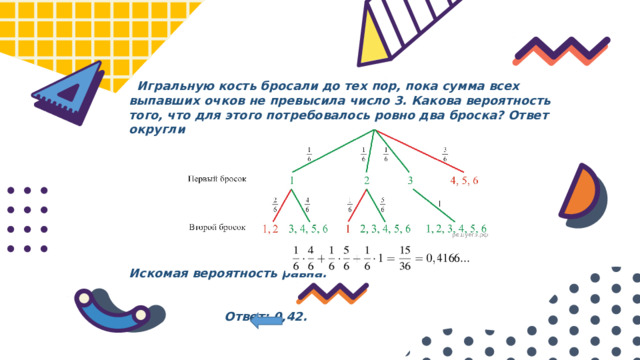
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 3. Какова вероятность того, что для этого потребовалось ровно два броска? Ответ округлите до сотых.

Искомая вероятность равна:

Ответ: 0,42.

В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в первом автомате закончится кофе, равна 0,35. Вероятность того, что кофе закончится во втором автомате, такая же. Вероятность того, что кофе закончится в двух автоматах, равна 0,16. Найдите вероятность того, что к концу дня кофе останется в двух автоматах.

Решение.

А = кофе закончится в первом автомате,

В = кофе закончится во втором автомате.

Тогда

A·B = кофе закончится в обоих автоматах,

A + B = кофе закончится хотя бы в одном автомате.

По условию P(A)  =  P(B)  =  0,3; P(A·B)  =  0,12.

События A и B совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения:

P(A + B)  =  P(A) + P(B) − P(A·B)  =  0,3 + 0,3 − 0,12  =  0,48.

Следовательно, вероятность противоположного события, состоящего в том, что кофе останется в обоих автоматах, равна 1 − 0,48  =  0,52.

В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах

Формула условной вероятности для двух событий A и B:

P(A|B) = P(A ∩ B) / P(B)

Здесь:

— P(A ∩ B) — вероятность одновременного наступления обоих событий A и B; — P(B) — вероятность наступления события B.

*Другими словами, условная вероятность того, что данное событие B уже произошло, равна вероятности пересечения A и B, деленной на вероятность события B.

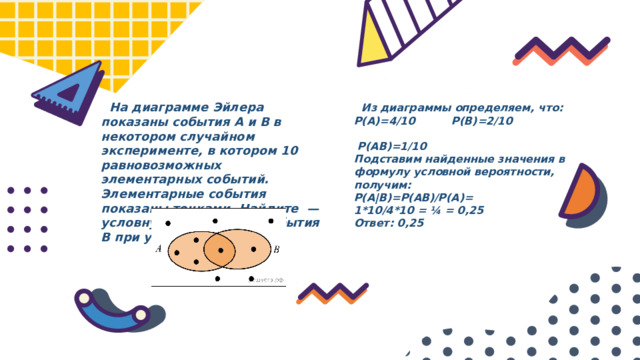
На диаграмме Эйлера показаны события A и B в некотором случайном эксперименте, в котором 10 равновозможных элементарных событий. Элементарные события показаны точками. Найдите — условную вероятность события B при условии A.

Из диаграммы определяем, что:

P(A)=4/10 P(B)=2/10

P(AB)=1/10

Подставим найденные значения в формулу условной вероятности, получим:

P(A|B)=P(AB)/P(A)=

1*10/4*10 = ¼ = 0,25

Ответ: 0,25

По рисунку находим вероятности элементарных событий a, b и c:

P(d)= 0,4* 0,7=0,2 8

P(c)= 0,3* 0,4=0,12

P(a)=P(b)= 0,6 * 0,5=0,3

На рисунке показано дерево некоторого случайного эксперимента. Событию A благоприятствуют элементарные события a, b и c, а событию B благоприятствуют элементарные события b, c и d. Найдите P(A|B) — условную вероятность события A при условии B.

По формуле условной вероятности:

P(A|B)=P(AB)/P(B)= 0,42/0,7 =0,6

Вероятность события A равна сумме вероятностей событий a, b и c:

P(A)=P(a)+P(b)+P(c) = 0,3+ 0,3+0,12 = 0,72

Вероятность события B равна сумме ввероятностей событий b, c и d:

P(B)=P(d)+P(b)+P(c) = 0,28+ 0,3+0,12 = 0,7

Вероятность произведения А и B равна сумме вероятностей событий b и c и c

P(AB)=P(b)+P(c)= 0,3+0,12 = 0,42

Ответ: 0,6.

На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу C.

На пути к выходу С паук встретит 4 развилки. На каждой из них он с вероятностью 0,5 может выбрать или путь, ведущий к выходу С, или другой путь. Это независимые события, вероятность их произведения (события, состоящего в том, что паук дойдет до выхода С) равна произведению вероятностей этих событий. Поэтому вероятность прийти к выходу С равна (0,5) 4   =  0,0625.

Ответ: 0,0625.

На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу A.

На пути к выходу A паук встретит 3 развилки. На каждой из них он с вероятностью 0,5 может выбрать или путь, ведущий к выходу A, или другой путь. Это независимые события, вероятность их произведения (события, состоящего в том, что паук дойдет до выхода A) равна произведению вероятностей этих событий. Поэтому вероятность прийти к выходу A равна (0,5) 3   =  0,125.

Ответ: 0,125

Вероятность того, что новый электрический чайник прослужит больше года равна 0,97. Вероятность того, что он прослужит более двух лет равна 0,89. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

Ответ: 0,08.

Вероятность того, что температура здорового человека в случайный момент времени окажется ниже чем 36,8°С равна 0,81. Найдите вероятность того, что в случайный момент времени о здорового человека температура окажется 36,8°С или выше.

Вероятность того, что на тестировании по биологии О. верно решит больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит 11 задач.

Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Статор» по очереди играет с командами «Ротор», «Мотор» и «Стартер». Найдите вероятность того, что «Статор» будет начинать только первую и последнюю игры.

Решение: Требуется найти вероятность произведения трех событий: «Статор» начинает первую игру, не начинает вторую игру, начинает третью игру. Вероятность произведения независимых событий равна произведению вероятностей этих событий. Вероятность каждого из них равна 0,5, откуда находим: 0,5·0,5·0,5  =  0,125.

Ответ: 0,125

Перед началом волейбольного матча капитаны команд тянут жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Мотор» по очереди играет с командами «Статор», «Стартер» и «Ротор». Найдите вероятность того, что «Мотор» будет начинать с мячом только вторую игру.

Решение: Требуется найти вероятность произведения трех событий: «Мотор» не начинает первую игру, начинает вторую игру, не начинает третью игру. Вероятность произведения независимых событий равна произведению вероятностей этих событий. Вероятность каждого из них равна 0,5, откуда находим: 0,5·0,5·0,5  =  0,125. 

Ответ: 0,125.

Агрофирма закупает куриные яйца только в двух домашних хозяйствах. Известно, что 5% яиц из первого хозяйства  — яйца высшей категории, а из второго хозяйства  — 30% яиц высшей категории. В этой агрофирме 15% яиц высшей категории. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

Решение.

Пусть событие A состоит в том, что яйцо имеет высшую категорию, события B 1 и B 2 состоят в том, что яйцо произведено в первом и втором хозяйствах соответственно. Тогда события и    — события, состоящие в том, что яйцо высшей категории произведено в первом и втором хозяйстве соответственно. По формуле полной вероятности, вероятность того, что будет куплено яйцо высшей категории, равна:

По условию эта вероятность равна 0,15, поэтому для вероятности того, что купленное яйцо произведено в первом хозяйстве имеем:

Ответ: 0,6.

Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая  — 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая  — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Решение: Вероятность того, что стекло сделано на первой фабрике и оно бракованное: 0,45 · 0,03  =  0,0135.Вероятность того, что стекло сделано на второй фабрике и оно бракованное: 0,55 · 0,01  =  0,0055.Поэтому по формуле полной вероятности вероятность того, что случайно купленное в магазине стекло окажется бракованным равна 0,0135 + 0,0055  =  0,019.

Ответ: 0,019.

На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до сотых.

Решение: Пусть завод произвел n тарелок. В продажу поступят все качественные тарелки и 20% не выявленных дефектных тарелок:

Поскольку качественных из них 0,9n, вероятность купить качественную тарелку равна

Округляя результат до сотых, получаем 0,98.

Ответ: 0,98. 

В городе 48 % взрослого населения  — мужчины. Пенсионеры составляют 12,6 % взрослого населения, причём доля пенсионеров среди женщин равна 15 %. Для социологического опроса выбран случайным образом мужчина, проживающий в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером».

Решение: Женщин среди взрослого населения 100 % − 48 %  =  52 %, среди взрослого населения 52 % · 0,15  =  7,8 % пенсионерок. Всего в городе 12,6 % пенсионеров, поэтому мужчин-пенсионеров 12,6 % − 7,8 %  =  4,8 % от взрослого населения города. Поскольку всего среди взрослого населения города 48 % мужчин и среди них 4,8 % пенсионеров, пенсионером является каждый десятый: Следовательно, вероятность того, что случайно выбранный мужчина окажется пенсионером равна 0,1. 

Ответ: 0,1.