Векторы в пространстве

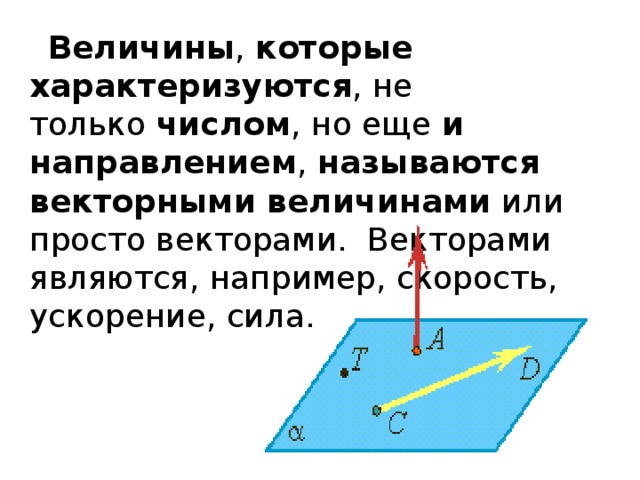
Величины, которые характеризуются, не только числом, но еще и направлением, называются векторными величинами или просто векторами.  Векторами являются, например, скорость, ускорение, сила.

Геометрически векторы изображаются направленными отрезками. 
Направленный отрезок называется вектором.
Вектор характеризуется следующими элементами:

1. начальной точкой (точкой приложения);
2. направлением; 
3. длиной («модулем вектора»).

От любой точки можно отложить вектор, равный данному, и притом только один, используя параллельный перенос.

Нулевой вектор - точка в пространстве. Начало и конец нулевого вектора совпадают, и он не имеет длины и направления.

Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор.

Векторы в пространстве

Величины ,  которые характеризуются , не только  числом , но еще  и направлением , называются векторными величинами  или просто векторами. Векторами являются, например, скорость, ускорение, сила.

Геометрически векторы изображаются направленными отрезками.  Направленный отрезок называется  вектором . Вектор характеризуется следующими элементами: 1) начальной точкой (точкой приложения); 2 )направлением;  3) длиной («модулем вектора»).

Если начало вектора — точка А, а его конец — точка В, то вектор обозначается   или  .

От любой точки можно отложить вектор, равный данному, и притом только один, используя параллельный перенос.

Нулевой вектор  - точка в пространстве. Начало и конец нулевого вектора совпадают, и он не имеет длины и направления.

Абсолютной величиной (или модулем)  вектора  называется длина отрезка, изображающего вектор. .

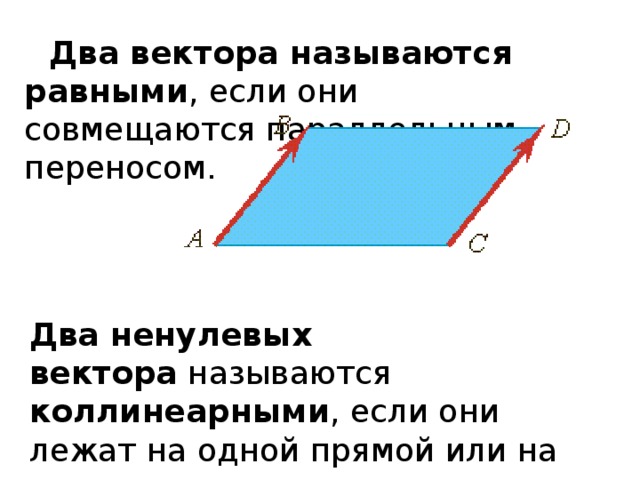
Два вектора называются равными , если они совмещаются параллельным переносом.

Два ненулевых вектора  называются 

коллинеарными , если они лежат на одной прямой или на параллельных прямых.

Если векторы  и  коллинеарны и их лучи сонаправлены, то векторы    называются сонаправленными .  Если векторы коллинеарны, а их лучи не являются сонаправленными, то в екторы называются противоположно направленными .  Нулевой вектор условились считать сонаправленным с любым вектором.  

коллинеарные векторы:

0, то векторы сонаправленные, если  k  " width="640"

Свойство коллинеарных векторов

Если векторы коллинеарны и не равны 0, то существует число  k  такое, что  . Причем если  k   0, то векторы сонаправленные, если  k  

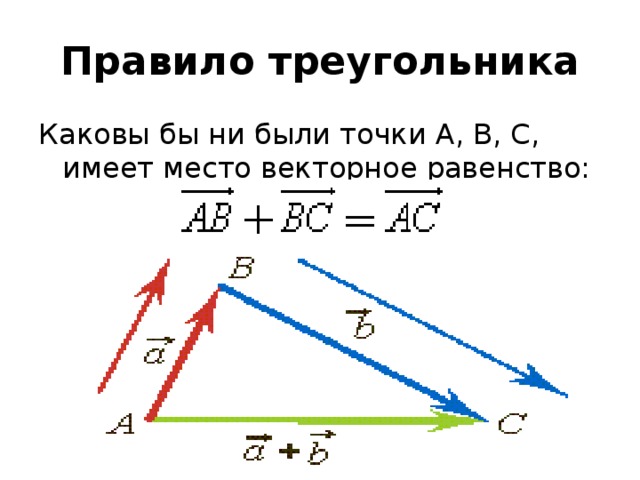
Правило треугольника

Каковы бы ни были точки А, В, С, имеет место векторное равенство:

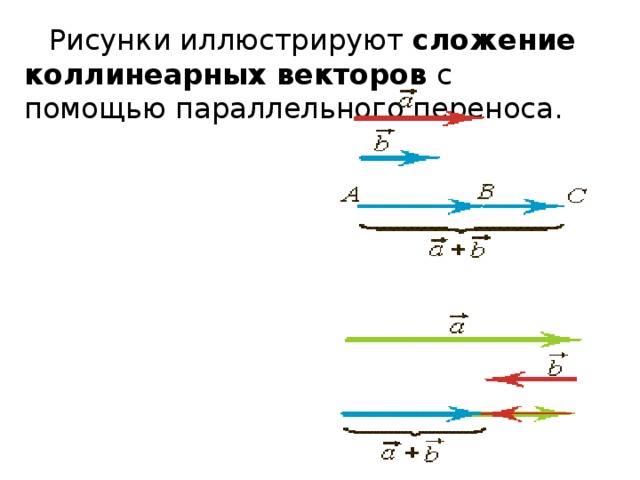
Рисунки иллюстрируют  сложение коллинеарных векторов  с помощью параллельного переноса.

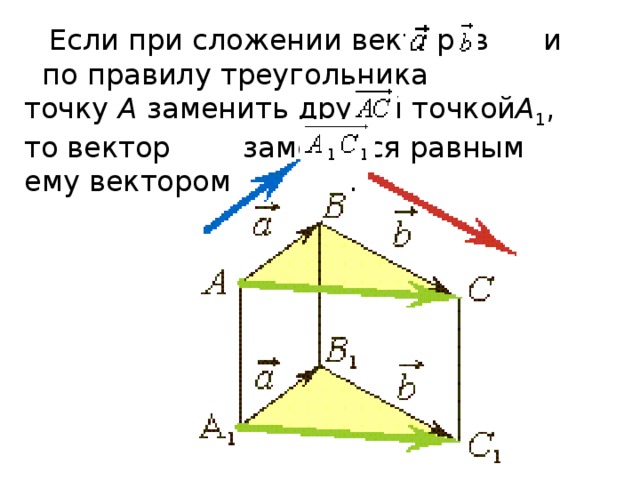
Если при сложении векторов   и   по правилу треугольника точку  А  заменить другой точкой А 1 , то вектор   заменится равным ему вектором   .

Диагональ параллелограмма есть сумма двух векторов 

  и  .

Правило параллелограмма

Если векторы   и   неколлинеарны, их можно отложить от одной точки, достроив затем параллелограмм. 

• Найти сумму векторов а(1; -2; 4) и

b(2; -3; 6)

• Даны точки А(0;0;1), В(2;3;5), С(6;2;3) и D(3;7;2). Вычислить длину вектора AB+CD.
• Найти длину вектора 3а, если

а(-5; 1; 12)

Свойства сложения векторов

Для любых векторов  заданных в пространстве, справедливы равенства

Переместительный закон

Сочетательный закон

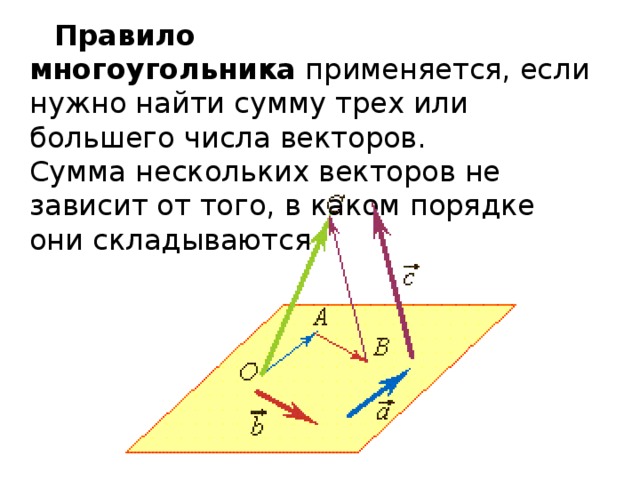
Правило многоугольника  применяется, если нужно найти сумму трех или большего числа векторов.  Сумма нескольких векторов не зависит от того, в каком порядке они складываются.

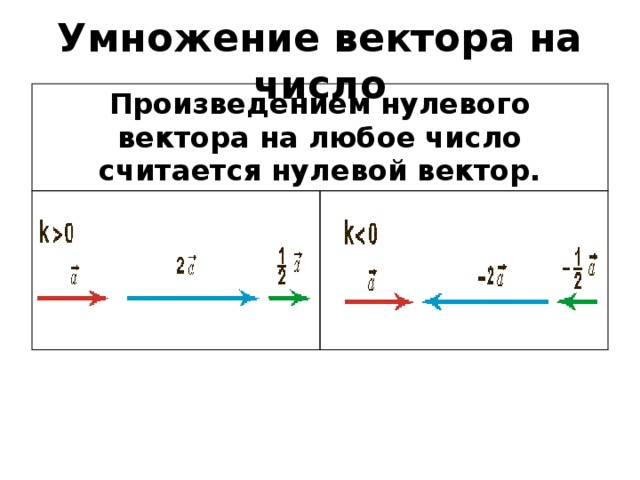
Умножение вектора на число

Произведением нулевого вектора на любое число считается нулевой вектор.

Свойства умножения вектора на число

Сочетательный закон

Первый распределительный закон

Второй распределительный закон

Компланарные векторы

• Векторы называются компланарными ,  если  при откладывании их от одной и той же точки  они будут лежать в одной плоскости .  Любые два вектора компланарны.
• Три вектора, среди которых имеются два коллинеарных, также компланарны.
• Три произвольных вектора могут быть компланарными (лежать в одной плоскости) или некомпланарными (не лежать в одной плоскости).

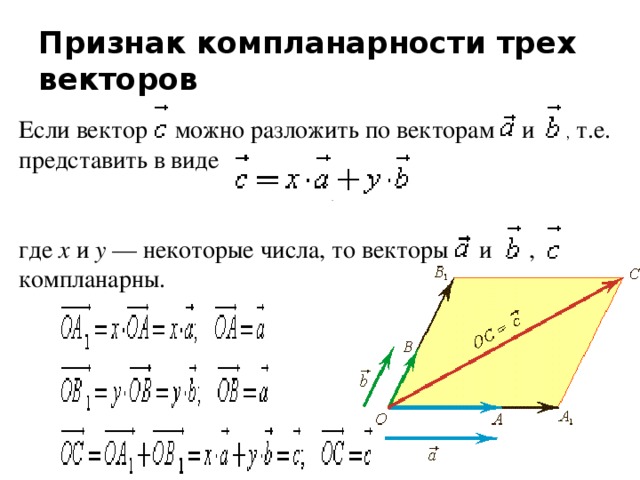
Признак компланарности трех векторов

Если вектор    можно разложить по векторам     и  , т.е. представить в виде

,

где  х  и  у  — некоторые числа, то векторы  и , компланарны.

Правило параллелепипеда

Сумма трех некомпланарных векторов равна вектору, изображаемому направленной диагональю параллелепипеда, построенному на этих векторах.