Цели урока:
Получить алгоритм умножения смешанных чисел, способствовать к его практическому использованию.
образовательная:Обеспечить условия для усвоения учащимися правила умножения смешанных чисел и для формирования умений в его применении. Проверить уровень усвоения изученной темы;
развивающая: Формирование внутренних процессов интеллектуального, личностного, эмоционального развития;
воспитательная:Содействовать воспитанию интереса к математике, аккуратности.
Тип урока: Урок изучения нового материала.
Структура урока:
I. Организационное начало.
II. Актуализация опорных знаний.
III. Постановка целей урока и мотивация изучения темы.
IV. Изучения нового материала.
V. Закрепление изученного материала.
VI. Проверка усвоения материала.
VII. Домашнее задание.
VIII. Рефлексия.
Методика и приемы используемые на уроке:технология проблемного обучения, исследовательский метод, интерактивная технология, практическая работа, наглядно - иллюстративный метод.
Оборудование:
1. Мультимедийный проектор
2. Экран
3. Раздаточный материал
Ход урока
I. Организационный момент. (2 мин)
Добрый день! Эпиграф нашего урока “О, сколько нам открытий чудных готовит просвещенья дух…”. А были ли открытия в вашей жизни? Что значат слова “Я сделал открытие”? Если человек своим трудолюбием, упорством достигает истины в чем - либо, то это и есть его открытие.
На сегодняшнем уроке мы тоже попытаемся совершить маленькое, но самостоятельное открытие. Для этого надо быть настойчивым и внимательным.
II. Актуализация опорных знаний. (5мин)
1) Устная работа.
2) № 1
Вычислите. Рядом с ответом поставьте букву с ленты ответов.
(Учитель проверяет, как выполняют примеры в тетради, если нужна помощь, помогает. )
Ребята, какое слово получилось. (МОЛОДЕЦ) Вот вы сами себя и оценили.
3) Фронтальное повторение теоретического материала.
- Что называют сокращением дроби?
- Какую дробь называют несократимой?
- К какому новому знаменателю можно привести данную дробь?
- Как найти дополнительный множитель?
- Какая дробь называется правильной (неправильной)?
- Как из неправильной дроби выделить целую часть?
- Как записать число в виде неправильной дроби?
- Как умножить дробь на натуральное число?
- Как выполнить умножение двух дробей?
- Свойства нуля при умножении?
4. Индивидуальная работа (во время устной работы)
Смотрите документ
3. Тест (у компьютера)
IV. Из истории дробей (2 - 3мин)
Рассказывает учащийся, подготовленный дома.
Дроби. Первое понятие дроби появилось в древнем Египте много веков назад. В русском языке это слово появилось лишь в VIII веке. Происходит слово “дробь” от слова “дробить, разбивать, ломать на части”. В первых учебниках дроби назывались “ломанные числа”. Современное обозначение дробей берет своё начало в древней Индии; дробная черта появилась в записи дробей лишь около 300 лет назад. Название “числитель” и “знаменатель” ввёл в употребление греческий монах учёный - математик Максим Пеануд. Долгое время дроби считались самым трудным разделом математики. У немцев даже сложилась поговорка “попасть в дроби”, что означает попасть в трудное положение.
Остальные дополняют ответ ученика.
Задача сегодняшнего урока – доказать, что дроби не смогут поставить вас в трудное положение.
V. Изучения нового материала (10 мин)
1) Подготовительная работа: представьте смешанные числа в виде неправильных дробей
2)Решите задачу. Какое расстояние пройдут туристы за 2 2/5 ч со скоростью 4 1/6 км/час?
Как найти расстояние? (Скорость умножить на время)
Ответ: 10 км.
- Возникла проблема. Как вы думаете, как можно перемножить смешанные числа? ( Все варианты решений выслушиваются, среди них выбирается самый рациональный, делаем вывод. ) Итак, ребята кто скажет алгоритм по которому мы сможем решать такие примеры. Прочитайте в учебнике на стр. 70 правило умножения смешанных чисел. Закончите решение задачи.
Чтобы умножить смешанные числа, надо…. Значит тема нашего сегодняшнего урока «Умножение смешанных чисел».
VI. Закрепление изученного (10 мин)
№ 446 (а - м) стр. 73
3 столбик - у доски «цепочкой» под руководством учителя с подробным комментированием.
2 столбик - у доски «цепочкой» с проговариванием правила умножения смешанных чисел.
1 столбик - самостоятельно, самопроверка, «цепочкой» на обратной стороне доски.
Весь материал - смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход


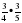
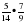


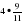
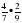
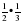
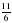
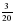
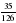
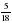
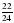
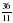
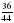
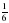
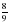

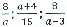 будут правильными,
будут правильными,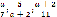 будут неправильными.
будут неправильными.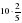 ; б)
; б)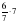 ; в)
; в)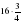 .
.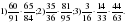
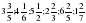
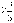 ч со скоростью
ч со скоростью 








 Урок математики "Умножение чисел" (90.77 КB)
Урок математики "Умножение чисел" (90.77 КB)
 0
0 482
482 42
42 Нравится
0
Нравится
0






