Урок математики 6 класс "Координатная плоскость"
Учитель: Нуркеева А.О
Предмет: Математика
Класс: 6 а
Тема урока: «Координатная плоскость»
Тип урока: Урок закрепление учебного материала
Цель: Формирование понятия «координатная плоскость», отработка навыков нахождения точки по ее координатам и определения координат точки, отмеченной на координатной плоскости.
Задачи:
Сформировать понятие прямоугольной системой координат на плоскости, сформировать представление о взаимно однозначном соответствии между точкой на координатной плоскости и ее координатами; отработать навыки нахождения точки по ее координатам и определения координат точки, отмеченной на координатной плоскости; расширить кругозор учащихся в историческом аспекте;
активизировать познавательную деятельность учащихся; развивать логическое мышление, умения анализировать, сравнивать, обобщать, выделять главное, делать выводы; развивать быстроту реакции, развивать память; развивать творческие способности учащихся; развивать умения учебного труда (умения работать в нужном темпе – писать, конспектировать, чертить); развивать умения и навыки применять математические знания к решению практических задач;
воспитывать у учащихся интерес к математике, к познанию; воспитывать аккуратность и культуру графических построений; воспитывать самостоятельность, волю и настойчивость, уверенность в своих силах, стремление к достижению результата.
Технологии:
Информационно-коммуникационные технологии;
Технология развития «критического мышления»;
Исследование в обучении;
Игровые технологии: обучающие игры;
Оборудование:
Компьютер, мультимедийный проектор, экран, презентация в программе Power Point, индивидуальный раздаточный материал для учащихся (карточки с координатами точек, образующих рисунок).
Ход урока:
Организационный момент.
Добрый день ребята! А хочу я ребята начать урок с притчи.
Лавка возможностей
«Однажды человеку приснился сон, будто он идет по городу и заходит в торговую лавку. Он долго ходит среди разнообразных экзотических заморских овощей и фруктов. Там есть весьма странные и необычные плоды и ягоды, даже и близко не похожие на те, что он ранее видел.
Одни привлекают его своими невероятными красками, другие манят предвкушением райского аромата, третьи — изысканными звуками, доносящимися из сердцевины фрукта. И, конечно же, каждый из людей выбирает то, что ему по душе, и часто оказывается, что именно это ему и необходимо.
Но как только человек брал в руки какой-нибудь фрукт, тот исчезал, оставляя на ладони крохотное семечко. Немало удивленный, он решил схитрить и подошел к хозяину лавки: «Дайте мне, пожалуйста, вон тот фрукт», — сказал он и показал на полку. Однако хозяин ответил ему: «Мы не торгуем плодами, мы торгуем семенами…».
Каждый сделает выводы сам, а к притче мы с Вами вернемся немного позже.
Ребята, я предлагаю Вам урок-творчества!
Введение в тему.
От простого к сложному.
Скажите, когда вы дома не убираете за собой, что говорит вам мама?
А как расположены молекулы газа?
Иначе говоря хаотично.
-Хаос понимают как беспорядок, неразбериху, смешение. Понятие возникло от названия в древнегреческой мифологии изначального состояния мира, из которой возникли первые божества. Лишь в раннехристианские времена этому слову стали приписывать значение беспорядка.
-А почему вы сели именно так?
-А расположение молекул твердого тела?
-Порядок в широком смысле слова — гармоничное, ожидаемое, предсказуемое состояние или расположение чего-либо.
-Расположение песка в пустыне беспорядочно, то есть хаотично. А если песчинки привести в порядок, то могут получиться такие замечательные картины. Как это делал Эшер в своих картинах, изображал порядок.
Существование городов на земной поверхности было в хаотичном порядке, пока немецкий географ Мартин Бехайм в 1492 году изобрел модель земли – глобус. Идея задавать положение точки на плоскости зародилась в древности – прежде всего у астрономов. Во II в. древнегреческий астроном Клавдий Птолемей пользовался широтой и долготой в качестве координат.
Координата – это положение точки на плоскости или в пространстве. Термин «координаты» произошел от латинского слова – «упорядоченный»
2. Актуализация опорных знаний. Проверка д/з
1) Проводится устный опрос:
• Как называются оси координат?
• Числа, которые задают точку в системе координат, называются….
• Как называются первая и вторая координаты точки, заданные в координатной плоскости?
• На какие четверти разделена координатная плоскость, назвать знаки абсцисс и ординат в каждой четверти.
• Какой необходимо соблюдать порядок при записи координат точек?
• Если ордината точки А равна 0, то где находится эта точка?
• Если абсцисса точки В равна 0, то где находится эта точка?
Где в практической жизни мы встречаемся с применением координат?
Ответы учеников: определить место в театре, положение фигуры на шахматной доске, на поле игры «Морской бой», карта географическая и т.д.
– Сегодня на уроке мы продолжим изучение данной темы. Открываем тетради, записываем число и тему урока.
– Какие цели мы поставим перед собой на этот урок? Сформулируйте и обоснуйте свои цели. (Дети формулируют цели урока.)
– Работая в группах и выполняя различные задания, вы покажете нам свои знания, умения и навыки, способность применять их в различных ситуациях.
А сейчас давайте узнаем с чьим именем связано прямоугольная система координат?
Математический кроссворд
По горизонтали:
Вспомните компоненты действия деления. Как называется то число, которое делим?
Значение переменной, которое обращает уравнение в верное числовое равенство.
Параллелепипед, в котором все ребра равны.
Вспомните компоненты действия сложения. Как называется число, которое складывают?
Равенство, содержащее неизвестное число, обозначенное буквой.
Результат действия деления.


Ответы:
|
|
| 1 | Д | Е | Л | И | М | О | Е |
| 2 | К | О | Р | Е | Н | Ь |
|
|
|
|
|
|
|
|
| 3 | К | У | Б |
|
|
|
|
|
|
| 4 | С | Л | А | Г | А | Е | М | О | Е |
|
|
|
| 5 | У | Р | А | В | Н | Е | Н | И | Е |
| 6 | Ч | А | С | Т | Н | О | Е |
|
|
|
|
Найдите получившуюся по вертикали фамилию человека, о котором и пойдет речь на сегодняшнем уроке.
Ответ: Декарт
Рене́ Дека́рт (1596 — 1650) — французский математик, философ, физик и физиолог.
Именно он придумал в 1637 году систему координат, которая используется во всем мире и известна каждому школьнику. Ее называют также - Декартова система координат.
Координатный метод описания геометрических объектов положил начало особой ветви математики - аналитической геометрии.
Декарт заложил основы аналитической геометрии, дал понятия переменной величины и функции, ввел многие алгебраические обозначения. Высказал закон сохранения количества движения, дал понятие импульса силы. Автор теории, объясняющей образование и движение небесных тел вихревым движением частиц материи (вихри Декарта). Р. Декарт ввел представление о рефлексе (дуга Декарта).
3- Давайте вместе с Вами испытаем наслаждение творчеством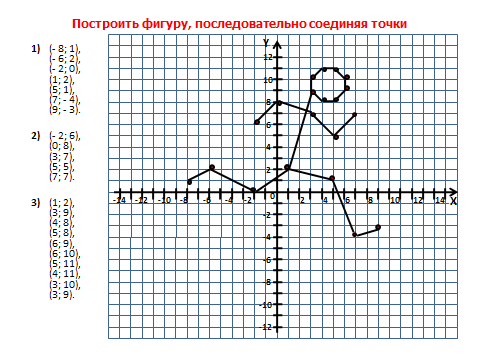
4.Работа в парах
ПРИЛОЖЕНИЕ 1. (работа в группах в парах - взаимопроверка)
| 1 вариант. | . |
| Сколько чисел надо указать, чтобы задать положение точки на координатной плоскости? | две |
| Как называется первое число, задающее положение точки на координатной плоскости? | абсцисса |
| Запишите координату точки К ,если её абсцисса равна 8, а ордината -3. | (8 ,-3) |
| Чему равна ордината точки B(-5 ;-7)? | -7 |
| В какой четверти координатной плоскости находится точкаC(8;--2)? | 4 |
|
2 вариант |
|
| Как называются числа , задающие положение точки на координатной плоскости? | координата |
| Как называется второе число, задающее положение точки на координатной плоскости? | ордината |
| Запишите координаты точки В, если её абсцисса равна -5, а ордината8. | (-5 ,8) |
| Чему равна абсцисса точки D (7;-3) | 7 |
| В какой четверти координатной плоскости находится точка P(-11;-14) | 3 |
Взаимопроверка с готовыми ответами

Работа в группах( по рядам) 1 ряд "БОЛЬШАЯ МЕДВЕДИЦА"
А(-15,0) - В(-10,2) - С(-1,5) - D(-3,0) - Е(6,1) - F(5,-3) - G(-l,-3) – D
2 ряд " ПЕРСЕЙ "
А(-5,-3) - В(-2,-2) - С(0,-1) - D(2,-2) - E(4,-l) - F(5,0) - G(6,2)
H(l,3) - K(1,0) – С
3 ряд "КАССИОПЕЯ "
А(-3,2) - В(-1,0) - С( 1,1) - D(3,-2) - Е(5,0)
довольно яркое созвездие в виде латинской буквы W (см. рисунок). Это и есть Кассиопея.
Творческая работа. Построить фигуру, последовательно соединяя заданные точки на координатной плоскости
Красивые задания на координатной плоскости
Верблюд
(- 9; 6), (- 5; 9), (- 5; 10), (- 4; 10), (- 4; 4), (- 3; 4), (0; 7), (2; 4), (4; 7), (7; 4),
(9; 3), (9; 1), (8; - 1), (8; 1), (7; 1), (7; - 7), (6; - 7), (6; - 2), (4; - 1), (- 5; - 1), (- 5; - 7),
(- 6; - 7), (- 6; 5), (-7;5), (- 8; 4), (-9; 4), (- 9; 6).
2) Глаз: (- 6; 7).
Слоник
1) (2; - 3), (2; - 2), (4; - 2), (4; - 1), (3; 1), (2; 1), (1; 2), (0; 0), (- 3; 2), (- 4; 5), (0; 8),
(2; 7), (6; 7), (8; 8), (10; 6), (10; 2), (7; 0), (6; 2), (6; - 2), (5; - 3), (2; - 3).
2) (4; - 3), (4; - 5), (3; - 9), (0; - 8), (1; - 5), (1; - 4), (0; - 4), (0; - 9), (- 3; - 9), (- 3; - 3), (- 7; - 3), (- 7; - 7), (- 8; - 7), (- 8; - 8), (- 11; - 8), (- 10; - 4), (- 11; - 1), (- 14; - 3),
(- 12; - 1), (- 11;2), (- 8;4), (- 4;5).
3) Глаза: (2; 4), (6; 4).
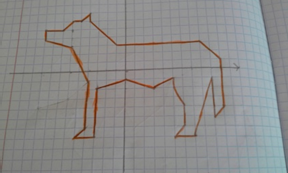
 Волк
Волк
1) (- 9; 5), (- 7; 5), (- 6; 6), (- 5; 6), (- 4; 7), (- 4; 6), (- 1; 3), (8; 3), (10; 1), (10; - 4),(9; - 5), (9; - 1), (7; - 7), (5; - 7), (6; - 6), (6; - 4), (5; - 2), (5; - 1), (3; - 2), (0; - 1),(- 3; - 2), (- 3; - 7), (- 5; - 7), (- 4; - 6), (- 4; - 1), (- 6; 3), (- 9; 4), (- 9; 5).
2) Глаз: (- 6; 5)

Страус
1) (0; 0), (- 1; 1), (- 3; 1), (- 2; 3), (- 3; 3), (- 4; 6), (0; 8), (2; 5), (2; 11), (6; 10), (3; 9), (4; 5), (3; 0), (2; 0), (1; - 7), (3; - 8), (0; - 8), (0; 0).
2) Глаз: (3; 10). Лис
1) (- 8; - 9), (- 6; - 7), (- 3; - 7), (1; 1), (1; 3), (4; 7), (4; 4), (7; 2,5),
(4; 1), (6; - 8), (7; - 8), (7; - 9), (5; - 9), (3; - 3), (1,5; - 6), (3; - 8), (3; - 9), (- 8; - 9).
2) Глаз: (4; 3). 
Гусь
1) (- 3; 9), (- 1; 10), (- 1; 11), (0; 12), (1,5; 11), (1,5; 7), (- 0,5; 4), (- 0,5; 3), (1; 2),
(8; 2), (10; 5), (9; - 1), (7; - 4), (1; - 4), (- 2; 0), (- 2; 4), (0; 7), (0; 9), (- 3; 9).
2) Крыло: (1; 1), (7; 1), (7; - 1), (2; - 3), (1; 1).3) Глаз: (0; 10,5). 
Динозавр
(1;2) (3;4) (7;5) (9;4) (14;0) (20;-6) (10;0) (9;-2) (9;-4) (6;-4) (7;-3) (7;-2) (2;-2)
(2;-4) (-1;-4) (0;-3) (0;0) (-5;4) (-7;4) (-8;5) (-6;7) (-5;7) (1;2) глаз (-6;6).
Лебедь
1) (2; 7), (0; 5), (- 2; 7), (0; 8), (2; 7), (- 4; - 3), (4; 0), (11; - 2), (9; - 2), (11; - 3),
(9; - 3), (5; - 7), (- 4; - 3).
2) Клюв: (- 4; 8), (- 2; 7), (- 4; 6). 
3) Крыло: (1; - 3), (4; - 2), (7; - 3), (4; - 5), (1; - 3).
4) Глаз: (0; 7).
Домашнее задание: построить на бумаге А-4 нарисовать свой рисунок
Рефлексия:
Какое предложение каждый из вас продолжит:
сегодня я узнал…
было интересно… было трудно…
я выполнял задания…
я понял, что…
теперь я могу… я почувствовал, что…
я приобрел…
я научился… у меня получилось …
я смог…
я попробую…
меня удивило Мне тоже было с вами интересно.


 Получите свидетельство
Получите свидетельство Вход
Вход








 Волк
Волк













 Урок математики по теме "Координатная плоскость" (0.61 MB)
Урок математики по теме "Координатная плоскость" (0.61 MB)
 0
0 1242
1242 15
15 Нравится
0
Нравится
0






