Открытый урок по теме: «Нахождение значений тригонометрических выражений» (элективное занятие подготовка к ЕГЭ)
Здравствуйте, ребята!
Здравствуйте все, кто нас видит и слышит, кто с нами на связи.
Наше занятие хотелось бы начать с высказывания французского писателя Анатоля Франса. Он заметил, что…СЛ1
Учиться можно только весело….
Чтобы переваривать знания, надо поглощать их с аппетитом.
Так вот, давайте сегодня на занятии будем следовать этому совету писателя, будем активны, внимательны.
Тема нашего занятия «Нахождение значений тригонометрических выражений». СЛ2
Сегодня мы разберем часть примеров из открытого банка заданий ЕГЭ (это 10-е задание в вариантах по подготовке к егэ) на вычисление тригонометрических выражений. Примеры довольно простые, большинство из них, при определённом навыке, можно решить устно. Поэтому, если вы знаете свойства тригонометрических функций, их значения, формулы тригонометрии, то с решением не будет никаких трудностей.
Цели нашего сегодняшнего занятия: СЛ3
Выработать навыки решения заданий на нахождение значений тригонометрических выражений, выделив общую идею решения
Обеспечить применение этих навыков на практике
СЛ4
| Томас Пейн — Англоамериканский писатель, философ, публицист, прозванный «крёстным отцом США». В 1794 году написал философский труд «Век разума»,где назвал тригонометрию «душой науки»[2].
|
|
|
Сегодня мы рассмотрим выражения, где в ходе решения используются: СЛ5
формулы приведения,
свойства периодичности тригонометрических функций,
свойство чётности нечётности,
формулы – синуса и косинуса двойного аргумента ,
основное тригонометрическое тождество.
Обратите внимание на рекомендации по решению этих задач:
СЛ6
— если в выражении видите, что один угол больше другого в два раза, то смело используйте соответствующую тригонометрическую формулу двойного аргумента;
— если вы видите, что сумма данных углов (или их разность) составляет 90, 180, 270, 360 градусов, то применяйте формулы приведения.
Рассмотрим задачи:
СЛ7
Найдите значение выражения
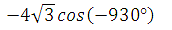
? Что используется в ходе решения задачи?
Свойство четности функции косинуса, то есть
Её периодичность, период равен 2Пn, то есть
И формулу приведения для косинуса:
Ответ: 6
СЛ8
Найдите значение выражения
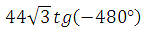
? Что используется в ходе решения задачи?
Свойство нечетности функции тангенса
Её периодичность, период равен 180 градусам (или Пи радиан)
И формулу приведения для тангенса:
Ответ: 132
СЛ9
Найдите значение выражения
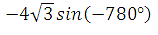
Применяем свойство нечётности синуса,
выделяем период :
Ответ: 6
СЛ10
Найдите значение выражения
Используем формулы приведения:
*Применили формулу тригонометрии:
Ответ: –5
17289. Найдите значение выражения
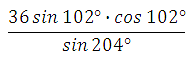
Увидели угол в два раза больше.
Используем формулу синуса двойного аргумента:
Сколько путей решения имеет эта задача?
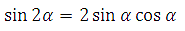
Ответ: 18
63139. Найдите значение выражения
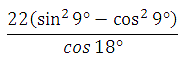
Для решения этого примера достаточно знать какую формулу?
косинуса двойного аргумента:Преобразуем знаменатель:Ответ: –22
63229. Найдите значение выражения
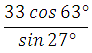
? Какую рекомендацию вы сдесь используете?
Видим, что сумма углов равна 90 град (формула приведения)
В данном случае 63 градуса представляем как разность 900 – 270
Ответ: 33
63763. Найдите значение выражения
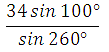
Здесь? (сумма 360 градусов, периодичность синуса)
Представим 1000 как разность 3600 – 2600, применим свойство периодичности нечётности синуса:
Ответ: –34
63819. Найдите значение выражения
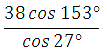
Сумма 180
Используем формулу приведения косинуса.
Представим 1530 как разность 1800 – 270:
Ответ: –38
СЛ11
97369. Найдите значение выражения
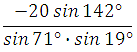
Применяем формулу синуса двойного аргумента в числителе,
и формулу приведения в знаменателе:
Ответ: –40
97967. Найдите значение выражения
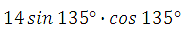
Применяем формулу синуса двойного аргумента:
Ответ: –7
64097. Найдите значение выражения
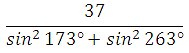
Используем формулы приведения и основное тригонометрическое тождество:
Ответ: 37
63875. Найдите значение выражения
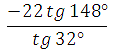
Используем формулу приведения для тангенса.
Представим 1480 как разность 1800 – 320
нечетность тангенса:
Ответ: 22
63929. Найдите значение выражения
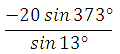
Представим 3730 как сумму 3600 + 130,
используем свойство периодичности:
Ответ: –20
СЛ12
ОТДОХНИТЕ
СЛ13
Решите самостоятельно:
ПРОВЕРЬТЕ ОТВЕТЫ:
СЛ14
СЛ15
Улыбнитесь, помашите ручкой школам, которые нас смотрят
Запишем домашнее задание
СЛ16
И скажем СЛ17
До новых встреч всем участникам этого занятия.
Тест
Найдите значения выражений
1). 24√2cos(-1350)
2) 21√6 tg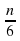 sin
sin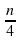
3) 33cos230/sin670
4) 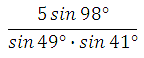
5) 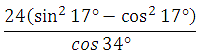
6) 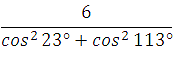
7) 39 tg1120* tg2020
8) 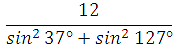
9) √50cos29п/8 - √50sin29п/8
10) 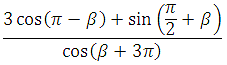
.


 Получите свидетельство
Получите свидетельство Вход
Вход



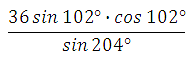
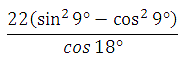
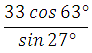
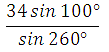
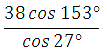
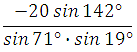
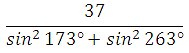
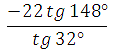
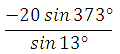
 sin
sin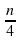
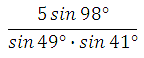
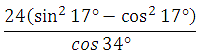
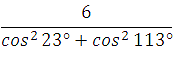
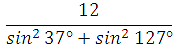
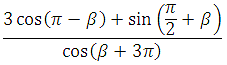









 Урок математики «Нахождение значений тригонометрических выражений» (подготовка к ЕГЭ) (68.28 КB)
Урок математики «Нахождение значений тригонометрических выражений» (подготовка к ЕГЭ) (68.28 КB)
 1
1 856
856 108
108 Нравится
0
Нравится
0



