Нурбаева Дарима Бальчиновна, учитель математики МАОУ СОШ №13 г.Улан-Удэ
Урок-путешествие.
6 класс.
Тема урока: «Пропорции»
Цель: ввести понятие пропорции, ее членов; научить чтению пропорции и составлению пропорций из отношений; закрепить правила деления десятичных дробей, обыкновенных дробей.
Учитель:
Сегодня мы совершим путешествие на планету «Пропорция». В путешествие отправляется весь класс-экипаж ракеты. Следить за путешествием будет Центр управления полетом. Мы побываем в Волшебном саду , на озере «Познания», на водопаде «Закрепления», Музее истории пропорции, во Дворце Смекалки.
1.Операция « Компьютер».
Требуется проверить блок памяти и исправить неполадки
Найди ошибку:
№755
1)240+10=250( г)-раствор
1)10:250=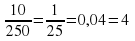
2)250-50=200 (г)- после испарения
3)10:2000=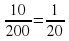 =0,5=50%
=0,5=50%
№756
1)76-12=64 (т)-по плану
2)76:64=1,1875=11,875%
№761(в)
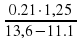 =
=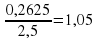
2.Ракета
Экипаж должен путешествовать в ракете. Чтобы в неё попасть, надо преодолеть 4 ступеньки.
Что называют отношением двух чисел?
Что показывает отношение двух чисел?
Как узнать, какую часть число а составляет от числа в?
Как узнать, сколько процентов одно число составляет от другого?
3.Волшебный сад
Поздравляю, вы прилетели на планету «Пропорция» и приземлились в Волшебном саду. Нужно нарядить елку.
Математическая эстафета « Наряди елку».








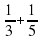
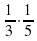
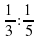
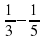
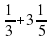
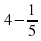
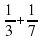
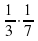
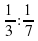
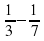
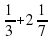
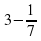
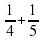





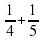

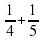
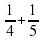
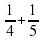
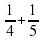
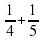
4.Озеро «Познавания»
На озере мы познакомимся с понятием «Пропорция».
Найдите числовые значения двух отношений: 6 : 3 и 10 : 5.
Мы видим, что они равны: 6 : 3 = 2 и 10 : 5 = 2, следовательно, можно записать равенство 6 : 3 = 10 : 5. Такое равенство отношений называют пропорцией.
2. Определение. Пропорцией называется равенство двух отношений. Числа, составляющие пропорцию (6; 3; 10; 5), называются членами пропорции.
3. Пропорцию можно записать с помощью букв: а : в = с : d, или  .
.
4. Эти записи читают: «Отношение а к в равно отношению с к d» или «а так относится к в, как с относится к d».
5. Числа а и d называют крайними членами, а числа в и с – средними членами.
В дальнейшем считают, что все члены пропорции отличны от нуля:
а 0, в 0, с 0, d 0.
6. Чтобы проверить, верно ли составлена пропорция, вычисляют числовое значение каждого отношения, составляющего пропорцию. Если эти отношения равны, то пропорция составлена верно; если не равны, то пропорция составлена неверно.
Примеры: 1) Пропорция 40 : 8 = 65 : 13 составлена верно, так как 40 : 8 = 5 и 65 : 13 = 5.
2) Пропорция 2,7 : 9 = 2 : 5 составлена неверно, так как 2,7 : 9 = 0,3, а 2 : 5 = 0,4.
5. Водопад «Закрепления».
Чтобы благополучно пройти водопад, требуется выполнить следующие задания.
1. Решить устно: а) Прочитайте пропорцию:
1) 18 : 6 = 24 : 8; 2) 30 : 5 = 42 : 7; 3) 36 : 9 = 50 : 10.
б) Назовите крайние и средние члены пропорции.
в) Верно ли составлены пропорции? Проверьте.
2. Составьте, если можно, пропорции из следующих отношений:
а) 20 : 4 и 60 : 12; б) 6,3 : 0,9 и 2,8 : 0,4; в) 0,25 : 5 и 0,3 : 6.
3. Составить три пропорции (учащиеся на доске и в тетрадях приводят свои примеры пропорций).
6. Музей истории планеты.
Благополучно преодолев водопад, мы подошли к Музею истории
Пропорции.
Войдем туда и узнаем много интересного о происхождении пропорции.
Сообщение ученицы.
7. Дворец Смекалки
Конечный и главный пункт нашего путешествия - Дворец Её Величества
Смекалки.
Кирпич весит 2 кг и еще полкирпича. Сколько весит кирпич? (3 кг)
Пара лошадей пробежала 40 км. Сколько километров пробежала каждая лошадь? (40 км)
У семи братьев по одной сестре. Сколько всего детей? (8)
К Айболиту на прием пришли звери. Все, кроме 2, собаки. Все, кроме 2, кошки. Все, кроме 2, зайцы. Сколько животных пришло к Айболиту? (3)
Зайцы пилят бревно. Они сделали 12 распилов. Сколько получилось чурбаков? (13)
Молодцы, ребята! Путешествие окончено. Возвращаемся домой.
1. Вопросы: а) Что такое пропорция?
б) Как называются числа х и у в пропорции х : а = в : у?
в) Как называются числа m и n в пропорции а : m = n : в?
2. Привести свои примеры верных пропорций.
Домашнее задание: выучить из п. 21 (1-ю часть); решить № 776, 778, 781 (а).


 Получите свидетельство
Получите свидетельство Вход
Вход


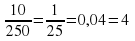
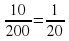 =0,5=50%
=0,5=50%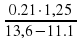 =
=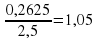








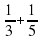
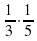
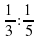
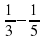
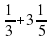









 Урок математики на тему "Пропорция" (43.54 КB)
Урок математики на тему "Пропорция" (43.54 КB)
 0
0 551
551 51
51 Нравится
0
Нравится
0


