Урок геометрии в 9 классе. Тема: «Формулы радиусов вписанной и описанной окружностей.»

Школа-гимназия

имени С.М. Кирова

с. ТЕПЛОКЛЮЧЕНКА

2019-2020 уч.год

Князева Ольга

Владимировна

учитель математики

Урок геометрии

В 9 классе

Тема: « Формулы радиусов вписанной и описанной окружностей. »

ОСНОВОЙ ВЫВОДА ФОРМУЛЫ ДЛИНЫ ОКРУЖНОСТИ ЯВЛЯЕТСЯ ТО, ЧТО РАЗВЁРНУТОМУ УГЛУ СООТВЕТСТВУЕТ ДЛИНА ПОЛУОКРУЖНОСТИ.

ГРАДУСНАЯ МЕРА ЦЕНТРАЛЬНОГО УГЛА

180º

ДЛИНА ДУГИ ОКРУЖНОСТИ, СООТВЕТСТВУЮЩЕЙ УГЛУ

1º

πR

πR

nº

180º

πR · n

180º

• Т.к. градусной мерой дуги окружности является градусная мера соответствующего центрального угла, то длина дуги окружности, соответствующей центральному углу nº, вычисляется по формуле:

l = πR · n

180º

Соотношения между градусной и радианной мерами угла

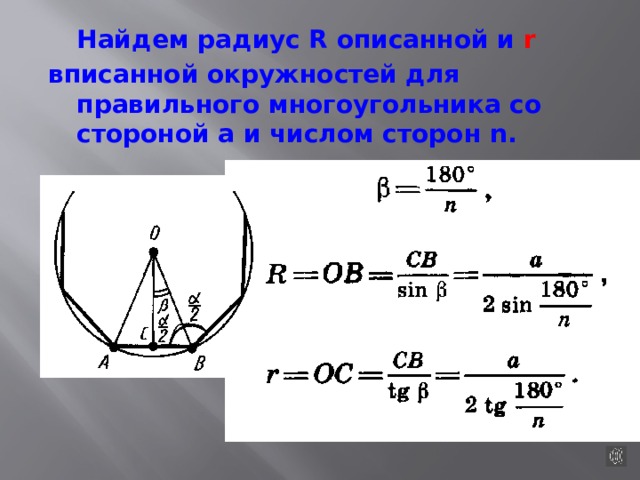
Найдем радиус R описанной и r

вписанной окружностей для правильного многоугольника со стороной а и числом сторон n.

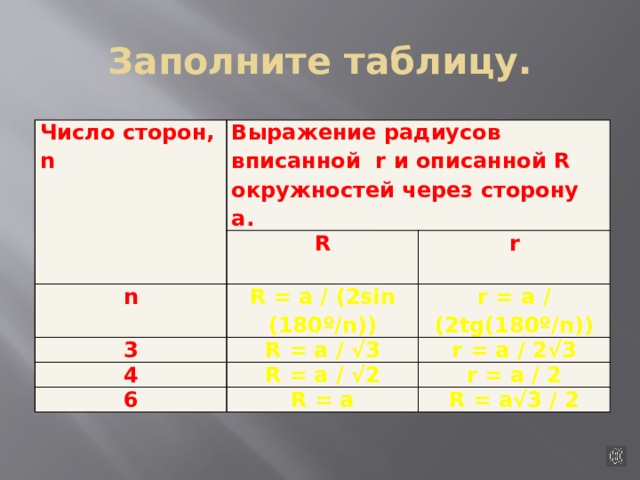
Заполните таблицу.

Число сторон, n

Выражение радиусов вписанной r и описанной R окружностей через сторону а.

R

n

R = a / (2sin (180º/n))

3

r

r = a / (2tg(180º/n))

R = a / √3

4

R = a / √2

r = a / 2√3

6

r = a / 2

R = a

R = a√3 / 2

1. з адача.

Дано: n – число сторон

правильного многоугольника,

a n – сторона.

Выразить R и r через а n и n.

Решение:

Рассмотрим ∆АОВ, АО = ОВ = R, ОD = r, ОD – биссектриса и медиана равнобедренного треугольника.

Задача . Выразить сторону правильного многоугольника через R и r :

при n = 3; а n = 2Rsin 60° =

а 3 = 2rtg 60° = 2

Самостоятельно получите формулы:

•   при n = 4;
• при n = 6.

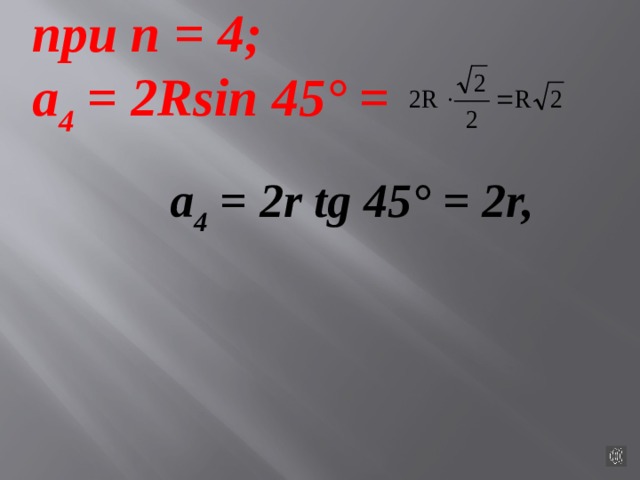
при n = 4;

а 4 = 2Rsin 45° =

а 4 = 2r tg 45° = 2r,

при n = 6

а 6 = 2Rsin 30° = R,

а 6 = 2rtg 30° =

Изображение вписанных и описанных окружностей.

Рассмотрим способы построения некоторых правильных многоугольников с помощью циркуля и линейки. Постройте справа чертёж, а слева запишите описание построения.

1. Шестиугольник.

• Строим окружность.
• Выбираем произвольную точку А1.Из точки А1 радиусом окружности делаем засечки.
• Соединяем попарно полученные точки и получаем правильный шестиугольник.

2. Треугольник.

  1. Построение аналогичное шестиугольнику.

2. Но из полученных шести точек на окружности, соединять надо через одну и получаем правильный треугольник.

3. Квадрат.

1. Строим окружность.

2. Проводим через центр окружности два перпендикулярных диаметра.

3. Соединяем полученные точки на окружности и получаем квадрат.

4. Построение из n – угольников 2n – угольников.

• Строим окружность.
• Строим квадрат.
• К сторонам квадрата проводим диаметрами серединные перпендикуляры.
• Полученные точки пересечения окружности и серединных перпендикуляров и вершины квадрата соединяем попарно.
• Получаем восьмиугольник.

Дома:

№ 43(1,4),44,46

ПОВТОРЕНИЕ

• ЧТО ТАКОЕ ПЛОСКИЙ УГОЛ?
• ЧТО ТАКОЕ ГРАДУСНАЯ МЕРА УГЛА?
• ЧЕМУ РАВНА ГРАДУСНАЯ МЕРА ДВУХ ДОПОЛНИТЕЛЬНЫХ УГЛОВ?
• КАКОЙ УГОЛНАЗЫВАЕТСЯ ЦЕНТРАЛЬНЫМ?

Сидите дома и не болейте!