Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа №18
имени Виталия Яковлевича Алексеева
| РАССМОТРЕНО На заседании кафедры _________________________ Протокол №______от ________ ____________/______________/ | СОГЛАСОВАНО Зам. директора по_____ ___________/___________/ «___»____________2018 | УТВЕРЖДАЮ Директор МБОУ СОШ № 18 имени В.Я. Алексеева __________/ / «___»_________________2018 |
|
|
|
|
Рабочая программа элективного курса
«Удивительный мир квадратных уравнений»
на 2018 - 2019 учебный год
класс 9А
учитель: Гусева Светлана Геннадьевна
г. Сургут
Пояснительная записка.
Рабочая программа элективного курса в 9А классе составлена на основе рабочей программы по алгебре и геометрии основного общего образования и учебников Алгебра 9 класс: Ю.Н. Макарычев, Н. Г. Миндюк, К.И. Нешков, С.Б. Суворова; под. ред. С.А. Теляковского – М.: Просвещение, 2014г., Геометрия: 7 – 9 кл. / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. М.: Просвещение, 2017г.
Элективный курс «Удивительный мир квадратных уравнений» предназначен для учащихся 9-х классов, интересующихся математикой. Данный курс можно изучать целостно, как отдельный курс, или использовать его элементы как на уроках математики 9 классе, так и на занятиях кружков и факультативов. Предлагаемый курс более полно освещает намеченные в школьном курсе математики вопросы, связанные с историей, решением различных видов квадратных уравнений, а также уравнений, сводящихся к ним.
Стоит отметить, что навыки решения различных видов квадратных уравнений необходимы каждому ученику, желающему успешно подготовиться к итоговой аттестации по математике, и будет хорошим подспорьем для подготовки к математическим олимпиадам и дальнейшему обучению в профильном математическом классе.
Познавательный материал курса позволит школьникам не только выработать умения и навыки решения квадратных уравнений, но и поможет им систематизировать, расширить и укрепить знания, связанные с квадратными уравнениями, подготовиться к дальнейшему изучению тем, использующих навыки решения квадратных уравнений.
Наряду с обеспечением прочного и сознательного овладения учащимися системой математических знаний и умений данный курс предусматривает формирование устойчивого интереса к предмету, выявление и развитие математических и исследовательских способностей, ориентация на профессии, связанные с математикой, выбору профиля дальнейшего обучения.
Учебный процесс данного курса предполагает использование типового школьного оборудования кабинета математики.
Общая характеристика курса
Актуальность курса состоит в том, что он направлен на расширение знаний учащихся по математике, развитие их теоретического мышления и логической культуры.
Новизна данного курса заключается в том, что программа включает новые для учащихся задачи, не содержащиеся в базовом курсе. Предлагаемый курс содержит задачи по разделам, которые обеспечат более осознанное восприятие учебного материала. Творческие задания позволяют решать поставленные задачи и вызвать интерес у обучаемых. Включенные в программу задания позволяют повышать образовательный уровень всех учащихся, так как каждый сможет работать в зоне своего ближайшего развития.
Отличительные особенности данного курса от уже существующих в том, что этот курс подразумевает доступность предлагаемого материала для учащихся, планомерное развитие их интереса к предмету. Сложность задач нарастает постепенно. Приступая к решению более сложных задач, рассматриваются вначале простые, входящие как составная часть в решение трудных. Развитию интереса способствуют математические игры, викторины, проблемные задания и т.д.
Программа ориентирована на учащихся 9 классов, которым интересна как сама математика так и процесс познания нового.
Занятия рассчитаны на 1 час в неделю, в общей сложности – 35 ч в учебный год. Преподавание курса строится как углубленное изучение вопросов, предусмотренных программой основного курса. Углубление реализуется на базе обучения методам и приемам решения математических задач, требующих высокой логической и операционной культуры, развивающих научно-теоретическое и алгоритмическое мышление учащихся. Занятия дают возможность шире и глубже изучать программный материал, задачи повышенной трудности, больше рассматривать теоретический материал и работать над ликвидацией пробелов знаний учащихся, и внедрять принцип опережения.
Цель: развитие у ученика умения сделать ответственный выбор профиля и способа дальнейшего обучения.
Задачи:
1) создание у учащихся положительной мотивации обучения на профильном курсе;
2) помощь ученикам в оценке своего потенциала с точки зрения образовательной перспективы;
3) помощь ученикам утвердится в сделанном ими выборе направления дальнейшего обучения, связанного с математикой, или отказаться от него;
4) восполнение содержательных пробелов основного курса, придающих ему необходимую целостность;
5) освоение нестандартных приемов решения квадратных уравнений и уравнений к ним сводящихся.
Основные формы организации учебных занятий: лекция, диалог, объяснение, практикум, различные формы групповой и индивидуальной работы.
Количество часов и объем изучаемого материала позволяют принять темп продвижения по курсу, который соответствует возрасту учащихся.
Отработка и закрепление основных умений и навыков осуществляется на большом числе доступных учащимися упражнений. В то же время это не означает монотонной и скучной деятельности, так как курс наполнен заданиями, разнообразными по форме и содержанию.
Формирование важнейших умений и навыков происходит на фоне развития умственной деятельности - дети учатся анализировать конкретные ситуации, замечать существенное, подмечать общее и делать обобщения, переносить известные приемы в нестандартные ситуации, находить пути их решения.
Условием, позволяющим правильно построить учебный процесс, является то, что изучение каждой темы начинается с проведения установочных занятий, выделяется главное и, исходя из этого, дифференцируется материал: выделяются те задачи, на которых происходит отработка ЗУН, и, те, которые служат развитию, побуждению интереса и др., и в соответствии с этим они не дублируются.
Материал курса доступен для обучения, способствует развитию логического мышления учащихся, повышению интеллектуального и творческого уровня, математической культуре. В процессе работы динамика интереса к элективному курсу будет фиксироваться с помощью диагностики на первом и последнем занятии. На всех этапах занятий предусматривается активный диалог с учащимися. Доля самостоятельности учеников при изучении курса достаточно велика, они могут проявлять активность, реализовывать свой творческий потенциал.
Большинство задач данного курса – это задания, в которых предлагается самостоятельно установить алгоритм решения, т.е. провести небольшое самостоятельное математическое исследование, что существенно способствует развитию логического мышления.
Итоговой формой контроля, подводящей изучение курса к логическому завершению, является проведение круглого стола.
Для учащихся, которые пока не проявляют заметного интереса к математике, эти занятия могут стать толчком к увлечению предметом и вызвать желание узнать больше. Программа может быть эффективно использована в 9-ом классе с любой степенью подготовленности, способствует развитию познавательных интересов учащихся, предоставляет возможность подготовиться к сознательному выбору математического профиля обучения или отказ от него.
Содержание курса.
Программа курса рассчитана на 35 часов и предполагает знакомство с теорией и практикой рассматриваемых вопросов. Предлагаемые задачи различны по уровню сложности: от простых упражнений на применение изученных формул до достаточно трудных заданий. В основном занятия состоят из 2-х частей: задачи, решаемые с учителем, и задачи, для самостоятельного (или домашнего) решения.
Тема 1. Квадратные уравнения.(7 часов)
Неполные квадратные уравнения.(2 часа)
Решение уравнений вида: а) с = 0, тогда уравнение имеет вид ax2+bx=0
б) b=0, тогда уравнение примет вид ax2+c=0
в) b = c = 0, тогда уравнение принимает вид ax2=0;
Полные квадратные уравнения.(2 часа)
Решение уравнений вида уравнение вида ![]() , где
, где ![]() Нахождение дискриминанта. При D 0, то корни действительные и различные
Нахождение дискриминанта. При D 0, то корни действительные и различные ![]() ;
;
при D = 0 корни совпадают (говорят, что уравнение имеет корень кратности два),
при D
Теорема Виета.(3 часа)
Решение уравнений применяя формулу Виета ![]() ,
,
тогда 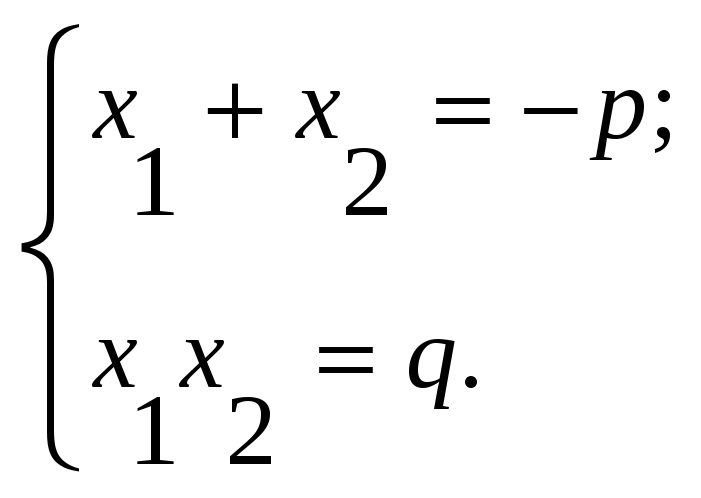
Тема 2. Нестандартные способы решения квадратных уравнений.(6 часов)
Частные случаи нахождения корней полного квадратного уравнения.(2 часа)
В некоторых случаях можно решить квадратные уравнения, не считая его дискриминант.
1) Если ![]() , то
, то ![]()
2) Если ![]() , то
, то ![]()
3) Если ![]() , то есть уравнение имеет вид
, то есть уравнение имеет вид ![]() , то
, то
![]()
4) Если ![]() , то есть уравнение имеет вид
, то есть уравнение имеет вид ![]() , то
, то ![]()
Решение квадратных уравнений методами геометрической арифметики.(2 часа)
Познакомить учащихся с идеями геометрической арифметики и показать учащимся возможность решения квадратного уравнения геометрическим способом;
Решение квадратных уравнений с применением циркуля и линейки.(2 часа)
Научить решать квадратные уравнения с применением циркуля и линейки;
Тема 3. Решение уравнений сводящихся к квадратным.(22 часа)
Квадратные уравнения с модулем.(2 часа)
Решение квадратного уравнения с помощью раскрытия модуля.
Решение уравнений методом разложения на множители.(3 часа)
Показать учащимся возможность решения уравнений методом разложения на множители;
Развивать умение учащихся раскладывать многочлены на множители;
Решение уравнений методом введения новой переменной.(3 часа)
Решение биквадратных уравнений, т.е. уравнения вида
![]() которые сводятся к квадратным заменой y=x2. Введения новой переменной.
которые сводятся к квадратным заменой y=x2. Введения новой переменной.
Решение иррациональных уравнений.(3 часа)
Различные виды иррациональных уравнений.
Уравнения вида
![]() сводится к квадратному заменой переменной
сводится к квадратному заменой переменной ![]()
Рассмотрим уравнение
![]()
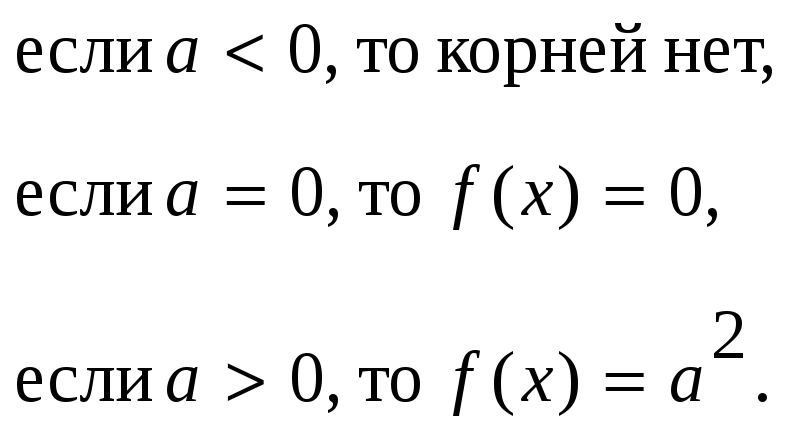
Решение возвратных уравнений.(4 часа)
Возвратным называется уравнение вида ![]()
В этом уравнении коэффициенты членов, равноотстоящих от начала до конца, одинаковы. Возвратное уравнение не имеет корня, равного нулю. Если же оно имеет корень x1, то оно имеет корень ![]()
Решение симметричных уравнений.(5 часов)
Познакомить учащихся с понятием симметричных уравнений и методами их решения.
Тематическое планирование
| № п/п | Раздел | Общее количество часов |
| 1 | Квадратные уравнения. | 7 |
| 2 | Нестандартные способы решения квадратных уравнений. | 6 |
| 3 | Решение уравнений сводящихся к квадратным. | 22 |
|
| Итог | 35 |
Календарно - тематическое планирование.
| № п/п | Тема занятия | Кол-во часов | Дата план | Дата факт | Основные вопросы, рассматриваемые на занятии | Характеристика основных УУД |
|
| 1. Квадратные уравнения. | 7 |
|
|
|
|
| 1-2 | Неполные квадратные уравнения. | 2 | 06.09 13.09 |
| Квадратные уравнения. Неполные квадратные уравнения. Дискриминант | Вспоминают алгоритм решения неполных квадратных уравнений. Развивают логику и внимательность. |
| 3-4 | Полные квадратные уравнения. | 2 | 20.09 27.09 |
| Полные квадратные уравнения. Дискриминант | Решают квадратные уравнения применяя дискриминант |
| 5-6 | Теорема Виета. | 2 | 04.10 11.10 |
| Теорема Виета. Корни уравнения. Коэффициенты. | Решают квадратные уравнения применяя теорему Виета. Развивают свою смекалку, логику и внимательность. |
| 7 | Обобщающее занятие-игра. | 1 | 18.10 |
|
|
|
|
| 2. Нестандартные способы решения квадратных уравнений. | 6 |
|
|
|
|
| 8-9 | Частные случаи нахождения корней полного квадратного уравнения. | 2 | 25.10 01.11 |
| Полные квадратные уравнения. Дискриминант. Корни уравнения | Решают квадратные уравнения применяя частные случаи |
| 10-11 | Решение квадратных уравнений методами геометрической арифметики. | 2 | 15.11 22.11 |
| Геометрические построения. Квадратный корень | Решают квадратные уравнения применяя геометрическую арифметику. Развивают логику и внимательность. |
| 12-13 | Решение квадратных уравнений с применением циркуля и линейки. | 2 | 29.11 06.12 |
| Окружность, круг, радиус, диаметр | Выполняют решение квадратных уравнений с помощью циркуля и линейки. Развивают свою смекалку, логику и внимательность. |
|
| 3. Решение уравнений сводящихся к квадратным. | 22 |
|
|
|
|
| 14-15 | Квадратные уравнения с модулем. | 2 | 13.12 20.12 |
| Модуль числа. Раскрытие скобок. Квадратные уравнения | Раскрытие модуля при решении квадратных уравнений. Развивают логику и внимательность. |
| 16-18 | Решение уравнений методом разложения на множители. | 3 | 10.01 17.01 24.01 |
| Множитель. Квадратные уравнения | Разложение на множители квадратных уравнений |
| 19-21 | Решение уравнений методом введения новой переменной. | 3 | 31.01 07.02 14.02 |
| Переменная. Квадратные уравнения | Введение новой переменной при решении квадратных уравнений. Развивают свою смекалку, логику и внимательность. |
| 22-24 | Решение уравнений методом введения новой переменной. | 3 | 21.02 28.02 07.03 |
| Переменная. Квадратные уравнения. Дискриминант | Введение новой переменной при решении квадратных уравнений |
| 25-27 | Решение иррациональных уравнений. | 3 | 14.03 21.03 04.04 |
| Иррациональное уравнение. Квадратные корни. Дискриминант | Решение иррациональных уравнений. Развивают свою смекалку, логику и внимательность. |
| 28 | Решение возвратных уравнений. | 1 | 11.04 |
| Коэффициенты. Степени. Уравнения | Решение возвратных уравнений. |
| 29-31 | Решение возвратных уравнений. | 3 | 18.04 25.04 02.05 |
| Коэффициенты. Степени. Уравнения | Решение возвратных уравнений. Развивают свою смекалку, логику и внимательность. |
| 32-33 | Решение симметричных уравнений. | 2 | 08.05 16.05 |
| Симметрия. Симметричные уравнения | Решение симметричных уравнений. Развивают логику и внимательность. |
| 34 | Проверочная работа. | 1 | 23.05 |
|
| Зачет. |
| 35 | Итоговое занятие. | 1 | 30.05 |
|
| Дискуссия. Обсуждение различных способов решения уравнений. Диагностика. |
Результаты освоения программы
В результате изучения темы «Квадратные уравнения» курса учащийся может:
усвоить основные приемы решения различных видов квадратных уравнений;
научиться устно решать простые квадратные уравнения, используя теорему Виета.
В результате изучения темы «Нестандартные способы решения квадратных уравнений» курса учащийся может:
научиться устно решать простые квадратные уравнения, используя зависимости между коэффициентами квадратного уравнения;
получить представление о решении квадратных уравнений методами геометрической арифметики и с использованием циркуля и линейки;
В результате изучения темы «Решение уравнений сводящихся к квадратным» курса учащийся может:
научиться применять различные методы для сведения уравнений к квадратным;
научиться решать основные типы квадратных уравнений с модулем, иррациональных уравнений, возвратных и симметричных уравнений.
Итоговое занятие – заседание «Круглого стола» на тему: «Самое красивое решение. За и против» предполагает дискуссию о различных способах решения предложенных учащимся уравнений, т.к. каждое из них может быть решено несколькими способами или комбинацией различных методов. Такая форма занятия дает возможность для индивидуальной и коллективной исследовательской деятельности.
Ресурсное обеспечение
УМК для учителя.
1. Алгебра: Учеб. для 9 кл. общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк и др.; под ред. С.А. Теляковского. М.: Просвещение, 2014.
2.Геометрия 7 -9. Учебник для общеобразовательных учреждений. Авторы: Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Л. С. Киселева, Э. Г.Позняк— М.: Просвещение, 2017.
3. Алгебра. 9 класс. Итоговая аттестация – 2010 / Под ред. Ф.Ф. Лысенко. – Ростов-на-Дону: Легион, 2017. – 256 с.
5. Галицкий Л.М. Сборник задач по алгебре для 8-9 классов / Л.М. Галицкий, А.М. Гольдман, Л.И. Звавич. – Москва: Просвещение, 1992. – 271 с.
6. Неброева К.Н. Элективные курсы в предпрофильной подготовке / Сост. К.Н. Неброева – Смоленск, 2012. – 40 с.
7. Печурин Л.Ф. За страницами учебника алгебры / Л.Ф. Печурин. – Москва: Просвещение, 1990. – 224 с.
8. Пресман А.С. Решение квадратных уравнений с помощью циркуля и линейки. // Квант. –1972. – № 4.
9. Сборник задач по математике для поступающих в ВУЗы / Под ред. М.И. Сканави. – Москва: ООО «Издательский дом «Оникс 21 век», 2014. – 608 с.
10. Система тренировочных задач и упражнений по математике. / Под ред. А.Я. Симонова. – Москва: Просвещение, 2012. – 208 с.
11. Студенецкая В.Н. Математика. 8-9 классы: сборник элективных курсов / В.Н. Студенецкая, Л.С. Сагателова. – Волгоград: Учитель, 2015. – 205 с.
УМК для учащихся.
1. Алгебра: Учеб. для 9 кл. общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк и др.; под ред. С.А. Теляковского. М.: Просвещение, 2014.
2.Геометрия 7 -9. Учебник для общеобразовательных учреждений. Авторы: Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Л. С. Киселева, Э. Г.Позняк— М.: Просвещение, 2017.
3. Алгебра. Сборник заданий для подготовки к итоговой аттестации в 9 классе / Под ред. Л.В. Кузнецовой. – Москва: Просвещение, 2015. – 191 с.
4. Алгебра. 9 класс. Итоговая аттестация – 2013/ Под ред. Ф.Ф. Лысенко. – Ростов-на-Дону: Легион, 2017. – 256 с.
5. Печурин Л.Ф. За страницами учебника алгебры / Л.Ф. Печурин. – Москва:
Просвещение, 1990. – 224 с.
6. Энциклопедический словарь юного математика / Под ред. А.П. Савина. – Москва: Педагогика, 1989. – 352 с.
Перечень Интернет ресурсов, цифровых образовательных ресурсов и других
электронных информационных источников:
1. www.etudes.ru. Математические этюды. На сайте представлены этюды, выполненные с использованием современной компьютерной 3D-графики, увлекательно и интересно рассказывающие о математике и ее приложениях.
2. www.problems.ru. База данных задач по всем темам школьной математики. Задачи разбиты по рубрикам и степени сложности. Ко всем задачам приведены решения.
3. www.golovolomka.hobby.ru. Головоломки для умных людей. На сайте можно найти много задач (логических, на взвешивания и др.), вариации на тему кубика Рубика, электронные версии книг Р. Смаллиана, М. Гарднера, Л. Кэрролла, ведения занятий, приемах работы на уроках.
8

 Получите свидетельство
Получите свидетельство Вход
Вход












 Удивительный мир квадратных уравнений (167 KB)
Удивительный мир квадратных уравнений (167 KB)
 0
0 289
289 8
8 Нравится
0
Нравится
0


