Получите свидетельство
Вход
O’zbekiston Respublikasi Xalq
Ta’limi Vazirligi
Namangan viloyati xalq ta’limi boshqarmasi
Namangan tumani XTB ga qarashli 11-sonli umumiy o’rta ta’lim maktabi
MATEMATIKA FANI O’QITUVCHISI EGAMBERDIYEVA NARGIZANING
10-sinf Geometriya fanidan
“UCH PERPENDIKULYAR HAQIDAGI TEOREMA” MAVZUSIDA
Yozgan bir soatlik
Namangan tuman
DARSNING TEXNOLIGK XAIRTASI
| Mavzu: Tayanch so’zlar: | Uch perpendikulyar haqidagi teorema Tekilik, perpendikulyar,og’ma,uch perpendikulyar,uch perpendikulyar haqidagi teorema |
| Mavzuning qisqacha ta’rifi: | Ushbu mavzu orqali o’quvchilarni darslik va dasturlar hamda undan tashqari adabiyotlar, internet ma’lumotlari asosida uch perpendikulyar teoremasi haqida bilim, ko’nikma va malakalar hosil qilish. |
| O’quv jarayonini amalga oshirish texnologiyasi: Shakl: Uslub: Vositalar: | amaliy bajarish Hamkorlikda o’qitish. Darslik, ko’rgazmali qurollar, proyektor |
| Dars (amaliyot)ining maqsad va vazifalari | |
| Maqsadlar: Ta’limiy: Tarbiyaviy:
Rivojlantiruvchi: | O’quvchilarga uch perpendikulyar teoremasi haqidagi bilimlar berish. O’quvchilarga geometrik tushunchalar orqali estetik tarbiya berish o’quvchilarni ziyraklik, topqirlik va zukkolikka o’rgatish. O’quvchilarni fanga bo’lgan qiziqishlarini orttirish. |
| Kutilayotgan natijalar | |
| Dars(amaliyot)yakunida o’quvchi biladi(bilim): | Uch perpendikulyar haqidagi teoremani qo’llagan xolda masalalar yecha oladi.
|
| Dars (amaliyot) yakunida o’quvchi tushunadi (ko’nikma): | O’quvchilarga uch perpendikulyar haqidagi teoremani mohiyatini o’rgatish. |
| Dars (Amaliyot)yakunida o’quvchi bajara oladi (malaka) | Har hil misol va masalalar yechish jarayonida uch perpendikulyar teoremasini qo’llay olish. |
Darsning bajarilish bosqichlari
| Bosqichlar | Bajariladigan ish mazmuni | uslub | Vaqt (min) |
| 1- bosqich: Tashkiliy qism | Psixologik muhit yaratish. O’quvchilarni darsga tayyorlash | Savol -javob muloqot | 2 |
| 2-bosqich: (Reflektsiya) Ehtiyojlarni aniqlash | O’tgan mavzu yuzasidan savol javob o’tkazish orqali tushuncha bilim, ko’nikma, malakalarni mustahkamlash | Aqliy hujum | 6 |
| 3-bosqich: Yangi mavzu bayoni | Reja Perpendikulyar va og’ma Uch perpendikulyar haqidagi teorema Masalalar ishlash | Mavzuni o’quvchilar daftariga qayd ettirib borish | 15
|
| 4-bosqich: Mustahkamlash: | Uch perpendikulyar teoremasini masalalar yechish jarayonida qo’llay olish | Guruhlarga bo’lib ishlash | 17 |
| 5-bosqich: baholash
| Darsta faol ishtirok etgan o’quvchilarni rag’batlantirish. O’quvchilarga tushunmaganlarini tushuntirish | Savol javob tushuntirish ishlari | 3 |
| 6-bosqich: Uyga vazifa
| Masala | Tushunitirsh ishlari | 2 |
Darsning borishi
1.Tashkiliy qism: Salomlashish
O’quvchilar- Assalomu alaykum,aziz ustoz muallim,
Bizlar shaymiz saboqqa, siz bizga bering ta’lim.
O’qituvchi- Va alaykum assalom aziz o’quvchilarim,
Kuch bo’lsin sizga hamroh,olingizlar ko’p ilm.
Navbatchi shaymi,ma’lumot bersin endi
Navbatchi bugungi kun,yo’qlama ma’lumotini beradi.
Kun yangiliklari haqida ma’lumotlar eshitiladi. So’ng sinf uch guruhga ajratiladi.O’quvchilar birin –ketin 1,2,3 sonlarini aytib chiqadilar. 1ni aytganlar 1-guruh,2 deganlar 2-guruh va 3ni aytgan o’quvchilar 3-guruhlarga bo’linadilar. 1-guruh “Tekislik”, 2-guruh “Perpendikulyar” va 3-guruh “Og’ma” atamalari orqali nomlanadilar.
Har bir guruhlarga o’tilgan mavzularni takrorlash uchun tarqatmalar beriladi. Har bir tarqatmada uchtadan savol bor bo’lib,o’quvchilar maslahatlashgan holda javob beradilar. Tarqatmalar savollari:
Javoblar tinglanadi.Bir guruh javobini boshqa guruh to’ldirsa o’sha guruh qo’shimcha rag’batlantirib boriladi.
Yangi mavzu bayoni:
M
tekislik
avzuni bayon qilishdan oldin guruhlarga bo’sh qog’ozlar beriladi va ulardan o’z guruhlari nomini kundalik hayotdagi o’rni va rolini tavsiflab berish so’raladi. Ko’p ma’lumot bergan guruh rag’batlantiriladi.
perpendikulyar
og’ma
Uch Perpendikularlar haqidagi teorema
Teorema: Agar tekilikka tushirilgan og’maning asosidan o’tuvchi to’g’ri chiziq og’maning proyeksiyasiga perpendikulyar bo’lsa,u holda u og’maning o’ziga ham perpendiular bo’ladi.
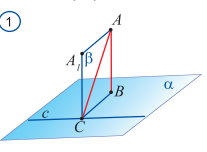
Isbot: Aytaylik, AB kesma tekislikka tushirilganperpendikular,AC kesmaesa og’ma bo’lsin. C to’g’ri chiziq teislikda yotuvchi,C nuqtadan o’tuvchi va og’maproyeksiyasiga perpendikular bo’lgan to’g’ri chiziq bo’lsin(1-rasm).AB ga parallelA1C to’g’ri chiziqni o’tkazamiz. Bu to’g’ri chiziq tekislikkaperpendikular bo’ladi.
AB va AC to’g’ri chiziqlar orqali tekilikni o’tkazamiz. C to’kgri chiziq CA1 to’g’ri chiziqqa perpendikular bo’ladi. U shartga ko’ra , CB to’g’ri chiziqqa ham perpendikular bo’ladi.
Demak, c to’g’ri chiziq tekislikda yotgan AC og’maga ham perpendikularbo’ladi
Mazkur teoremada uchta perpendikular haqida gap borayotgani uchun u “Uch perpendikular haqidagi teorema” nomini olgan.Bu teotemaga teskari bo’lgan teorema ham o’rinli bo’ladi.
Teorema: Agar tekislikka tushirilgan og’maning asosidan o’tuvchi to’gri chiziqogmaga perpendikular bo’lsa, u holda u og’maning proyeksiyasiga ham perpendikular bo’ladi.
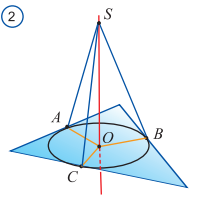
1-masala: Uchburchakka ichki chizilgan aylana markazidan uchburchak tekisligiga perpendikular to’g’ri chiziq o’tkazilgan.Bu to’g’ri chiziqning ixtiyoriy nuqtasi uchburchak tomonlaridan baravar uzoqlikda yotishini isbotlang.
Isbot. Aytaylik,A,B,C-uchburchak tomonlarining aylana bilan kesishish nuqtalari, o-aylana markazi, S esa perpendikulardagi ixtiyoriy nuqta bo’lsin.OA uchburchak tomoniga perpendikular bo’lgani uchun ,uch perpendikularlar haqidagi teoremaga ko’ra, OA ham bu tomonga perpendikular bo’ladi. Unda SOA to’g’ri burchakli uchburchak bo’ladi. Bu uchburchakda pifagor teoremasiga ko’ra, Sa=
Bu yerda r-aylana radiusi.
Xuddi shunga o’xshash, SBO to’g’ri burchakliuchburchakdan SB=
vaSCO to’gri burchakli uchburchakdan esa SC= ekanligini topamiz.
Demak, SA=SB=SC.
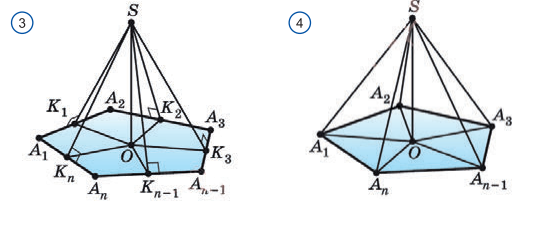
Yuqorida keltirilgan 3-4- rasmlar asosida 1-masalaga o’xshash va ixtiyoriy ko’pburcha uchun umumiyroq hollarni mustaqil isbotlash uchun keltiramiz.
Уч перпендикуляр хакидаги теорема (211.68 KB)
0
350
4
Нравится
0
