Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №2 им. А.И.Герцена г. Клинцы Брянской области
Урок по теме
«Цилиндр».
Подготовила учитель математики
Гетун Т.А.
г. Клинцы 2018 г.
Тип урока: урок объяснения нового материала
Цели урока:
Разобрать определение цилиндра и связанных с ним понятий (образующие, основание, радиус, высота, ось); рассмотреть основные виды сечений цилиндра;
Развитие наблюдательности, умений сравнивать, обобщать, классифицировать объекты по какому-либо признаку; развивать математическую речь;
Воспитание аккуратности, положительных мотивов к учёбе, добросовестного отношения к труду.
Оборудование:
- компьютер
- модели тел вращения
- шаблоны эллипсов.
Ход урока
Организационный момент.
Приветствие, проверка готовности рабочего места к уроку.
Актуализация знаний.
Сообщение темы и целей урока.
Изучение нового материала.
Существуют следующие виды тел вращения: цилиндр, конус, шар. Вы встречались с этими телами в повседневной жизни, на уроках черчения и технологии. Сегодня мы остановимся на цилиндре. Цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг его стороны как оси. В переводе с греческого слово цилиндр валик, каток.
Работа с компьютером.
Слайд №1

Работа с моделями тел вращения.
По модели цилиндра дать его определение.
Слайд №2. Определение цилиндра.

Используя шаблоны эллипсов выполните в тетради рисунок.
Слайд №3.

Назовите образующие. Запишите А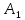 ; В
; В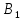 – образующие цилиндра. Образующие у цилиндра параллельны и равны.
– образующие цилиндра. Образующие у цилиндра параллельны и равны.
А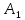 //В
//В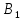 ; А
; А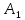 =В
=В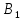 .
.
Постройте ещё одну образующую, обозначьте её. Сколько образующих можно построить?
Слайд №4. Элементы цилиндра.

Назовите радиус цилиндра, высоту цилиндра, ось цилиндра. Запишите: АО; ВО; 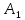 О;
О; 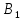 О – радиусы цилиндра; отрезок О
О – радиусы цилиндра; отрезок О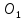 – высота цилиндра; прямая О
– высота цилиндра; прямая О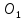 – ось цилиндра.
– ось цилиндра.
Слайд №5. Виды цилиндров.
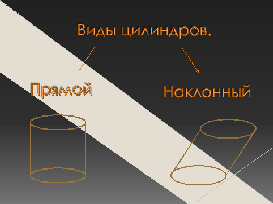
Цилиндр называется прямым, если его образующие перпендикулярны основаниям. В дальнейшем мы будем рассматривать только прямой цилиндр и для краткости называть его просто цилиндром.
У прямого цилиндра образующая равна высоте.
Слайд №6. Площадь поверхности цилиндра.
Как вы думаете, из чего состоит поверхность цилиндра?
Поверхность цилиндра состоит из оснований и боковой поверхности.
Как найти Sполн.?
Sполн=Sбок+2Sосн
Боковая поверхность составлена из образующих и представляет собой прямоугольник. Длина прямоугольника – это длина окружности, а ширина – это высота. Значит, получим формулу Sбок= 2πRH. Sосн=πR².

Как найти Sполн, если известен диаметр основания? Запишите формулы: Sбок=πDH
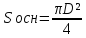
Перейдём к рассмотрению сечений цилиндра плоскостями.
Слайд №7. Сечение цилиндра плоскостями.

Сечение плоскостью, параллельной оси цилиндра. Выполняем рисунок. Какой фигурой является это сечение? Сечение – прямоугольник, сторонами которого являются две параллельные хорды и две образующие цилиндра.
Осевое сечение – сечение плоскостью, проходящей через ось цилиндра. Выполняем рисунок. Сечение – прямоугольник или квадрат.
Сечение плоскостью, параллельной основанию. Выполняем рисунок. Сечение – круг.
Слайд №8. Рассмотрение аналогии с многогранниками.

Цилиндр имеет сходство с прямой призмой.
Закрепление изученного материала. Решение задач.
Слайд №9.

Что известно по условию задачи? Какое сечение построено? Выполняем рисунок и наносим на него данные.
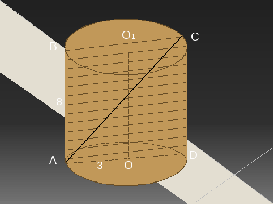
Решение:
Из прямоугольного ∆ACD по теореме Пифагора: АС=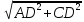
AD=2АО, AD=2×3=6(см); АС=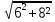 =
=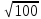 =10(см)
=10(см)
Ответ: 10см.
Слайд №10.

Что известно по условию задачи? Изобразите цилиндр так, чтобы осевое сечение было квадратом.
Решение.
Sосн=; BC=D;
=BC²=D²;
Sосн==3π.
Ответ: 3π.
Слайд №11.
Что известно по условию задачи?
Какое сечение построено?
Как найти расстояние от прямой до параллельной ей плоскости?
Выполняем рисунок.
Решение:
Из точки 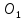 опустим перпендикуляр на АВ.
опустим перпендикуляр на АВ. 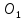 К – искомое расстояние. По теореме Пифагора из треугольника В
К – искомое расстояние. По теореме Пифагора из треугольника В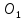 К
К 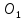 К=
К=;
∆А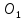 В – равнобедренный (А
В – равнобедренный (А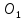 =В
=В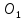 =R)
=R)
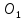 К – высота и медиана.
К – высота и медиана.
АК=ВК=
ВК==6 (см)
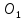 К=
К==8 (см)
Ответ: 8 см.
Задание на дом.
П. 52, 53. №1;2.
Итог урока.
Что нового сегодня, вы, узнали на уроке?
Слайд №12.
Спасибо за урок. Успехов в учёбе.

 Получите свидетельство
Получите свидетельство Вход
Вход











 "Цилиндр" конспект урока (4.56 MB)
"Цилиндр" конспект урока (4.56 MB)
 0
0 368
368 9
9 Нравится
0
Нравится
0



