Определение типичных ошибок выпускников при выполнении заданий ОГЭ
| № п/п | Основные проверяемые требования к математической подготовке | Коды поверяемых элементов содержания | Коды разделов элементов требований | Уровень сложности | Максимальный балл за выполнение задания | Примеры заданий | Краткое описание сути ошибки |
| Часть 2 | |||||||
| Модуль «Алгебра» | |||||||
| | Умение решать линейные и квадратные уравнения, системы линейных уравнений, линейные неравенства и их системы, квадратные и дробно-рациональные неравенства, в том числе при решении задач из других предметов и практических задач; умение использовать координатную прямую и координатную плоскость для изображения решений уравнений, неравенств и систем | 2,3 | 5 | П | 2 | Решите уравнение
| Ошибки при раскрытии скобок, используя формулы сокращенного умножения. Ошибки при решении квадратных уравнений (желательно всегда писать формулу) Вычислительные ошибки. |
| | Умение решать задачи разных типов; умение составлять выражения, уравнения, неравенства и системы по условию задачи, исследовать полученное решение | 3 | 8 | П | 2 | Рыболов в 5 часов утра на моторной лодке отправился от пристани против течения реки, через некоторое время бросил якорь, 2 часа ловил рыбу и вернулся обратно в 10 часов утра того же дня. На какое расстояние от пристани он отплыл, если скорость течения реки равна 2 км/ч, а собственная скорость лодки равна 6 км | Неверный ход решения задачи Забывают записывать единицы измерения к введенным значениям Не вводят переменные величины, а используют при составлении уравнений; -Путают понятия скорости и времени движения; -Допускают вычислительные ошибки; -Записывают ответ, используя приближения ( -Отсутствие краткой записи к решению задачи, и таблицы, и обоснований, решение задачи выглядит как столбик примеров без каких бы то ни было пояснений |
| | Умение строить графики функций, использовать графики для определения свойств процессов и зависимостей, для решения задач из других учебных предметов и реальной жизни; умение выражать формулами зависимости между величинами | 5 | 6 | В | 2 | Постройте график функции
определите, при каких значениях с прямая y=c имеет с графиком ровно одну общую точку. | -Отсутствуют деления на координатных осях, в результате чего график построен схематично и не проходит через точки, взятые в таблице значений; -Запись не соответствует построению, например, пишут: построим параболу, а строят ее часть и т.д.; -Путают линейную функцию с функцией прямой пропорциональной зависимости; Отсутствие таблиц значений для построения графиков, либо значения переменной(ых) найдены с ошибкой; Построение части графика функции, не являющейся линейной, по двум точкам и наоборот, построение части графика линейной функции по трем и более точкам; |
| Модуль «Геометрия» | |||||||
| | Умение применять формулы периметра и площади многоугольников, длины окружности и площади круга, объёма прямоугольного параллелепипеда; умение применять признаки равенства треугольников, теорему о сумме углов треугольника, теорему Пифагора, тригонометрические соотношения для вычисления длин, расстояний, площадей | 7 | 11 | П | 2 | В прямоугольном треугольнике ABC с прямым углом C известны катеты: A C 6, BC 8. Найдите медиану CK этого треугольника | Чертеж не соответствует условию задачи; -Допускают ошибки в чертежах, обозначение разных углов одинаковыми дугами, «пустые» чертежи…; -Отсутствие чертежа при решении геометрической задачи; - Не записывают обоснования к действиям геометрической задачи, отсутствуют ссылки на свойства, признаки, теоремы; -Допускают ошибки в пояснениях, например, используют признак равностороннего треугольника, а записывают по определению (в треугольнике все углы по 60 градусов, значит треугольник равносторонний по определению); |
| | Умение оперировать понятиями: определение, аксиома, теорема, доказательство; распознавать истинные и ложные высказывания, приводить примеры и контрпримеры, строить высказывания и отрицания высказываний | 7 | 2,11 | П | 2 | В параллелограмме ABCD точка E – середина стороны AB. Известно, что EC ED . Докажите, что данный параллелограмм – прямоугольник. | Ошибки при выполнении чертежа: изображение трапеции вместо параллелограмма; -Применение свойств несуществующей средней линии параллелограмма; -Путают признаки равенства треугольников с признаками подобия треугольников; -Используют не существующий признак равенства треугольников по трем углам, либо признак формулируют неверно, например, по двум углам и стороне между ними; -При доказательстве равенства элементов записывают неграмотные обоснования; -Не указывают признак по которому доказывают равенство треугольников; -Производят подмену геометрических понятий: путают отрезок и прямую; - Не указаны параллельные прямые при которых накрест лежащие углы равны, либо секущая при которой накрест лежащие углы образованы, либо неверное указание пары накрест лежащих углов (нет обоснования параллельности прямых); -При словесном обосновании действий недопустимы фразы вида: 2 угла лежат на одной стороне; -При введении обозначений их не описывают; -Решение задачи с другими данными; |
| | Умение применять формулы периметра и площади многоугольников, длины окружности и площади круга, объёма прямоугольного параллелепипеда; умение применять признаки равенства треугольников, теорему о сумме углов треугольника, теорему Пифагора, тригонометрические соотношения для вычисления длин, расстояний, площадей | 7 | 11 | В | 2 | Основание AC равнобедренного треугольника ABC равно 12. Окружность радиусом 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC. Найдите радиус окружности, вписанной в треугольник ABC. | Неверно построенный чертеж -Отсутствие доказательства геометрических фактов; -Отсутствие введения переменной (в случаях, когда величину отрезка обозначали переменной); -Арифметические ошибки при вычислениях
|

 Получите свидетельство
Получите свидетельство Вход
Вход


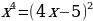
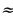 );
);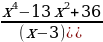









 Типичные ошибки при выполнении ОГЭ (21.82 KB)
Типичные ошибки при выполнении ОГЭ (21.82 KB)
 0
0 437
437 1
1 Нравится
0
Нравится
0










