Технологическая карта урока алгебры в 10 классе
Тема урока Метод рационализации в решении логарифмических неравенств
Тип урока Урок открытия нового знания.
Вид урока Комбинированный урок.
Формируемые результаты:
Предметные: формировать навык решения неравенств, используя метод рационализации.
Личностные: формировать умение представлять результат своей деятельности.
Метапредметные: формировать умение осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований.
Планируемые результаты. Учащийся научится решать логарифмические неравенства, сводя их к решению системы рациональных неравенств.
Основные понятия. Метод интервалов, область определения логарифмической функции..
Цели:
Деятельностная: формировать у учеников способность к рефлексии коррекционно-контрольного типа, научить детей находить причину своих затруднений, самостоятельно строить алгоритм действий по устранению затруднений, научить самоанализу действий и способам нахождения разрешения конфликта.
Содержательная: закрепить усвоенные знания, понятия, способы действия и скорректировать при необходимости.
Организационная структура урока
| Этап урока
| Деятельность учителя | Деятельность учащихся | |||||||||||||||||||||||||||||||||||||||
| 1.
| Этап мотивации (самоопределения) к учебной деятельности Главная задача этого этапа — создать такие условия, чтобы ученик внутреннее собрался, подготовился и нацелился на «покорение новых вершин».
| ||||||||||||||||||||||||||||||||||||||||
| Учитель использует все три пласта мотивации: «хочу» — вызываем интерес к уроку, к деятельности (цитата) Как вы понимаете слова Вольтера: «Работа избавляет нас от 3 великих зол: скуки порока, нужды»; «надо» — подводим ученика к осознанию важности и необходимости нового знания (логарифмические неравенства будут на промежуточной аттестации и задание № 15 на ЕГЭ); «могу» — определяем тематические рамки познания, (непосильных и сверхсложных задач не предвидится).
| Возможный ответ учащегося: «Данное высказывание заставляет задуматься, Я согласен с мнением автора. Я уверен, что смысл данного высказывания состоит в том, что труд - это та деятельность, которая благотворно влияет на человека. Труд даёт нам материальные блага, эмоциональное удовлетворение и качественное времяпровождение. Труд заставляет людей забывать о своих проблемах, он увлекает с головой. Я считаю, что труд - это то, что необходимо каждому из нас» | ||||||||||||||||||||||||||||||||||||||||
| 2. | Актуализация и фиксирование индивидуального затруднения в пробном действии Основная цель данного этапа заключается в том, чтобы каждый ученик внутренне осознал потребность открытия новых знаний и умений. А пробное действие позволит каждому зафиксировать свои, индивидуальные затруднения. | ||||||||||||||||||||||||||||||||||||||||
| 1.Заполни таблицу
2. Решите неравенства: а) (х – 1)(х +4)≥ 0, б) log3(3x – 1) log3(2x + 3)
- Какие задания вызвали затруднение? Почему?
| Ответы. 1.
2. а) ( - ∞; - 4]U [1; + ∞) б) (1/3; 4) Взаимопроверка решений, заполнение Таблицы успеха. Выяснение причин затруднения. Ликвидация пробелов в знаниях.
| ||||||||||||||||||||||||||||||||||||||||
| 3. | Этап выявления места и причины затруднений. Главная цель этого этапа: дать возможность ученикам осознать, в чем именно состоит затруднение, каких знаний, умений и навыков им не хватает для решения пробного задания.
| ||||||||||||||||||||||||||||||||||||||||
| - Какое из неравенств решить легче?
- Как вы думаете, можно ли решение логарифмическое неравенства свести к решению рациональных неравенств без использования монотонности функции?
| - Рациональное.
Учащиеся высказывают свои гипотезы.
Ученики анализируют свои попытки выполнить пробное задание, проговаривают вслух: что и как они делали. В ходе анализа каждый фиксирует для себя тот шаг, тот момент в решении, на котором они «споткнулись» — это место затруднения. «Озарение» не состоялось. Осознание затруднения: не смогли составить рациональное неравенство, чтобы оно учитывало монотонность.
| ||||||||||||||||||||||||||||||||||||||||
| 4. | Этап построение проекта выхода из создавшейся ситуации. Основная цель этого этапа: формулировка главных целей и темы урока, выбор способа разрешения проблемы, выбор метода и средств. | ||||||||||||||||||||||||||||||||||||||||
| - Сформулируйте тему урока
- Сформулируйте цель урока
- Общими усилиями попытаемся справиться с возникшим затруднением. Найдите знаки выражений F(x) = logaf(x) – logag(x), f(x) – g(x) и G(x) = (a – 1)(f(x) – g(x))
- Проанализируйте заполненную таблицу и сделайте вывод.
- Что категорически нельзя забывать, работая с логарифмами?
- Сформулируйте окончательный вывод.
Полученный результат запишем в виде теоремы. Теорема. При а0 и а ≠ 1 знаки выражений logaf(x) – logag(x) и (a – 1)(f(x) – g(x)) совпадают для всех значений х таких, что f(х) 0 и g(x) 0.
| - Рационализации при решении логарифмических неравенств
- Научится решать логарифмические неравенства, сводя их к решению рациональных неравенств.
Учащиеся заполняют таблицу:
- Из таблицы следует, что выражения F(x) и G(x) имеют одинаковые знаки! - Про область определения логарифмической функции. - Выражения F(x) и G(x) ПРИ ВСЕХ ДОПУСТИМЫХ ЗНАЧЕНИЯХ Х имеют одинаковые знаки.
Учащиеся записывают теорему в тетрадь. | ||||||||||||||||||||||||||||||||||||||||
| 5. | Реализация построенного проекта Главная цель этого этапа: ученики сами создают проект выхода и пробуют применить его на практике. Здесь важно, чтобы выбранное новое действие было способно разрешить не только то затруднение, которое было уже зафиксировано, но решать все задачи подобного типа. | ||||||||||||||||||||||||||||||||||||||||
| Записать неравенство в виде logaf(x) – logag(x) v 0, заменить его равносильной системой рациональных неравенств: 2) |
Решается учениками на доске с комментариями.
| ||||||||||||||||||||||||||||||||||||||||
| 6. | Этап первичного закрепления с проговариванием во внешней речи На данном этапе ученикам предлагается несколько типовых задач по новой теме. | ||||||||||||||||||||||||||||||||||||||||
| Записать неравенство в виде системы рациональных неравенств. 2. Решить неравенство
| Ученики в парах решают задания по новому, выработанному проекту и обязательно проговаривают каждый этап, объясняют и аргументируют свои действия. Решение. Составляем систему рациональных неравенств, аналогичную системе: | ||||||||||||||||||||||||||||||||||||||||
| 7. | Этап самостоятельной работы с проверкой по эталону
| ||||||||||||||||||||||||||||||||||||||||
| I. Запишите неравенство в виде системы рациональных неравенств:
. 2. Решить неравенство методом рационализации
| Четверо учащихся решают на обратной стороне откидных досок. Остальные ученики самостоятельно выполняют типовые задания, проверяют их по предложенному эталону сначала сами, затем друг у друга. 2. | ||||||||||||||||||||||||||||||||||||||||
| 8. | Этап включения в систему знаний и повторения Основная цель этого этапа: зафиксировать полученное знание, рассмотреть, как новое знание укладывается в систему ранее изученного, при возможности довести полученный навык до автоматизированности использования и подготовить учеников к дальнейшему погружению в тему. | ||||||||||||||||||||||||||||||||||||||||
| Для каких неравенств применяется этот метод? Почему этот метод называется «рационализация»? В чём состоит эта рационализация? Каковы рамки применения нового метода? Обязательна ли разность функций? Обязательна ли монотонность функций? - | Учащиеся отвечают на вопросы | ||||||||||||||||||||||||||||||||||||||||
| 9. | Этап рефлексии учебной деятельности на уроке На данном этапе ученики соотносят цели, которые они ставили на уроке и результаты своей деятельности. | ||||||||||||||||||||||||||||||||||||||||
| Прием: Таблица "+ - " Вопросы для рефлексии Замена логарифмического неравенства равносильной системой. Решение линейных неравенств. Решение квадратных неравенств Метод интервалов. Цель достигнута?
Домашнее задание: § 6. № 114 или № 118 решить методом рационализации.
| Заполнение Таблицы успеха. В столбце рефлексии ставят + или -. | ||||||||||||||||||||||||||||||||||||||||
Список используемой литературы:
Алгебра и начала математического анализа. А45 10 класс : учеб. для общеобразоват. учреждений : базовый и профил. уровни / [Ю. М. Колягин, М. В. Ткачева, Н. Е. Федорова, М. И. Ш абунин]; под ред. А . Б. Ж ижченко. — 4-е изд. — М. : Просвещение, 2011.— 368 с. : ил.— ISBN 978-5-09-025401-4..
А.Г. Корянов, А.А. Прокофьев. Материалы курса «Готовим к ЕГЭ хорошистов и отличников»: лекции 1-4. – М.: Педагогический университет «Первое сентября», 2012.

 Получите свидетельство
Получите свидетельство Вход
Вход



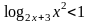
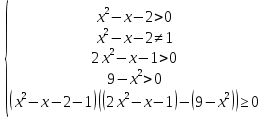
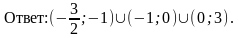
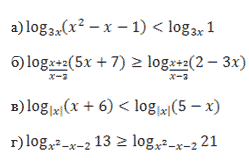









 Технологическая карта урока алгебры "Метод рационализации в решении логарифмических неравенств" (53.35 KB)
Технологическая карта урока алгебры "Метод рационализации в решении логарифмических неравенств" (53.35 KB)
 0
0 263
263 33
33 Нравится
0
Нравится
0


