Теорема синусов — теорема, которая устанавливает зависимость: стороны треугольника - противолежащие им углы.
Теорема синусов: Стороны треугольника пропорциональны синусам противолежащих углов.
Есть 2 подвида теоремы: обычная и расширенная теорема синусов.
Обычная теорема синусов:
Стороны треугольника пропорциональны sin противоположных углов.
a/sinα=b/sinβ=c/sinγ.
Расширенная теорема синусов для произвольного треугольника:

a/sinα=b/sinβ=c/sinγ=2*R
где a, b, c — стороны треугольника, α, β, γ — противолежащие этим сторонам углы, а R — радиус окружности, которая описана вокруг треугольника.
Доказательство теоремы синусов.
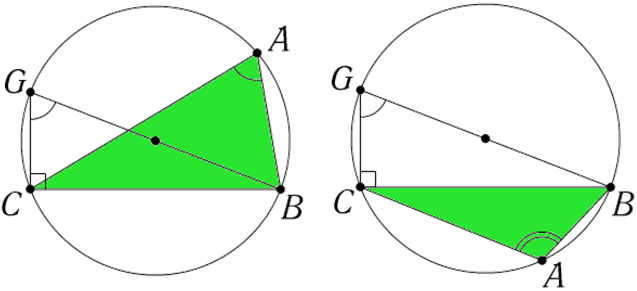
Пусть есть треугольник, вписанный в окружность. Обозначим его как ABC.
Что бы доказать всю теорему, так как треугольник имеет произвольные размеры, можно доказать только то, что соотношение 1-ной произвольной стороны к противолежащему углу соответствует 2R.
Допустим, это будет 2R = a/sin α, т.е. если смотреть по чертежу 2R = BC / sin A.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход


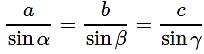
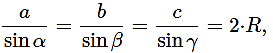
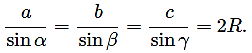









 Теорема синусов (методический материал) (0.1 MB)
Теорема синусов (методический материал) (0.1 MB)
 0
0 1044
1044 71
71 Нравится
0
Нравится
0










