Тематический материал по информатике для подготовки учащихся к ЕГЭ

Раздел 1. Информационные процессы и системы

Тема 1. Информация и ее кодирование

Вероятный подход к определению количества информации.

1. Понятие «Количество информации».

Можно ли измерить количество информации.

Существует 2 подхода к измерению информации: один из них называется содержательный или вероятностный.

Сообщение несет больше информации, если в нем содержатся новые и понятные сведения. Такое сообщение называется информативным.

Содержит ли информацию учебник физики за 10класс? (Да)

Для кого он будет информативным – для ученика 10 класса или 1 класса? (Для ученика 10 класса он будет информативным, т.к. в нем содержится новая и понятная информация, а для ученика 1 класса он информативным не будет, т.к. информация для него не понятна).

Вывод: количество информации зависит от информативности.

Количество информации равно 0, если с точки зрения конкретного человека сообщение неинформативно.

В информативном сообщении, количество информации больше нуля.

2. Понятие вероятного подхода в измерении информации.

Если некоторое сообщение является информативным, значит оно пополняет нас знаниями уменьшает неопределенность наших знаний.

Пример 1: мы бросаем монету, попытаемся угадать, какой стороной она упадет на поверхность.

Возможен один результат из двух: «орел» или «решка». Каждое событие является равновероятным.

Перед броском монеты существует неопределенность наших знаний (возможно одно событие из двух), а после броска наступает полная определенность.

Вывод: из двух равновероятных событий произошло одно.

Пример 2: кидаем шестигранный кубик. В этом случае возможно получить один вариант из шести равновероятных.

Неопределенность знаний равна 6. после броска кубика неопределенность знаний уменьшается в 6 раз.

Пример 3: (устно).

На экзамен приготовлено 36 билетов.

Чему равно количество событий, которые могут произойти при вытягивании билета? (36)

Равновероятны эти события? (Да)

Чему равна неопределенность знаний ученика при вытягивании билета? (36)

Во сколько раз уменьшается неопределенность знаний после вытягивании билета (в 36 раз)

Зависит ли это от номера вытянутого билета (Нет, т. К. события равновероятны)

Вывод:

Мы не получаем информации в ситуации, когда происходит одно событие из одного возможного. Количество информации в этом случае равно 0.

Для того, чтобы количество информации имело положительное значение, необходимо получить сообщение о том, что произошло событие, как минимум из двух равновероятных.

Весь материал - в документе.

Автор - составитель Мызникова И. В.

Тематический материал

для подготовки учащихся к ЕГЭ по информатике

Раздел 1. Информационные процессы и системы Тема 1. Информация и ее кодирование Вероятный подход к определению количества информации.

1. Понятие «Количество информации».

Можно ли измерить количество информации.

Существует 2 подхода к измерению информации: один из них называется содержательный или вероятностный.

Сообщение несет больше информации, если в нем содержатся новые и понятные сведения. Такое сообщение называется информативным.

• Содержит ли информацию учебник физики за 10класс? (Да)

• Для кого он будет информативным – для ученика 10 класса или 1 класса? (Для ученика 10 класса он будет информативным, т.к. в нем содержится новая и понятная информация, а для ученика 1 класса он информативным не будет, т.к. информация для него не понятна).

Вывод: количество информации зависит от информативности.

Количество информации равно 0, если с точки зрения конкретного человека сообщение неинформативно.

В информативном сообщении, количество информации больше нуля.

2. Понятие вероятного подхода в измерении информации.

Если некоторое сообщение является информативным, значит оно пополняет нас знаниями  уменьшает неопределенность наших знаний.

Пример 1: мы бросаем монету, попытаемся угадать, какой стороной она упадет на поверхность.

Возможен один результат из двух: «орел» или «решка». Каждое событие является равновероятным.

Перед броском монеты существует неопределенность наших знаний (возможно одно событие из двух), а после броска наступает полная определенность.

Вывод: из двух равновероятных событий произошло одно.

Пример 2: кидаем шестигранный кубик. В этом случае возможно получить один вариант из шести равновероятных.

Неопределенность знаний равна 6. после броска кубика неопределенность знаний уменьшается в 6 раз.

Пример 3: (устно).

На экзамен приготовлено 36 билетов.

• Чему равно количество событий, которые могут произойти при вытягивании билета? (36)

• Равновероятны эти события? (Да)

• Чему равна неопределенность знаний ученика при вытягивании билета? (36)

• Во сколько раз уменьшается неопределенность знаний после вытягивании билета (в 36 раз)

• Зависит ли это от номера вытянутого билета (Нет, т. К. события равновероятны)

Вывод:

Мы не получаем информации в ситуации, когда происходит одно событие из одного возможного. Количество информации в этом случае равно 0.

Для того, чтобы количество информации имело положительное значение, необходимо получить сообщение о том, что произошло событие, как минимум из двух равновероятных.

Такое количество информации, которое находится в сообщении о том, что произошло одно событие из двух равновероятных, принято за единицу измерения информации и равно 1 биту.

1 бит – это количество информации, уменьшающее неопределенность знаний в 2 раза.

Игра «Угадай число»

Загадайте какое – нибудь число из заданного интервала.

Стратегия поиска: необходимо на каждом шаге в два раза уменьшать неопределенность знаний, т. Е. задавать вопросы, делящие числовой интервал на 2. Тогда ответ «Да» или «Нет» будет содержать 1 бит информации

Загадано число «5» из интервала от 1 до 16

Вопрос	Ответ	Неопределенность знаний	Полученное количество информации
Число больше 8?	Нет	8	1 бит
Число больше 4?	Да	4	1 бит
Число больше 6?	Нет	2	1 бит
Число5?	Да	1	1 бит
Итого:			4 бит

Я загадала число (8) от 1 до 32. Угадайте его. Я знаю какое количество бит информации получится (5)

Вопрос	Ответ	Неопределенность знаний	Полученное количество информации
Число больше 16?	Нет	8	1 бит
Число больше 8?	Нет	4	1 бит
Число больше 4?	Да	2	1 бит
Число больше 6?	Да	1	1 бит
Число меньше 8? Число 8.	Нет		1 бит
Итого:			5 бит

Существует формула, которая связывает между собой количество возможных событий и количество информации.

N=2^L

L=log₂N

N – Количество возможных вариантов

L – Количество информации

В разобранном примере N=32

L= log₂32

L=5

Пример1: Какое количество информации можно получить при угадывании числа из интервала от 1 до 11

N=11

L= log₂11 L=3,45943

Пример2: Какое количество информации можно получить в игре «крестики- нолики» на поле 3*3? N=9 log₂9=3,16993

4*4 N=16 log₂16=4

3.Неравновероятные события

В жизни существует множество неравновероятных событий.

Например:

• Если вы лучший ученик в классе, то вероятность получить оценку «5» за контрольную выше чем вероятность получить оценку «2»

• Нельзя сказать с равной степенью вероятности, что дождь будет и зимой и летом. Скорее всего, это событие вероятнее летом чем зимой

L=log₂ (1/p)

L-количество информации

p=K/N - вероятность

K- величина, показывающая, сколько раз произошло интересующее нас событие.

N- общее число возможных исходов какого-то процесса.

Решение задач по теме «Вероятный подход»

1. «Вы выходите на следующей остановке?» - спросили человека в автобусе. «Нет», - ответил он. Сколько информации содержит ответ?

Решение: Возможны два варианта ответов «Да» и «Нет»

N=2

2=2¹ Количество информации равно 1

Ответ: 1 бит

1. Какой объем информации содержит сообщение, уменьшающее неопределенность знаний в 4 раза?

Решение: N=4

4=2² Количество информации равно 2

Ответ: 2 бит

1. Вы подошли к светофору, когда горел желтый свет. После этого загорелся зелёный. Какое количество информации вы при этом получили?

Решение: N=2 (2 сигнала светофора по условию задачи)

2=2¹ Количество информации равно 2

Ответ: 2 бит

1. Группа школьников пришла в бассейн, в котором 4 дорожки для плавания. Тренер сообщил, что группа будет плавать на дорожке номер 3. Сколько информации получили школьники из этого сообщения?

Решение: N=4

4=2² Количество информации равно 2, оно не зависит от номера дорожки.

Ответ: 2 бит

1. В корзине лежат 8 шаров. Все шары разного цвета. Сколько информации несет сообщение о том, что из корзины достали красный шар?

Решение:

8=2³ Количество информации равно 3

Ответ: 3 бит

1. Была получена телеграмма: «Встречайте, вагон 7». Известно, что в составе поезда 16 вагонов. Какое количество информации было получено?

N=16

16=2⁴ Количество информации равно 4 бит. Номер вагона 7 не влияет на определение количества информации.

Ответ: 4 бит

1. При угадывании целого числа в диапазоне от 1 до N было получено 7 бит информации. Чему равно N?

Решение: L=7 бит

N=2⁷ N=128

Ответ: 128

1. Сообщение о том, что ваш друг живёт на 10 этаже, несёт 4 бита информации. Сколько этажей в доме?

Решение:

N=4

N=2⁴ N=16

Ответ: 16 этажей

1. Сообщение о том, что Петя живёт во втором подъезде, несёт 3 бита информации. Сколько подъездов в доме?

Решение: L=3 бит

N=2³ N=8

Ответ: 8 подъездов

1. Какое количество информации несет сообщение: «Встреча назначена на сентябрь?»

Решение: в году 12 месяцев

12=2^L L=log₂12(16)=4 бит

Ответ: 6 бит

1. Какое количество информации несет сообщение о том, что встреча назначена на 15 число?»

Решение: в месяце 30 дней

N=30

30=2^L L=log₂30(32)=5 бит

Ответ: 5 бит

1. Какое количество информации несет сообщение о том, что встреча назначена на 23 октября в 15.00?

Решение: 23 октября 24 часа

24=2^L L=log₂24(32)=5 бит

Ответ: 5 бит

1. В школьной библиотеке 16 стеллажей с книгами. На каждом стеллаже 8 полок. Библиотекарь сообщил Пете, что нужная ему книга находится на пятом стеллаже на третьей сверху полке. Какое количество информации библиотекарь передал Пете?

Решение:

Определим сколько всего полок

16*8=128

128=2^L L=7

бит

1. В корзине лежат 8 черных шаров и 24 белых. Сколько информации несет сообщение о том, что достали черный шар?

Дано: K₁=8 K₂=24

Найти: L

Решение:

N=8+24=32

P=8/32=1/4

L=log₂(4)=2 бит

Ответ: 2 бита

1. В коробке лежат 64 цветных карандаша. Сообщение о том, что из коробки достали белый карандаш, несёт 4 бита информации. Сколько белых карандашей было в корзине?

Дано: N=64 L=4

Найти: К

Решение:

L=log₂(1/p) p=K/N

4=log₂(1/p)

1/p=2⁴

1/p=16

P=1/16

1/16=K/64

K=4

Ответ: 4 белых карандаша

1. В классе 30 человек. За контрольную работу по математике получено 15 «5», 6 «4», 8 «3» и 1 «2». Какое количество информации в сообщении о том, что Андреев получил пятерку.

Дано: N=30 K₅=15 K₄=6 K₃=8 K₂=1

Найти: L

Решение:

P=15/30=1/2 – вероятность получения «5»

L=log₂(1*2/1)=1 бит

Ответ: 1 бит

1. На остановке останавливаются автобусы с разными номерами. Сообщение о том, что к остановке подошел автобус с номером N1 несет 4 бита информации. Вероятность появления на остановке автобуса с номером N2 в два раза меньше, чем вероятность появления автобуса с номером N1. Сколько информации несет сообщение о появлении автобуса с номером N2.

Дано: L_N1=4 бита

p_N2=1/2*p_N1

Найти: L_N2

Решение:

L_N1=log₂(1/p_N1)

L_N2=log₂(1/p_N2)

1/p_N1=2^L1

1/p_N1=2⁴

1/p_N1=16

P_N1=1/16

P_N2=1/2*1/16

P_N2=1/32

L_N2=log₂32

L_N2=5 бит

Ответ: 5бит

Алфавитный подход к измерению информации.

Другой подход измерения информации – алфавитный.

Каким образом в этом случае можно найти количество информации.

Рассмотрим пример:

У нас небольшой текст, написанный на русском языке. Он состоит из букв русского алфавита, цифр, знаков препинания. Для простоты будем считать, что символы в тексте присутствуют с одинаковой вероятностью.

Множество используемых в тексте символов называется алфавитом. В информатике под алфавитом понимают не только буквы, но и цифры, и знаки препинания, и другие специальные знаки. У алфавита есть размер (полное количество символов), который называется мощностью алфавита.

Обозначим мощность алфавита через N. Тогда воспользуемся формулой для нахождения количества информации их вероятностного подхода: L=log₂N.

Для расчета количества информации по этой формуле нам необходимо найти мощность алфавита N.

Правило для измерения информации с точки зрения алфавитного подхода.

1. Найти мощность алфавита N.

2. Найти информационный объем одного символа - L=log₂N.

3. Найти количество символов в сообщении – K.

4. Найти информационный объем всего сообщения – K*N.

Пример 1:

Найти объем информации, содержащийся в тексте из 3000 символов, написанный русскими буквами. (К=3000)

Решение:

1. Найдем мощность алфавита N

N=33 русских прописных буквы+33 русских строчных буквы+21 специальный знак=87 символов

1. Рассчитаем количество информации L

L=log₂87=6,4 бита – несет один символ в русском тексте

1. Найдем информационный объем всего сообщения K*L

6,4*3000=19140 бит

Пример 2:

Найти количество информации, содержащейся в немецком тексте с таким же количеством символов

Решение:

1. Найдем мощность алфавита N

N=26 немецких прописных буквы +26 немецких строчных буквы+21 специальный знак =73 символа

1. Рассчитаем количество информации L

L=log₂73=6.1 бит- информационный объем одного символа

1. Найдем информационный объем всего сообщения K*L

6.1*3000=18300 бит

Пример 3:

Найти объем текста, записанного на языке , алфавит которого содержит 128 символов и 2000 символов в сообщении.

Дано:

Найти:

Решение:

1) L=log₂128=7 бит – объем одного символа

2) L_т=L*K=7*2000=14000 бит – объем сообщения

Ответ: 14000 бит

Единицы измерения информации

В компьютере также используется свой алфавит, который можно назвать компьютерным. Количество символов, которое в него входит, равно 256 символов.

Это мощность компьютерного алфавита. Также мы выяснили, что закодировать 256 разных символов можно с помощью 8 бит. 8 бит является настолько характерной величиной, что ей присвоили свое название – байт.

Итак, следующая по величине единица измерения информации – байт.

1 байт = 8 битам.

Пример 4:

Найти информационный объем страницы компьютерного текста.

Пояснение: текст состоит из 50 строк, в каждой строке 40 символов.

Решение:

1. Найдем информационный объем одного символа:

L=log₂256=8 бит=1 байт

1. Найдем количество символов на странице.

40*50=2000 байт

1. Найдем информационный объем всей страницы

Ответ: 2000 байт.

Для измерения больших объемов информации используют следующие единицы:

1 килобайт=1Кб=2¹⁰байт=1024 байта

1 мегабайт=1Мб=2¹⁰Кб=1024 Кб

1 гигабайт=1Гб=2¹⁰Мб=1024 Мб

Задание:

Выразите:

- 3 Кбайта в байтах и битах; 3кб=3*1024 байт=3072 байта=3072*8 бит=24576 бит

- 81920 бит в байтах и Кбайтах 81920 бит=10240 байт=10 кбайт

- 3072 Мбайта в Гбайтах и Кбайтах 3072 Мбайт=3 Гбайт=3072*1024 Кбайт

таблица «Измерение информации»

Вероятный подход		Алфавитный подход
Вероятные события	Невероятные события
N – число возможных событий N=2L	N – число возможных событий N=2L	N – мощность алфавита (полное количество символов) N(русский текст)=33прописных буквы+33строчных буквы+21специальный символ=87 символов N(немецкий текст)=26+26+21=73 символов N(английский текст)=73 символа N(компьютерный текст)=256 символов
L –количество информации L=log2N Количество информации = неопределенности знаний	L –количество информации	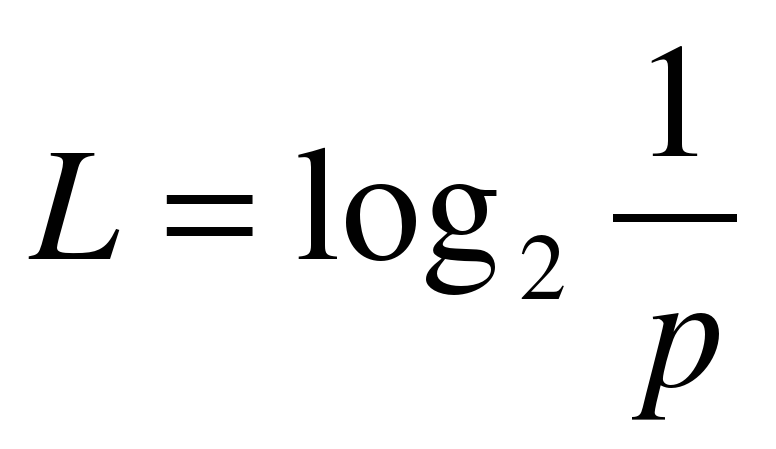L – информационный объем одного символа L=log2N
	P - вероятность событий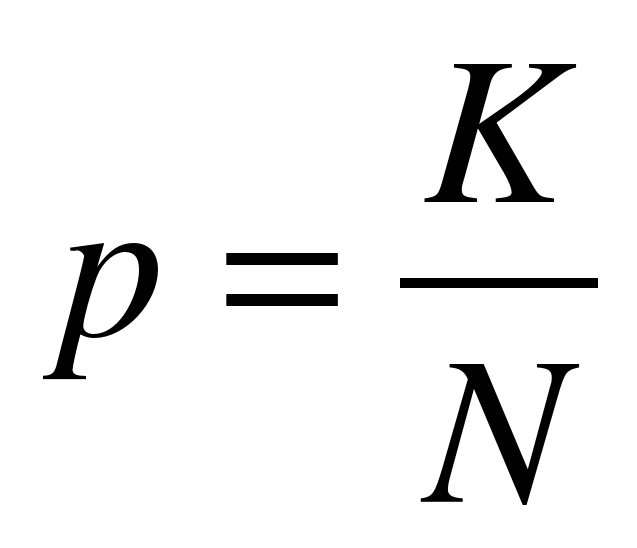
	К – число известных событий	К – количество символов в сообщении
		L*K-информационный объем сообщения
Пример1: Какое количество информации содержится в сообщении о том, что упала монета определенной стороной? Число возможных вариантов 2. N=2 Количество информации, которое несет сообщение L=log22=1 бит Пример 2: Чему равна неопределенность знаний при угадывании карты из колоды в количестве 32 штук? L=log232=5 бит	Пример: В корзине 13 белых шаров, 11 красных и 2 черных. Определить количество информации, которое несет сообщение о том, что из корзины достали белый шар? 1. Число шаров в корзине N=13+11+2=26 2. Вероятность доставания белого шара р=13/26=1/2 3. Количество информации 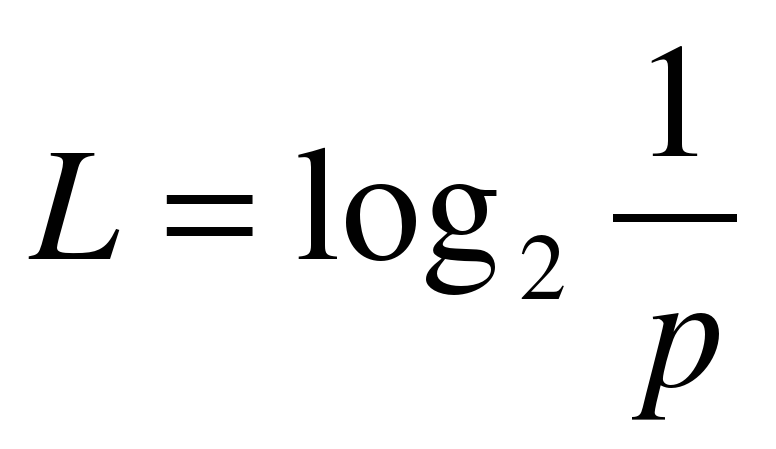, L=log22=1бит	Пример: Определить информационный объем сообщения написанного на русском языке, состоящего из 3000 символов. Мощность алфавита N=87 Определим информационный объем одного символа L=log2N, L=log287=6,4 бит 3. Информационный объем сообщения L*N=6,4*3000=19200 бит

Единицы измерения информации

8 бит = 1 байт

1 кбайт = 1024 байт

1Мбайт = 1024 кбайт

1 Гбайт = 1024 Мбайт

Решение задач по теме «Информация и её кодирование»

1. Сколько бит информации содержит сообщение объемом 4 мегабайта?

Решение:

4 Мбайт=4*1024 к байт=4*1024*1024 байт=4*1024*1024*8 бит

2²*2¹⁰*2¹⁰*2³=2²⁵ бит

1. Сколько мегабайт содержит сообщение объемом 2²³бит.

Решение:

2²³=2¹⁰*2¹⁰*2³=1024*1024*8=1Мбайт

1. Метеорологическая станция ведет наблюдение за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100%, которое записывается при помощи минимально возможного количества бит. Станция сделала 80 измерений. Определите информационный объем результатов наблюдений.

Решение:

N(мощность алфавита)=101

L(информационный объем одного измерения)=log₂N

L=log₂101

2⁶⁷ возьмем 2⁷

L=log₂2⁷=7

Информационный объем сообщения K*L=7*80=560 бит или 70 байт

1. Автоматическое устройство осуществило перекодировку информационного сообщения на русском языке, первоначально записанного в 16 битном коде Unicode, в 8 битную кодировку КОИ – 8. При этом информационное сообщение уменьшилось на 240 бит. Какова длина сообщения в символах?

Решение:

Пусть в первоначальном сообщении Х символов.

16 бит*Х=16*Х бит

В перекодированном сообщении количество символов не изменилось, т. е. оно = Х

8 бит*Х=18*Х=18Хбит

16Х-8Х=240

8Х=240

Х=30 символов

1. Азбука Морзе позволяет кодировать символы для радиосвязи, задавая комбинацию точек и тире. Сколько различных символов (цифр, букв, знаков пунктуации и т. д.) можно закодировать, используя код Морзе длиной не менее пяти и не более шести сигналов (точек и тире)?

Решение:

К₁+К₂=2⁵+2⁶=32+64=96 сигналов

1. Для передачи секретного сообщения используется код, состоящий из строчных и прописных букв латинского алфавита. При этом все цифры кодируются одним и тем же (минимально возможным) количеством бит. Определите информационный объем сообщения длиной в 100 см.

N(мощность алфавита)=26+26=52

L(инф. Объем одного символа)=log₂52

2⁵=32 мало 2⁵⁶

2⁶=64

K*L=6*100=600 бит

1. В кодировке Unicode на каждый символ на каждый символ отводится два байта. Определите информационный объем слова из двадцати четырех символов в этой кодировке.

Решение:

1 символ – 2 байта

1 байта – 8 бит

2 байта – 16 бит

16 бит*24 символа=384 бит

1. Световое табло состоит из лампочек. Каждая лампочка может находиться в одном из трёх состояний (включено, выключено или мигает). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 18 различных сигналов.

Решение:

n лампочек дают 3ⁿ различных комбинаций

3²=9 (двух лампочек мало, т. к. всего 9 сигналов)

3³=27 (три лампочки дают 27 сигналов)

9

1. Для передачи секретного сообщения используется код, состоящий из десятичных цифр. При этом все цифры кодируются одним и тем же (минимально возможным) количеством бит. Определите информационный объем сообщения длиной в 150 символов.

Решение:

2³=8, мало, надо 10

2⁴=16

8

4*150=600 – информационный объем сообщения

1. В кодировке ASCII на каждый символов отводится один байт. Определите информационный объем следующего высказывания Рене Декарта: Я мыслю, следовательно, существую.

Решение:

Подсчитаем количество символов в предложении, учитывая все знаки препинания и пробелы

34 символа

34*1 байт=34 байт или 34*8 =272 бит

1. Световое табло состоит из лампочек, каждая из которых может находиться в двух состояниях (включено или выключено). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 1000 различных сигналов.

Решение:

n-лампочек

2-состояния

1000-символов

2ⁿ 2⁹=512 2¹⁰=1024

2⁹¹⁰

10 лампочек

1. В велокроссе участвуют 459 спортсменов. Специальное устройство регистрирует прохождение каждым из участников промежуточного финиша, записывая его номер с использованием минимально возможного количества бит, одинакового дл каждого спортсмена. Каков информационный объем сообщения, записанного устройством, после того, как промежуточный финиш прошли 160 велосипедистов?

Дано: N=459, K=160

Найти: L*K -?

Решение:

L=log₂459 (512)

L=9

K*L=9*160=1440 бит

1440/8=180 байт

1. Скорость передачи данных через ADSL – соединение равна 128000 бит/с. Передача файла через это соединение заняла 2 мин. Определите размер файла в килобайтах.

Решение:

Размер файла=скорость*время передачи

Выразим скорость в килобайт/с

128000 бит/с 128000/8=16000 байт/с 16000/1024=15,625 кбайт/с

Выразим время через секунды

2 мин=2*60=120 с

Размер файла равен 15,625*120=1875 кбайт

1. В соревновании участвуют 220 атлетов. Какое минимальное количество бит необходимо, чтобы кодировать номер

Решение:

N=2^L

220=2^L

L=log₂220

2⁷=128 2⁷⁸

2⁸=256

L=log₂2⁸

L=8 бит

Системы счислений.

Системы счислений бывают непозиционные и позиционные.

Непозиционные – от положения цифры в числе не зависит ее величина.

Примером непозиционных систем счислений является Римская система.

I V X L C D M

1 5 10 50 100 500 1000

CCXXXII=2*100+3*10+2*1=232

IV=6

Позиционные системы – от позиции цифры в числе зависит ее величина

Современная система счисления, используемая в математике, является десятичной позиционной системой. Ее основание n=10, т. к. любую комбинацию чисел можно составить из 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

В системах счисления с основанием nn10 – к арабским числам прибавляются латинские буквы.

основание	название	алфавит
n=2	двоичная	0,1
n=3	троичная	0,1,2
n=8	восьмеричная	0,1,2,3,4,5,6,7,8
n=16	шестнадцатеричная	01,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F

Примеры:

1. Записать десятичные числа в развернутом виде

12456₁₀=1+10⁴+2*10³+4*10²+5*10¹+6*10⁰

678,45₁₀=6*10²+7*10¹+8*10⁰+4*10^-1+5*10^-2

1. Получить числа в десятичной системе

112₃=1*3²+1*3¹+2*3⁰=14₁₀

1001011₂=1*2⁶+0*2⁵+0*2⁴+1*2³+0*2²+1*2¹+1*2⁰=64+8+2+1=75₁₀

Перевод десятичных чисел в другие системы счисления

1. Перевод целых чисел

Алгоритм

1.Последовательно выполнять деление данного числа и получаемых неполных частных на основание новой системы счисления, пока не получим новое частное, меньше делителя

2.Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления

3.Составить число в новой системе счисления, записывая его, начиная с последнего частного.

Примеры:

14₁₀ -A₃=112₃

14	3
12	4	3
2	3	1
	1

75₁₀-А₂=1001011₂

75	2
74	37	2
1	36	18	2		2
	1	18	9	2
0			8	4
			1	4	2	2
				0	2	1
			0

1. Перевод дробных чисел

Алгоритм

1.Последоавательно умножать данное число и получаемые дробные части произведений на основание новой системы счисления до тех пор, пока дробная часть не станет равной нулю или не будет достигнута требуемая точность представления числа в новой системе счисления.

2.Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствии с алфавитом новой системы счисления

3.Составить дробную часть числа новой системы счисления, начиная с целой части первого произведения.

Примеры:

1. 0,1875₁₀-А₈=0,14₈

0	1875
*	8
1	5
*	8
4	0

2. 0,1875₁₀-А₂=0,0011₂

0	1875
*	2
0	3750
*	2
0	7500
*	2
1	5000
*	2
1	0000

3. 0,1875₁₀-А₁₆=0,3

0	1875
*	16
1 +1	1250 875
3	0000

1. Перевод смешанных чисел

Алгоритм:

Разбить число на целую и дробную части и применить соответствующие алгоритмы

Пример:

75,1875₁₀-1001011, 0011₂

Решить самостоятельно:

523₁₀-A₃

856₁₀-A₈

0,745₁₀-A₁₆

78,333₁₀-A₃

31₈-A₁₀

Перевод чисел из двоичной системы в восьмеричную и шестнадцатеричную системы и наоборот

	8=23	16=24
0	000	0000
1	001	0001
2	010	0010
3	011	0011
4	100	0100
5	101	0101
6	110	0110
7	111	0111
8		1000
9		1001
A		1010
B		1011
C		1100
D		1101
E		1110
F		1111

Перевод целых чисел

Для того, чтобы целое двоичное число записать в системе счисления с основанием q=2ⁿ (4, 8, 16, и т. д.) нужно:

1.данное двоичное число разбить справа налево на группы по n цифр в каждой;

2.если в последней левой группе окажется меньше n разрядов, то ее надо дополнить слева нулями до нужного числа разрядов

3. рассмотреть каждую группу как n – разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q=2ⁿ

Примеры:

1. 110111100111001₂-A₈ Разделим данное число на группы по три цифры (8=2³), начиная справа

110 111 100 111 001₂=67471₈

2. 111100111001₂-A₁₆ Разделим данное число на группы по четыре цифры (16=2⁴), начиная справа

0110 1111 0011 1001₂=6F39₁₆

Перевод дробных чисел

Для того, чтобы дробное двоичное число записать в системе счисления с основанием q=2ⁿ (4, 8, 16, и т. д.) нужно:

1. данное двоичное число разбить слева на право на группы по n цифр в каждой;

2. если в последней правой группе окажется меньше n разрядов, то ее надо дополнить нулями до нужного числа разрядов;

3. рассмотреть каждую группу как n – разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q=2ⁿ

Примеры:

1. 0,00110₂-A₈=0,14₈

001 100₂ =14₈

2. 0,00110₂-A₁₆0,30₁₆

0011 0000₂=30₁₆

Перевод произвольных чисел

Для того, чтобы произвольное двоичное число записать в системе счисления с основанием q=2ⁿ (4, 8, 16, и т. д.) нужно:

1. разбить данное число на целую и дробную части и применить соответствующие алгоритмы

Пример:

110111100111001, 00110₂-A₈=67471,14₈

110 111 100 111 001₂=67471₈

001 100₂ =14₈

Для того, чтобы произвольное число, записанное в системе счисления с основанием q=2ⁿ , перевести в двоичную систему счисления, нужно каждую цифру этого числа заменить ее n – разрядным эквивалентом в двоичной системе счисления

Пример:

15FC₁₆=0001 0101 1111 1100₂

Двоичная арифметика

+ 0 1 0 0 1 1 1 10

- 0 1 0 0 11 1 1 0

* 0 1 0 0 0 1 0 1

Примеры:

1001+1010 1 0 0 1 + 1 0 1 0 1 0 0 1 1	1. 1011-111 1 0 1 1 - 1 1 1 1 0 0	1.1011*111 1 0 1 1 * 1 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 0 1 1 0 1
1111+1 1 1 1 1 + 1 1 0 0 0 0	2.1100,0-10,1 1 1 0 0, 0 - 1 0, 1 1 0 0 1, 1
101,011+1,11 1 0 1, 0 1 1 + 1, 1 1 1 1 1, 0 0 1	3.11-1011=-(1011-11) 1 0 1 1 - 1 1 1 0 0 0

Решение задач по теме «Системы счислений»

1. Сравните числа

1). 5₁₀ и 5₈

Решение

В системе счисления с основанием 10 используются 10 цифр 0,1,2,3,4,5,6,7,8,9

В системе счисления с основанием 8 используются 8 цифр 0,1,2,3,4,5,6,7

Ответ: 5₁₀₌5₈

2). 1111₂ и 1111₈

Решение

Переведем 1111₂ в восьмеричную систему

001 111 =17₈

17₈₈

Ответ: 1111_{2 8}

2.В коробке лежит 31₈ шар. Среди них 12₈ красных и 17₈ желтых. Докажите, что здесь нет ошибки

Решение

12₈=1*8¹+2*8⁰=8+2=10

17₈=1*8¹+7*8⁰=8+7=15

31₈=3*8¹+1*8⁰=3*8+1=25

Ответ: Ошибки нет

1. В классе 1111₂ девочек и 1010₂ мальчиков. Сколько учеников в классе.

Решение

1111₂=1*2³+1*2²+1*2¹+1*2⁰=8+4+2+1=15 девочек

1010₂=1*2³+0*2²+1*2¹+0*2⁰=8+2=10 мальчиков

15+10=25

Ответ: 25

1. Переведите число 2004₁₀ в двоичную систему и восьмеричную систему.

Решение

2004	2
2004	1002	2
0	1002	501	2
0		500	250	2
1			250	125	2
			0	124	62	2
				1	62	31	2
0						30	15	2
1							14	7	2
1								6	3	2
1									2	1
1

2004	8
2000	250	8
5	248	31	8
	2	24	3
		7

11111010100₂

3724₈

Ответ: 11111010100₂, 3724₈

1. Перевести числа в троичную и пятеричную системы счисления, оставив 4 знака после запятой: 30,5

Решение

30 3 30 10 3 0 9 3 3 1 3 1 0

0 5 * 3 1 5 * 3 1 5 * 3 1 5 * 3 1 5

30 5 30 6 5 0 5 1 1

0 5 * 5 2 5 * 5 2 5 * 5 2 5 * 5 2 5

Ответ: 101,1111₃ 110,2222₅

1. Сколько единиц в двоичной записи десятичного числа 194,5?

Решение

194 2 194 97 2 0 96 48 2 1 48 24 2 0 24 12 2 0 12 6 2 0 6 3 2 0 2 1 1

0 5 * 2 1 0

194,5₁₀=11000010,1₂

Ответ: 4 единицы

1. Вычислите сумму чисел x и y, при x=A6₁₆, y=75₈.

Решение

A6₁₆=1010 0110

75₈=111 101

1	0	1	0	0	1	1	0
+		1	1	1	1	0	1
1	1	1	0	0	0	1	1

Ответ: 11100011₂

1. Для кодирования букв A, Б, В, Г решили использовать двухразрядные двоичные числа (от 00 до 11 символов соответствен). Если таким образом закодировать последовательность символов Г, Б, А, В и записать результат шестнадцатеричным кодом, то получится:

Решение

А 00 Б 01 В 10 Г 11

ГБВА=1101 0010₂=D2₁₆

Ответ: D2₁₆

1. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 1.

Решение

23-1=22

Делителями числа 22 являются

2,11,22

Ответ: 2,11,22

10. Дано а=D7₁₆, b=331₈. Какое из чисел c, записанных в двоичной системе, отвечает условию a

1)

11011001

2)

11011100

3)

11010111

4)

11011000

Решение

Переводим числа в одну систему счисления, например, в двоичную:

a=1101 0111₂ b=1101 1001₂

Варианты ответов 1) и 3) совпадают с числами a и b. Следовательно, эти варианты не подходят, так как стоит строгое неравенство. Видно также, что во всех предлагаемых числах старшие 4 бита одинаковы. Можно их в дальнейшем не рассматривать.

Поучаем для варианта ответа 2) и 4) 0111

Ответ: х=1000

1. В системе счисления с некоторым основанием число 19 записывается в виде 201. Укажите это основание.

Решение

Основание 2 не подходит т. к в двоичной системе могут быть только цифры 0 и 1

19 3 18 6 3 1 6 2 0 Основание равно 3

Ответ: 3

1. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием четыре оканчивается на 11.

Решение

25	4
24	6	4
1	4	1
	2

В системе счисления с основанием 4 может быть только 3 разряда = числа могут быть представлены как х11, где х=0 или 1 (2 и 3 не подходят, т. к. по условию задачи х11₄121₄)

011 или 111

011₄=0*4²+1*4¹+1*4⁰=4+1=5

111₄=1*4²+1*4¹+1*4⁰=16+4+1=14

Ответ: 5, 14

Тема 2. Основы логики

Пусть даны 2 высказывания А и В, из них можно составить новые составные высказывания используя связки «и», «или», «не» и т. д.

Определение 1. Два составных высказывания называются равносильными (эквивалентными) если они одновременно истинны и одновременно ложны

АВ

Определение2. Отрицанием высказывания А называется высказывание А истинное тогда и только тогда, когда А – ложное

1). Пусть А простое число 5

А «5-простое число»

А «5 – непростое число»

2). Дано высказывание 3² больше 6

В «3² больше 6»

В «3²меньше 6»

Таблица истинности для отрицания (инверсия)

А	И	Л
А	Л	И

АА

Определение 3. Пусть даны два высказывания А и В. Конъюнкцией двух высказываний А и В, называется новое составное высказывание АВ истинное тогда и только тогда, когда оба высказывания истинны. Образуется в речи с помощью союза «И»

Таблица истинности для конъюнкции

А	И	И	Л	Л
В	И	Л	И	Л
АВ	И	Л	Л	Л

А «10/2» И

В «10/5» И

АВ «10/2» «10/5» И

Определение 4.

Дизъюнкцией двух высказываний называется новое составное высказывание АВ ложное тогда и только тогда, когда оба высказывания ложные. Образуется в речи с помощью союза «ИЛИ»

Таблица истинности для дизъюнкции

А	Л	И	Л	И
В	Л	И	И	Л
АВ	Л	И	И	И

А «73» И

В «10=7» Л

АВ= «73» «10=7» И

Определение 5. Импликацией двух высказываний А и В называется высказывание АВ ложное тогда и только тогда, когда высказывание А – истинно, а В – ложно

Таблица истинности для импликации

А	И	И	Л	Л
В	Л	И	И	Л
АВ	Л	И	И	И

Ложь =0

Истинна=1

Таблицы истинности

конъюнкции	дизъюнкции	импликации	инверсия
А И И Л Л В И Л И Л АВ И Л Л Л	А Л И Л И В Л И И Л АВ Л И И И	А И И Л Л В Л И И Л АВ Л И И И	А И Л А Л И
А 1 1 0 0 В 1 0 1 0 АВ 1 0 0 0	А 0 1 0 1 В 0 1 1 0 АВ 0 1 1 1	А 1 1 0 0 В 0 1 1 0 АВ 0 1 1 1	А 1 0 А 0 1

Основные законы логики

Название закона	Формулировка
Переместительный
Сочетательный
Распределительный
Закон непротиворечий
Закон исключенного третьего
Закон двойного отрицания
Законы де Моргана

Импликация через отрицание и логическое сложение

АВ=АВ

Свойства конъюнкции, дизъюнкции и импликации

А0=А

А0=0

А1=1

А1=А

0А=1

Решение задач по теме «Основы логики»

1. Для какого из указанных значений X истинно высказывание ¬ ((X2) – (X3))?

1)

1

2)

2

3)

3

4)

4

Решение:

В записи логического высказывания стоит отрицание сложного высказывания.

Если ((X 2) – (X 3)) = 1 (истинно), то (X 2) – (X 3) = 0 (ложно)

Импликация ложна в единственном случае, тогда (X 2) = 1, а (X 3) = 0.

Получаем, что X 2 и X ≤ 3. Только одно число входит в этот промежуток. Это 3.

Ответ: 3.

2. Для какого из указанных значений числа X истинно высказывание

((X 3) – (X 4))

1)

1

2)

2

3)

3

4)

4

Решение:

В записи логического высказывания стоит отрицание сложного высказывания.

Если ((X 3) – (X 4)) = 1 (истинно), то (X 3) – (X 4) = 0 (ложно)

Импликация ложна в единственном случае, тогда (X 3) = 1, а (X 4) = 0.

Получаем, что X должно быть 3 и X ≤ 4. Только одно число входит в этот промежуток. Это 4.

Ответ: 4.

3. Для какого из указанных значений числа X истинно высказывание

((X  (X 2)) – (X 4)

1) 1 2) 2 3) 3 4) 4

Решение:

Cоставим таблицу истинности для указанных высказываний (1 – истина, 0 – ложь):

X	X	X2	(X  (X 2)	X4	((X  (X 2)) – (X 4)
1	1	0	1	0	0
2	0	0	0	0	1
3	0	1	1	0	0
4	0	1	1	0	0

Ответ: 2.

4. Укажите, какое логическое выражение равносильно выражению

A /\ ¬ (¬B \/ C).

1)	¬A \/ ¬B \/ ¬C
2)	A /\ ¬B /\ ¬C
3)	A /\ B /\ ¬C
4)	A /\ ¬B /\ C

Решение:

Перед скобкой стоит инверсия. Применяем закон де Моргана для дизъюнкции.

Получаем A /\ ¬ (¬B \/ C) = A /\ B /\ ¬ C.

Ответ: 3.

5. Укажите, какое логическое выражение равносильно выражению

¬A \/ ¬ (B \/ C)

1)

¬A \/  B \/ ¬C

2)

A  (B /\ C)

3)

A \/ B \/ C

4)

¬A  B /\ ¬C

Решение:

Перед скобкой стоит инверсия. Применяем закон де Моргана для дизъюнкции.

Получаем ¬A \/ ¬ (B \/ C) = ¬A \/ ¬ B /\ ¬ C.

Ответ: 4.

6. Укажите, какое логическое выражение равносильно выражению

¬(A \/ B) \/ C

1) (A  B) \/ ¬C 2) A  ¬B C 3) ¬A \/ B \/ ¬C 4) (¬A /\ B)  ¬C

Решение:

Перед скобкой стоит инверсия. Применяем закон де Моргана для дизъюнкции.

Получаем ¬ ¬A /\ ¬B \/ ¬C = A /\ ¬ B \/ ¬C.

Ответ: 1.

7. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов X, Y, Z.

Дан фрагмент таблицы истинности выражения F:

X	Y	Z	F
0	1	0	0
0	1	1	1
1	1	0	0

Какое выражение соответствует F?

1)	X \/ ¬Y \/ Z
2)	X /\ Y /\ Z
3)	X /\ Y /\ Z
4)	¬X \/ Y \/ ¬Z

Решение:

Составим таблицы истинности для каждого из четырёх выражений:

X	Y	Z	¬X	Y	Z	1) X \/ ¬Y \/ Z	2)X /\ Y /\ Z	3) X /\ Y /\ Z	4) ¬X \/ Y \/ ¬Z
0	1	0	1	0	1	1	0	0	1
0	1	1	1	0	0	1	0	1	1
1	1	0	0	0	1	1	1	0	1

Искомому значению F соответствует 3) вариант ответа.

Ответ: 3.

8. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.

Дан фрагмент таблицы истинности выражения F:

X	Y	Z	F
1	0	0	1
0	0	0	1
1	1	1	0

Какое выражение соответствует F?

1)

¬X /\ ¬Y /\ ¬Z

2)

X /\ Y /\ Z

3)

X \/ Y \/ Z

4)

¬X \/ ¬Y \/ ¬Z

Решение:

Составим таблицы истинности для каждого из четырёх выражений:

X	Y	Z	¬X	Y	Z	1) X /\ Y /\ Z	2) X /\ Y /\ Z	3) X \/ Y \/ Z	4) ¬X \/ ¬Y \/ ¬Z
1	0	0	0	1	1	0	0	1	1
0	0	0	1	1	1	1	0	0	1
1	1	1	0	0	0	0	1	1	0

Искомому значению F соответствует 4) вариант ответа.

 Ответ: 4.

9. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов X, Y, Z.

Дан фрагмент таблицы истинности выражения F:

X	Y	Z	F
0	1	0	0
1	1	0	1
1	1	1	1

Какое выражение соответствует F?

1) X \/ Y \/ Z 2) X /\ Y /\ Z 3) X /\ Y /\ Z 4) X \/ Y \/ Z

Решение:

Составим таблицы истинности для каждого из четырёх выражений:

X	Y	Z	¬X	Y	Z	1) X \/ Y \/ Z	2) X /\ Y /\ Z	3) X /\ Y /\ Z	4) X \/ Y \/ Z
0	1	0	1	0	1	1	0	0	0
1	1	0	0	0	1	1	0	0	1
1	1	1	0	0	0	1	0	0	1

Искомому значению F соответствует 4) вариант ответа.

Ответ: 4.

10. Каково наибольшее целое число X, при котором истинно высказывание

(50 (50(X+1) ·(X+1))?

Решение:

(50²) – (50(X+1)²)

В выражении (50 (50(X+1) ·(X+1)) между скобками стоит импликация, которая истинна в трех случаях: когда условие (первое выражение) ложно и следствие (второе выражение) – ложно); когда оба выражения истинны и когда первое выражение ложно, а второе - истинно.

Рассмотрим ситуацию, когда оба выражения ложны.

(50²) = 0 → 50=X². Эта ситуация возможна только при максимальном Х=7

50(X+1)² = 0 → 50². 50². 50

Ответ: 7.

11. Дано логическое выражение (ML)(KLN). Укажите значения переменных K, L, M, N, при которых логическое выражение ложно.

Ответ запишите в виде строки из четырех символов – значений переменных K, L, M и N (в указанном порядке). Так, например, строка 0101 соответствует тому, что K=0, L=1, M=0 и N=1.

Решение:

В выражении (ML)(KLN) между скобками стоит импликация, которая ложна только в единственном случае: когда условие (первое выражение) истинно, а следствие (второе выражение) – ложно).

Рассмотрим следствие: (KLN)=0. Дизъюнкция ложна, когда все слагаемые ложны, то есть K=0, L=0, N=0. Следовательно, K=0, L=1, N=1.

Теперь рассматриваем условие: (ML)=1. Подставляем е выражение найденное значение L.

(M1)=1

(M0)=1

Истина возможна только при M=1. Получаем итоговый результат: K=0, L=1, M=1, N=1.

Ответ: 0111

12. Сколько различных решений имеет уравнение

JKLM(NN)=0

где J, K, L, M, N – логические переменные?

В ответе не нужно перечислять все различные наборы значений J, K, L, M и N, при которых выполнено данное равенство. В качестве ответа Вам нужно указать количество таких наборов.

Решение:

Можно строить таблицу истинности, а можно рассуждать логически на основании принципа построения таблицы истинности. В уравнении 5 переменных, значит всего наборов в таблице истинности 2⁵ = 32. Необходимо определить, на каких наборах из 32 уравнение равно 0.

1) Уравнение можно упростить: по законам алгебры логики NN = 1

JKLM1 = JKLM

JKLM=0

Уравнение ложно тогда, когда ложно хотя бы одно из входящих в его состав высказываний.

2) Высказывание J стоит первым в таблице истинности, значит, оно имеет 16 наборов 0, потому что строки таблицы истинности для первого столбца делятся пополам и верхняя половина заполняется 0, нижняя 1. В дальнейших рассуждениях эти наборы не рассматриваем.

3) Высказывание К стоит вторым в таблице истинности. Значит, 32 делим на 4. То есть высказывание K на 8 наборах из оставшихся 16 равно 0. Остается 8 наборов, на которых K=1.

4) Рассуждая подобным образом, делим для высказывания L, которое стоит третьим в таблице истинности, 32 на 8. Значит, L будет равно 0 в 4 случаях из оставшихся 8-ми наборов.

5) Остается 4 набора. Для выражения M, которое стоит в таблице истинности в четвертом столбце, 32: 16 = 2, то есть на двух наборах из оставшихся 4-х это выражение равно 0.

6) Суммируем все наборы 16+8+4+2=30

Ответ: 30.