ТЕОРЕМЫ ОБ УГЛАХ,
ОБРАЗОВАННЫХ ДВУМЯ
ПАРАЛЛЕЛЬНЫМИ
ПРЯМЫМИ
И СЕКУЩЕЙ
22 ЯНВАРЯ 2010Г
Учитель Козина Н.А.
ПОНЯТИЕ ОБРАТНОЙ ТЕОРЕМЫ
ЕСЛИ
Условие
Заключение
ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ СЕКУЩЕЙ НАКРЕСТ ЛЕЖАЩИЕ УГЛЫ РАВНЫ,
ТО
ПРЯМЫЕ ПАРАЛЛЕЛЬНЫ
ТЕОРЕМа
Свойство
накрест лежащих углов
ЕСЛИ ДВЕ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ ПЕРЕСЕЧЕНЫ СЕКУЩЕЙ,
ТО НАКРЕСТ ЛЕЖАЩИЕ УГЛЫ РАВНЫ.
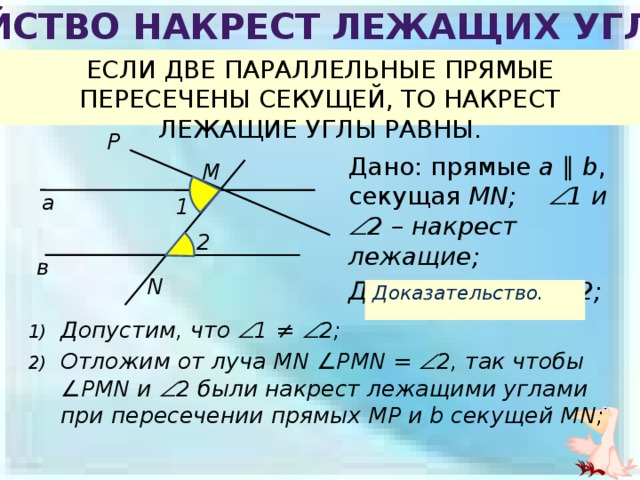
Свойство накрест лежащих углов
ЕСЛИ ДВЕ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ ПЕРЕСЕЧЕНЫ СЕКУЩЕЙ, ТО НАКРЕСТ ЛЕЖАЩИЕ УГЛЫ РАВНЫ.
P
Дано: прямые a ∥ b , секущая MN; 1 и 2 – накрест лежащие;
Доказать: 1 = 2;
M
а
1
2
в
N
Доказательство.
- Допустим, что 1 ≠ 2;
- Отложим от луча MN ∠PMN = 2, так чтобы ∠PMN и 2 были накрест лежащими углами при пересечении прямых MP и b секущей MN;
P
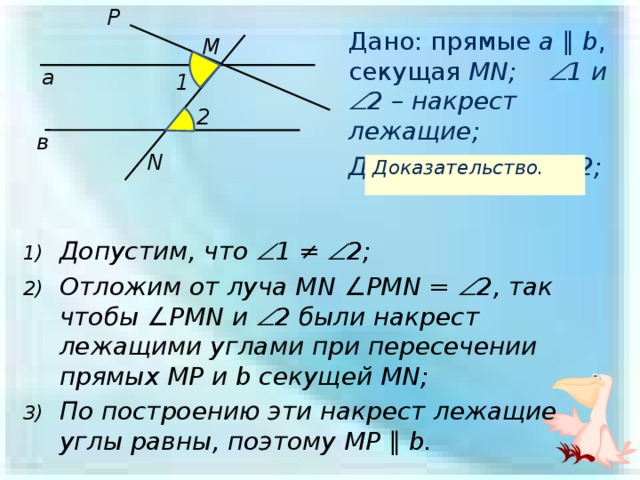
Дано: прямые a ∥ b , секущая MN; 1 и 2 – накрест лежащие;
Доказать: 1 = 2;
M
а
1
2
в
N
Доказательство.
- Допустим, что 1 ≠ 2;
- Отложим от луча MN ∠PMN = 2, так чтобы ∠PMN и 2 были накрест лежащими углами при пересечении прямых MP и b секущей MN;
- По построению эти накрест лежащие углы равны, поэтому MP ∥ b.
P
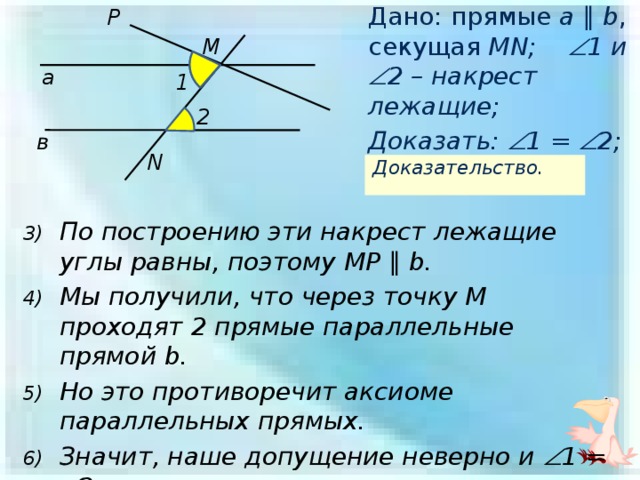
Дано: прямые a ∥ b , секущая MN; 1 и 2 – накрест лежащие;
Доказать: 1 = 2;
M
а
1
2
в
N
Доказательство.
- По построению эти накрест лежащие углы равны, поэтому MP ∥ b.
- Мы получили, что через точку М проходят 2 прямые параллельные прямой b.
- Но это противоречит аксиоме параллельных прямых.
- Значит, наше допущение неверно и 1 = 2;
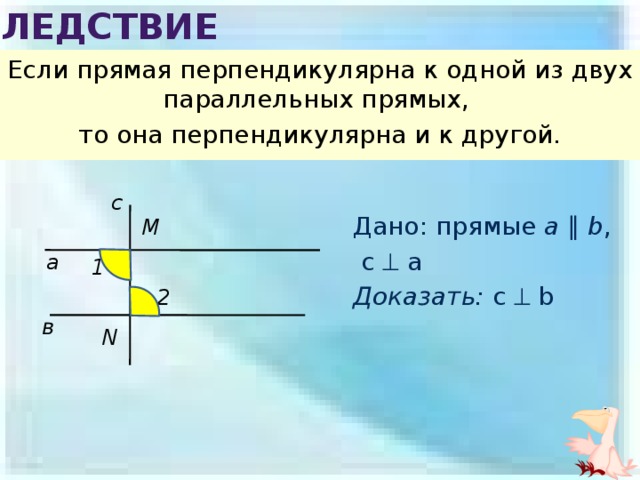
следствие
Если прямая перпендикулярна к одной из двух параллельных прямых,
то она перпендикулярна и к другой.
с
Дано: прямые a ∥ b ,
M
c a
Доказать: c b
а
1
2
в
N
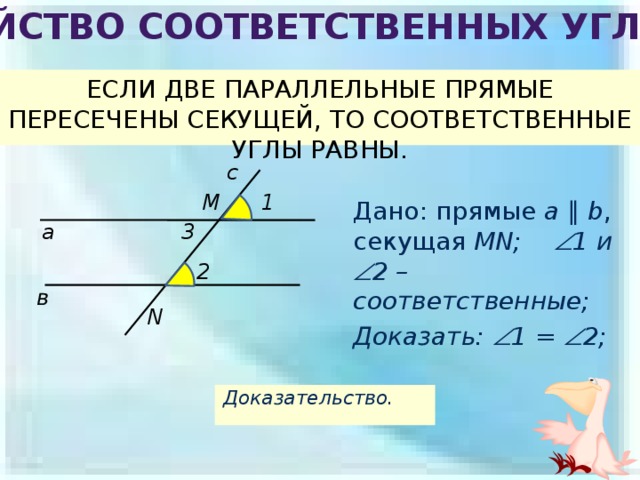
Свойство соответственных углов
ЕСЛИ ДВЕ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ ПЕРЕСЕЧЕНЫ СЕКУЩЕЙ, ТО СООТВЕТСТВЕННЫЕ УГЛЫ РАВНЫ.
с
1
M
Дано: прямые a ∥ b , секущая MN; 1 и 2 – соответственные;
Доказать: 1 = 2;
а
3
2
в
N
Доказательство.
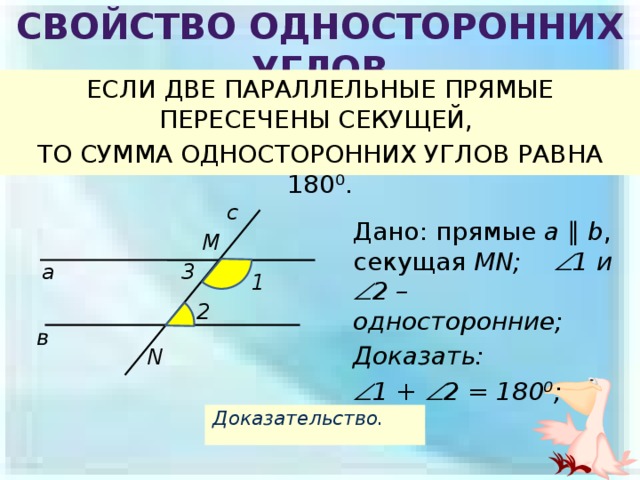
Свойство односторонних углов
ЕСЛИ ДВЕ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ ПЕРЕСЕЧЕНЫ СЕКУЩЕЙ,
ТО СУММА ОДНОСТОРОННИХ УГЛОВ РАВНА 180⁰.
с
Дано: прямые a ∥ b , секущая MN; 1 и 2 –односторонние;
Доказать:
1 + 2 = 180⁰;
M
а
3
1
2
в
N
Доказательство.
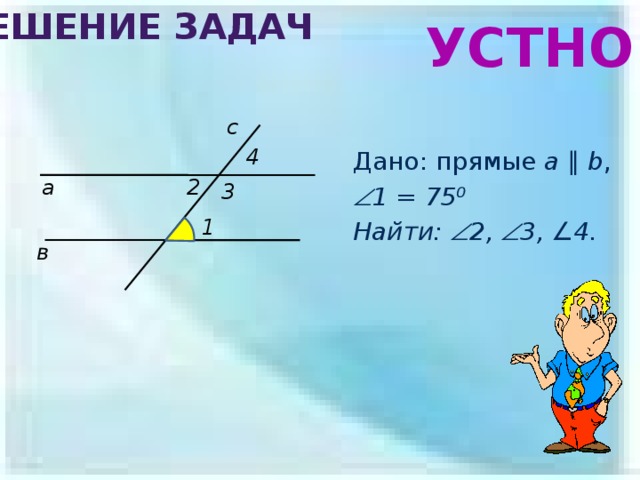
Решение задач
УСТНО
с
4
Дано: прямые a ∥ b ,
1 = 75⁰
Найти: 2, 3, ∠4 .
а
2
3
1
в
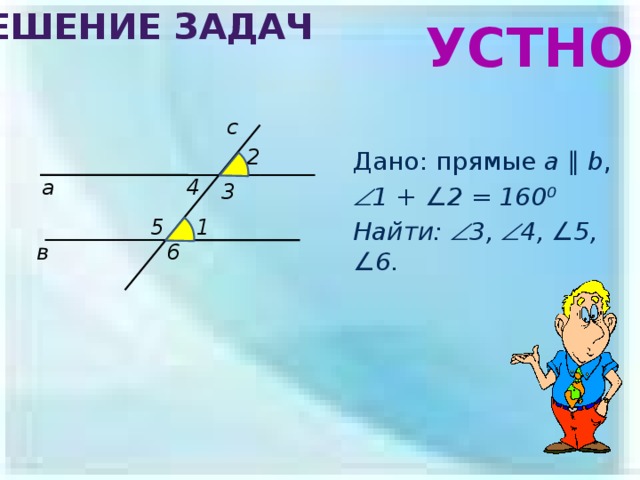
Решение задач
УСТНО
с
2
Дано: прямые a ∥ b ,
1 + ∠2 = 160⁰
Найти: 3, 4, ∠5 , ∠6.
а
4
3
5
1
в
6
РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА
ПАРАЛЛЕЛЬНЫХ
ПРЯМЫХ»
- 26 ЯНВАРЯ 2010Г
- Учитель Козина Н.А.
РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ»
УСТНО
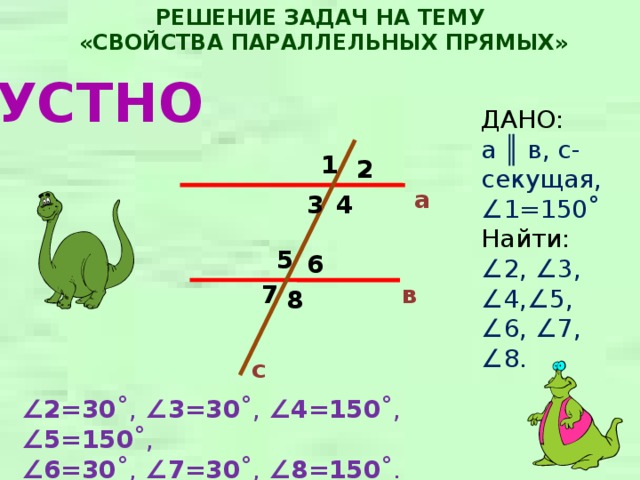
ДАНО:
а ║ в, с-секущая, ∠ 1=150˚
Найти:
∠ 2, ∠ 3, ∠ 4, ∠ 5, ∠ 6, ∠ 7, ∠ 8.
1
2
а
3
4
5
6
в
7
8
с
∠ 2=30 ˚, ∠ 3=30 ˚, ∠ 4=150 ˚, ∠ 5=150 ˚,
∠ 6=30 ˚, ∠ 7=30 ˚, ∠8 =150 ˚.
РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ»
УСТНО
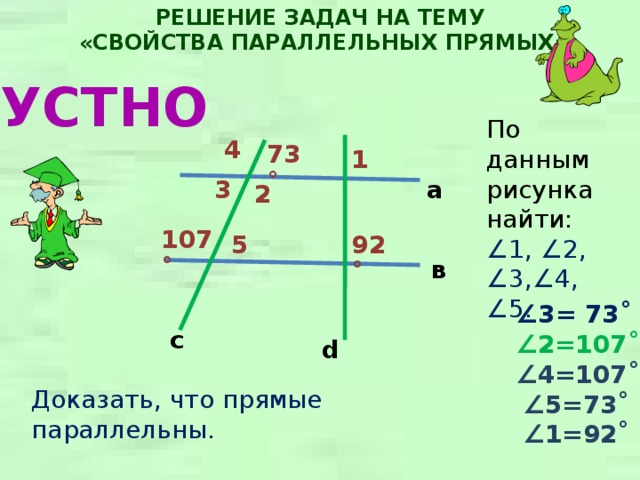
По данным рисунка найти:
∠ 1, ∠ 2, ∠ 3, ∠ 4, ∠ 5.
4
73˚
1
3
а
2
107˚
92˚
5
в
∠ 3= 73˚
с
∠ 2=107˚
d
∠ 4=107˚
Доказать, что прямые параллельны.
∠ 5=73˚
∠ 1=92˚
РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ»
№ 1
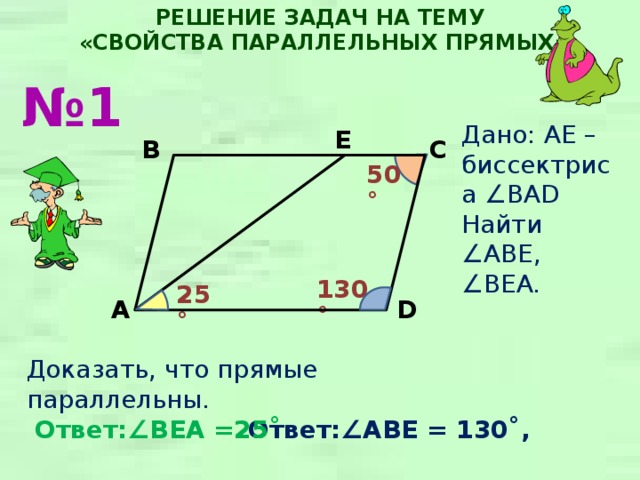
Дано: AE – биссектриса ∠BAD
Найти
∠ ABE, ∠BEA.
E
C
B
50˚
130˚
25˚
A
D
Доказать, что прямые параллельны.
Ответ:∠ BEA =25˚
Ответ:∠ ABE = 130˚,
РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ»
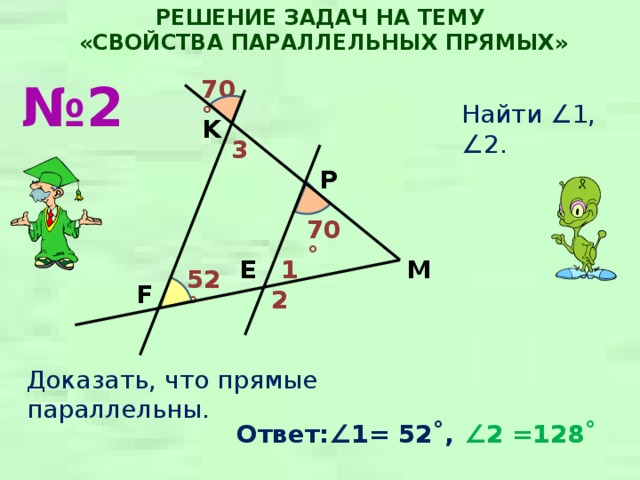
№ 2
70˚
Найти ∠1, ∠2.
K
3
P
70˚
E
M
1
52˚
F
2
Доказать, что прямые параллельны.
∠ 2 =128˚
Ответ:∠ 1= 52˚,
РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ»
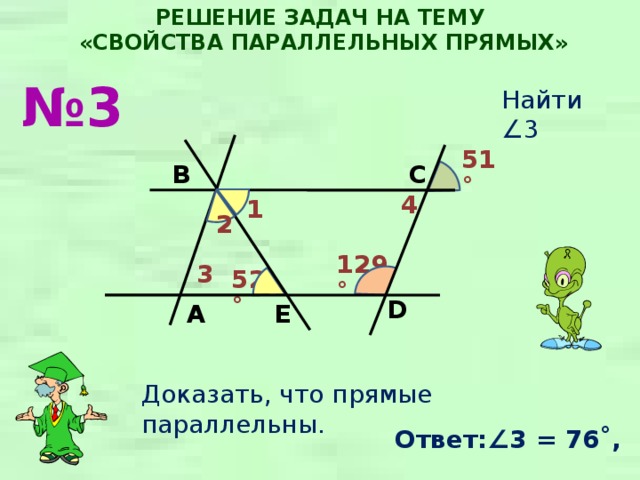
№ 3
Найти ∠3
51˚
C
B
4
1
2
129˚
3
52˚
D
E
A
Доказать, что прямые параллельны.
Ответ:∠ 3 = 76˚,
РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ»
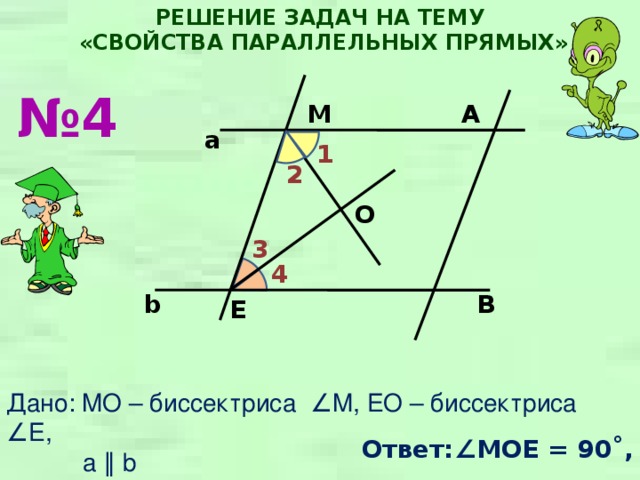
№ 4
A
M
a
1
2
O
3
4
B
b
E
Дано: MO – биссектриса ∠M, EO – биссектриса ∠E,
a ∥ b
Найти ∠MOE
Ответ:∠ MOE = 90˚,
РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ»
САМОСТОЯТЕЛЬНО
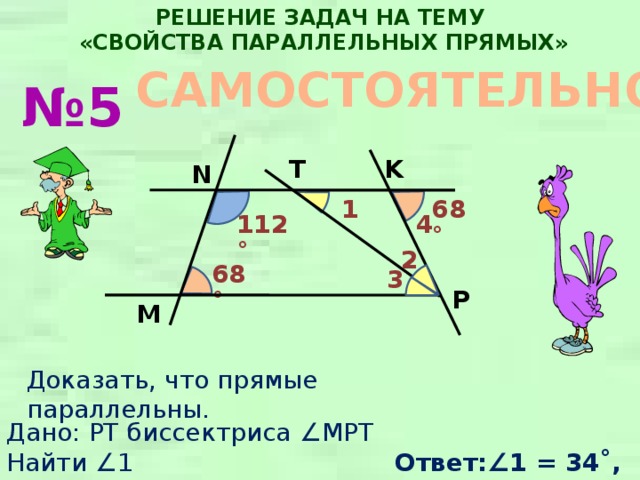
№ 5
T
K
N
68˚
1
112˚
4
2
68˚
3
P
M
Доказать, что прямые параллельны.
Дано: PT биссектриса ∠MPT
Найти ∠1
Ответ:∠ 1 = 34˚,
РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ»
ДОМАШНЕЕ ЗАДАНИЕ
№ 208, 210, 211, 212
Получите свидетельство
Вход
Свойства углов при параллельных прямых (0.23 MB)
2
8440
500
Нравится
0
