Статья на тему: "Развитие креативных способностей учащихся на уроках математики"

Аннотация. 

В статье рассматривается описание креативного урока по системе непрерывного формирования универсальных учебных действий на уроках

математики. Представлена разработка креативного урока в соответствии со

структурой креативного урока в инновационной педагогической системе НФТМ -

ТРИЗ разработаны все блоки урока. Рассматривается решение практических и

творческих задач в соответствии с выбранной темой.

Ключевые слова: универсальные учебные действия, творческие задания, развитие творческих способностей, формирования креативной компетентности учащегося.

Текстовые задачи играют важную роль в процессе обучения математике в школе. Они позволяют проверить не только владение определенными математическими операциями, но и умение анализировать, рассуждать, делать выводы, проверять правильность полученного результата, применять знания в нестандартной ситуации, т. е. развивают логику мышления.

Задачи являются материалом для ознакомления учащихся с новыми понятиями, для развития логического мышления, формирования межпредметных связей. Задачи позволяют применять знания, полученные при изучении математики, при решении вопросов, которые возникают в жизни человека. Этапы решения задач являются формами развития мыслительной деятельности. Велика роль задач в развитии мышления и в математическом воспитании учащихся, в формировании у них умений и навыков в практических применениях математики.

Обобщающий урок представляет собой разработку спаренных уроков по алгебре в 9 - м классе по теме «Решение текстовых задач». Данные уроки могут быть проведены как с целью повторения решения текстовых задач по всему курсу основной средней школы, так и для подготовки обучающихся к сдаче экзаменов в 9 - х классах при тематическом повторении.

Разработка урока в 9 классе по теме «Решение текстовых задач».

Цели урока:

дидактические:

• повторение, обобщение, систематизация знаний;
• проверка уровня усвоения темы;
• развитие у учащихся интереса к предмету через решение прикладных задач и умения применить математические знания в практической деятельности.

психологические:

• формирование и дальнейшее развитие познавательных операций по планированию и прогнозированию учебной деятельности;

воспитательные:

• формирование логического, системного мышления;
• развитие интеллектуальных умений и мыслительных операций − анализ и синтез, сравнение, обобщение.

Тип урока: обобщение и систематизация знаний.

Оборудование: компьютер, мультимедийный проектор, интерактивная доска.

Ход урока.

«Что значит владение математикой?

Это есть умение решать задачи, причем не только стандартные, но и требующие известной независимости мышления, здравого смысла , оригинальности , изобретательности. »

Д. Пойа.

1. Мотивация.

На сегодняшнем уроке мы продолжим разговор о текстовых задачах.

Задача 1.

В клетке находится неизвестное число фазанов и кроликов. Известно, что вся клетка содержит 35 голов и 94 ноги. Узнать число фазанов и число кроликов. Кто хочет поразмыслить по поводу этой задачи? Ведь это всем известная задача.

Задача 2

Мама раздала детям по четыре конфеты, и три конфеты остались лишними. А чтобы дать детям по пять конфет, двух конфет не хватает. Сколько было детей?

Кто хочет поразмыслить по поводу этой задачи?

Задача 3

Может ли такое быть? Одного человека спросили:

• Сколько вам лет?
• Порядочно, – ответил он.
• Я старше некоторых своих родственников почти в шестьсот раз. Может ли такое быть? Может, например если человеку 50 лет, а его внуку или внучке 1 месяц.

2. Содержательная часть [1].

Ответьте на вопросы:

• Какую формулу следует применить при решении задач на движение? Что в данной формуле обозначают буквы S, t, v?
• Какие величины используют при решении задач на работу? Как можно задать формулу работы?
• Что такое производительность труда и можно ли ее сравнить со скоростью движения?

ЗАДАЧИ НА ДВИЖЕНИЕ

Уравнения, которые составляются на основании условий задач на движение, обычно содержат такие величины, как расстояние, скорости движущихся объектов, время, а также скорость течения воды (при движении по реке).

Задача 1. Пароход прошел 4 км против течения реки, а затем прошел еще 33 км по течению, затратив на весь путь один час. Найдите собственную скорость парохода, если скорость течения реки равна 6, 5 км/ч [2].

Решение:

Смотрите документ

 Ответ: v=32, 5 км/ч.

Задача 2. В заезде на одну и ту же дистанцию участвовали два автомобиля и мотоцикл. Второму автомобилю на всю дистанцию потребовалось на 1 мин больше, чем первому. Первый автомобиль двигался в 4 раза быстрее мотоцикла. Какую часть дистанции в минуту проходил второй автомобиль, если он проходил в минуту на 1/6 дистанции больше, чем мотоцикл, а мотоцикл прошел дистанцию меньше, чем за 10 мин?

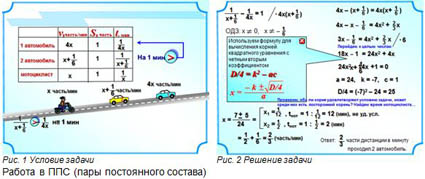
Весь материал – смотрите документ.