
 Из опыта работы
Из опыта работы
учителя математики
МКОУ Костромского муниципального района Костромской области «Никольская средняя общеобразовательная школа"
Кузьминой Евгении Александровны
Подготовка учащихся
к итоговой аттестации
за курс средней школы


2015 год
Подготовка к ЕГЭ начинается с 5 класса. Одной из основных задач преподавания математики является формирование у учащихся сознательных и прочных вычислительных навыков. Для этого учителя пользуются различными методическими приёмами.
У учащихся с прочными вычислительными навыками (вычислительные навыки отличаются от умений тем, что выполняются почти бесконтрольно) гораздо меньше проблем с математикой. Но чтобы ученик быстро считал, выполнял простейшие алгебраические преобразования, необходимо время для их отработки. Это должно быть в системе.
Для обработки и закрепления вычислительных навыков я применяю карточки устного счёта, которые я позаимствовала в журнале «Математика в школе» №5 за 1995г. Эти карточки размножаются на каждого ученика и даже могут быть выданы домой для тренировки. Полезный материал для отработки вычислительных навыков можно взять в книге «Дидактические игры на уроках математики» автор В.Г. Коваленко. Это «Числовая мельница», «Числовой фейерверк» и многое другое.
Хороший тренировочный материал имеется в учебнике математики 5-6 классы Н.Я. Виленкина. Это задания цепочки:
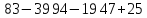
:4 :25 :18
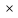 7
7 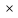 15
15 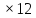
+23 +55 -19
? ? ?
Можно использовать рабочую тетрадь по математике для 5-6 классов автор З.Н. Альхова (тетрадь в двух частях). Издательство «Лицей» 2001г. (образцы прилагаются). В учебнике «Алгебра 7-11 классы» А.Д. Мордковича. Здесь очень много устных упражнений, которые учитель может использовать для устного тренажа.
Очень важное значение при изучении любого предмета играет УМК, по которому идёт обучение.
На мой взгляд наиболее полный УМК под редакцией А.Г. Мордковича.
Что входит в УМК:
-учебник;
-задачник;
-контрольные работы под редакцией А.Г. Мордковича, Е.Е. Тульчинской;
-самостоятельные работы под редакцией Л.А. Александровой;
-тематические тексты и зачеты под редакцией Л.О. Денищевой;
-для 7-9 классов рабочая тетрадь под редакцией М.Б. Волович;
-методическое пособие для учителя под редакцией А.Г. Мордковича.
Важную роль в работе учителя играют формы проверки состояния обученности учащихся. Я использую традиционные формы проверки: самостоятельные работы, контрольные работы, зачёты. К нетрадиционным формам проверки состояния обученности можно отнести тестирование.
Предлагаемые самостоятельные работы использую для текущего контроля знаний, умений и навыков учащихся по определённой теме. Время, отводимое на самостоятельные работы, варьируется от 7 до 20 минут в зависимости от структуры урока, объёма и сложности работы, уровня подготовки учащихся. Работы представлены в четырёх вариантах. Задания каждого варианта подобраны по возрастанию сложности, причём варианты 1 и 2 во многих случаях несколько легче вариантов 3 и 4 (т. е. дифференцированный подход здесь уже заложен автором).
Контрольные работы представлены в четырёх вариантах. В содержание работы входят задания базового уровня (до первой черты), среднего уровня (конструктивного уровня) - (от первой до второй черты) и задания повышенного уровня сложности (после второй черты). Все варианты по степени сложности равносильны.
Тематические тесты также представлены в четырёх вариантах. Тесты состоят из двух частей (1 часть - задания обязательного уровня, 2 часть - задания конструктивного и повышенного уровня). Тесты проводились на факультативах, оценка ставилась по желанию. Затем проводилась индивидуальная коррекция знаний учащихся.
Тематические зачёты составлены по каждой главе учебника и имеют двухуровневую структуру (обязательная часть и задания повышенной сложности). Предлагать одному и тому же ученику по одной теме в одно и то же время и тест и зачёт нецелесообразно. Поэтому я подходила индивидуально к каждому ученику. Те ученики, которые испытывают трудности в оформлении решений, записи обоснований, выполняют тест; другие учащиеся зачёт.
Для эффективной работы на каждого ученика имеется контрольный пакет, в котором имеется одного варианта контрольные работы и тесты.
После каждой контрольной работы обязательно провожу урок коррекции знаний. На уроке отвожу время индивидуальной работе с каждым учащимся. Каждый год веду тематический контроль ЗУН учащихся. Каждый ученик отчитывается за ошибки индивидуально, если не успевает на уроке, то приходит после уроков. Такая работа позволяет ликвидировать пробелы в знаниях учащихся по данной теме. (Такая тетрадь прилагается).
Организация повторения и подготовка к ЕГЭ идёт в 11 классе.
Тему «Понятие об определённом интеграле как площади криволинейной трапеции. Первообразная. Формула Ньютона-Лейбница. Примеры применения интеграла в физике и технике» изучаю в 10 классе.
В 11 классе изучаю темы: «Степени и корни. Степенные функции. Показательная и логарифмическая функции. Уравнения и неравенства». По тематическому планированию к марту месяцу данный материал должен быть изученным.
Повторение организую по основным линиям:
Рациональные выражения, уравнения , неравенства и функции.
Иррациональные выражения и уравнения. Функция
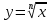 .
.Показательные уравнения, неравенства, системы и функции.
Логарифмические выражения, уравнения, неравенства и функции.
Тригонометрические выражения, уравнения, системы и функции.
Каждую тему повторяю по плану:
-тождественные преобразования выражений;
-решение уравнений, неравенств и их систем;
-исследование свойств функции.
При организации повторения обратить внимание на усвоение всеми учащимися теоретических вопросов, на отработку практических умений и навыков заданий обязательного и конструктивного уровня (учить учащихся размышлять и анализировать в изменённой незнакомой ситуации). Учить рациональным приёмам выполнения заданий части В, т.к. должен быть выигрыш во времени.
При повторении для контроля использую тематические тесты, составленные учителем по темам:
-преобразование тригонометрических выражений и тригонометрические уравнения;
-обратные тригонометрические функции;
-функции;
-производная и первообразная;
-показательная, логарифмические функции;
-корень n-ой степени, степень с рациональным показателем.
После каждого теста провожу обязательные уроки коррекции знаний.
Работаем обязательно с тестами из серии «ЕГЭ по математике». Эти тесты использую как обучающие и тренировочные, так и контролирующие. Желательно тесты – контроля проводить на спаренных уроках. Обязательное условие: все тесты, разобранные в классе, дома, тесты - контроля остаются у учащихся с решением. Каждый ученик накапливает себе папку - тестов, которая поможет ученику организовать (если есть желание у него) самостоятельное повторение. Я считаю, что такая работа наиболее эффективна.
Уроки повторения и систематизации знаний часто провожу в форме уроков – практикумов. Такие уроки способствуют прочному усвоению учебного материала. На таких уроках учащиеся самостоятельно упражняются в практическом применении усвоенных теоретических знаний и умений. Основным способом организации деятельности учащихся на практикумах является групповая форма работы. При этом каждая группа образована по «силам».
В ходе выполнения работы учащиеся показывают знания, умения и навыки самостоятельного выполнения упражнений (обязательного, конструктивного и повышенного уровня).
Урок был и остаётся самой распространённой формой обучения, однако его роль и место в организации образовательного процесса претерпевают изменения. Учителю предоставлено право самостоятельно выбирать как методы и средства, так и формы, ориентированные и на развивающее личность обучение.
Существуют различные подходы к выбору основных структурных элементов урока. Общая дидактическая структура урока характеризуется следующими компонентами:
-актуализацией прежних знаний и способов действий;
-формирование новых знаний и способов действий;
-их применением, т.е. формированием умений.
Актуализация наряду с воспроизведением ранее изученного предполагает установление преемственных связей прежних и новых знаний, применение прежних знаний в новых ситуациях, их углубление и т.д. Второй компонент общей дидактической структуры урока связан с раскрытием сущности новых понятий, усвоением новых знаний и способов учебной и умственной деятельности учащихся, формированием их убеждений. Формирование умений умений достигается применением новых знаний и способов действий, их обобщением и систематизацией, использованием на практике и т.д.
На практике чаще используются традиционные формы проведения уроков:
- урок ознакомления с новым материалом;
- урок закрепления изученного;
- урок применения знаний и умений;
- урок обобщения и систематизации знаний;
- урок проверки и коррекции знаний и умений.
Уроки применения знаний и умений, урок обобщения и систематизации знаний часто провожу в форме уроков – практикумов. Такие уроки способствуют прочному усвоению учебного материала.
На таких уроках учащиеся самостоятельно упражняются в практическом применении усвоенных теоретических знаний и умений. Основным способом организации деятельности учащихся на практикумах является групповая форма работы. При этом каждая группа образована по уровню обученности. В ходе выполнения работы учащиеся показывают знания, умения и навыки самостоятельного выполнения упражнений (обязательного, конструктивного и повышенного уровня).
Приложение
Тема урока: Решение уравнений (11 класс)
Тип урока: Урок-практикум
Цели урока:
Образовательные: Обобщить и систематизировать знания учащихся об общих методах решения уравнений.
Развивающие: учить общению друг с другом, учить анализировать, сравнивать, размышлять. Развивать навыки самоконтроля
Воспитательные: воспитывать волю и настойчивость для достижения конечных результатов при решении уравнений; прививать умение сотрудничества
Оборудование: карточки – задания
ХОД УРОКА
I Начало урока
II Актуализация знаний
Перечислите простейшие уравнения, которые были нами изучены.
1. Линейное уравнение ax+b=0
2.Квадратное уравнение ax2+bx+c=0
3. Степенное уравнение xn=a
4.Показательное уравнение
5.Логарифмическое уравнение logax=b
6. Тригонометрические уравнения sinx=a, cos x=a, tgx=a, ctgx=a
Основным шагом в решении уравнения является преобразование уравнения к одному из простейших уравнений.
Полностью алгоритмизировать процесс преобразования нельзя, однако полезно знать наиболее употребительные приемы, общие для всех типов уравнений.
Давайте вспомним данные методы решения уравнений:
1. Замена уравнения h(f(x)) = h(g(x)) уравнением f(x)=g(x) этот метод можно применять
- при решении показательных уравнений переходим от уравнений
af(x) = ag(x) (a0, a = 1) к уравнению f(x) = g(x)
при решении логарифмических уравнений переходим от уравнения logaf(x) = logag(x) к уравнению f(x)=g(x);
- при решении иррациональных уравнений переходим от уравнения …… к уравнению

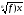 =
=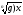
Акцентировать внимание учащихся на том, что этот метод применим только в том случае, когда функция y= h(x) – монотонная функция, которая каждое свое значение принимает по одному разу (либо функция возрастающая, либо убывающая на всей области определения)
2. Метод разложения на множители
уравнение f(x) g(x) h(x)=0 можно, заменить совокупностью уравнений f(x)=0, g(x)=0, h(x)=0
3. Метод введения новой переменной
- если уравнение f(x) =0 удалось преобразовать к виду p(g(x))=0 , то нужно ввести новую переменную t=g(x), решить уравнение p(x)=0, затем решить совокупность уравнений g(x)=t1 , g(x)=t2;…..; g(x)=tn где t1 , t2,……tn- корни уравнения p(t)=0
4. Функционально-графический метод
-для решения уравнения f(x)=g(x); нужно построить графики функций y=f(x), y=g(x) и найти точки их пересечения корнями уравнения служат абсциссы этих точек.
- если на промежутке X наибольшее значение одной из функций y=f(x), y=g(x) равно А и наименьшее значение другой функции тоже равно А, то уравнение f(x)=g(x) равносильно на промежутке X системе уравнений
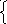
f(x)=А
g(x)=А
Задание: Выполните тест
Код ответов (1и2 группа)
№1 3
№2 2
№3 4
№4 4
Код ответов (3 группа)
№1 4
№2 2
№3 2
№4 4
III Основная часть урока
Практическая часть.
Сейчас мы переходим к выполнению практической работы. Вы будете решать уравнения, применяя изученные методы решения. Обратите внимание на грамотное решение на равносильные преобразования, на проверку корней, на возможность потери корня и как её не допустить, на рациональные приёмы решения
ТЕСТ (группа1 и 2)
1. Укажите промежуток, которому принадлежит корень уравнения
610x-1=36
1) (-4;-1) 3) (0;1)
2) [ -1;0) 4) [ 1;4)
2.Найдите сумму корней уравнения
lg(4x-3)=2 lgx
1) -2 3) -4
2) 4 4) 2
3) Решите уравнение
3cosx-sin2x=0
1) 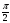 +2πk k
+2πk k

2) 2πk, k 

3) ± 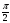 +
+ 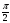
, k


4) 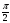 + πk, k
+ πk, k 

4. Решите уравнение
=
1) 1; 2
2) (0;1) и (0;2)
3) (1;1) и (4;2)
4) 1;4
Код ответов (1и2 группа)
№1 3
№2 2
№3 4
№4 4
ТЕСТ (3 группа)
1.Решите уравнение
tgx ·ctgx+cosx=0
1) 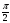 +πkk
+πkk 

2) 2 π k, k 

3) π +2πk, k

4) решений нет
2. Укажите промежуток, содержащий корень уравнения
3х+5=
1) (0;8) 3) (-15; -8)
2) (-8; 0) 4) (8; 10 )
3. Решите уравнение. Укажите корни уравнения. Если корней уравнения больше одного, то найдите сумму корней.
log2(x-6)= 0,5 log2x
1) 4 3)13
2) 9 4) решений нет
4. Сколько корней имеет уравнение
х3+5х-2=0
1) 3 3) нет решений
2) 2 4) 1
Код ответов (3 группа)
№1 4
№2 2
№3 2
№4 4
1 группа Карточка- помощник
№1 Решите уравнение
=х-1
(если уравнение имеет более одного корня, то в ответе укажите их произведение)
Решение
I способ:
=х-1
х-1
0, х
0
3х+10, х
-
Решаем уравнение
3х+1= (х-1)2 при условии, что х1
II способ:
Найдите корни уравнения и сделайте проверку, подставив в первоначальное уравнение
=х-1
№2 Найдите сумму корней уравнения 49·72х-50·7х+1=0
Решение
Введи новую переменную
t=7x , t0
49t2-50t=1=0
№3 Укажите число корней уравнения (х-6)·cosx=x-6
Решение
(х-6) ·cosx-(x-6)=0
вынеси общий множитель за скобки (х-6) · ( ) =0
№4 Решите уравнение
log0,3(7x+5) – log0,33=log0,34
Решение
log0,3(7x+5) – log0,33=log0,34
7x+50
x…
log0,3(7x+5) = log0,34+log0,33
примени свойство
log0,3(7x+5) = log0,3…
2 группа карточка – задание
№1 Решите уравнение
2-х=0
В ответе укажите разность между наибольшим и наименьшим корнем
Решение
2=х
(2 )3=х3
………………..
х+2-2х2-х3=0
Сгруппируй слагаемые
(х+2) + (-2х2-х3)=0
Вынеси общий множитель за скобки
№2 Найди произведение корней уравнения
log32 х –3 log22х=
Решение
ОДЗ х : х0
х1
Перейти к основанию 2
…………….
Введите новую переменную
t= log2 x
№3 Найти сумму наибольшего отрицательного и наименьшего положительного корней уравнения
4sin22x=2
Решение
4 sin22x=2
Примени формулу понижения степени sin22x=
Затем реши уравнение х=
Перебором
k=0, x=
k=-1, х=
k=1, x=
Найди наименьший положительный корень.
Найди наибольший отрицательный корень.
Затем найди сумму.
№4 Найдите сумму корней уравнения (3)·lg(1-x)=0
3=0 или lg (1-х) =0
Решение
ОДЗ х:
(3х-81) lg(1-x)=0
(3х-81)=0 или lg(1-x)=0
3 группа. Карточка- помощник
№1 Решите уравнение
-5=х2-3х
В ответе укажите среднее арифметическое его корней.
Решение
Введите новую переменную
t=x2 -3x
-5=t
Решите полученное уравнение
№2 Найдите произведение всех корней уравнения
(5· lg (17-6x-x2)=0
Решение
Укажите ОДЗ х: 17-6x-x20
Вспомни, когда произведение двух множителей равно нулю.
№3 Найдите сумму корней уравнения sin 2x·(tgx-1) =0, принадлежащих промежутку
[ 0; 2π ]
Решение
Укажите ОДЗ х: x
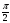 +
+ ,
Решите уравнение
sin 2x · (tgx-1) =0
………………….
x= 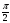 k, k
k, k  z или x=
z или x= + π k, k
 z
z
1) x= 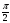 k, k
k, k  z , x
z , x  [0; 2 π] , х
[0; 2 π] , х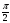 + π k, k
+ π k, k  z
z
х= π k, k  z 0
z 0
2) х= +π k, k
 z ,х
z ,х  [0;2 π] ,
[0;2 π] ,
х
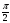 + π k, k
+ π k, k  z
z
х =+
,

0+
2
3) Найдите сумму корней уравнения
№4 Решите уравнение
=2х-2
Решение
Примени =
=
 а, а
а, а0
-а, а

Группа 1
№1 Решите уравнение
=х-1
(если уравнение имеет более одного корня, то в ответе укажите их произведение)
№2 Найдите сумму корней уравнения
49 · 72х-50 · 7х+1=0
№3 Укажите число корней уравнения
(х-6)· cosx=(x-6)
Дополнительное задание
№4 Решите уравнение
log0,3(7x+5) – log0,33=log0,34
Домашнее задание
№1 Решите уравнение
а) 2х+3-8х+1=0
б) log3x + log3(3х-2)=log35
в)+2=0
№2 Решите уравнение
·
=4
В ответе укажите число корней
Группа 2
№1 Решите уравнение
2-х=0
В ответе укажите разность между наибольшим и наименьшим корнем.
№2 Найдите произведение корней уравнения
log32 х –3 log22х=10/logх2
№3 Найти сумму наибольшего отрицательного и наименьшего положительного корней уравнения
4sin22x=2
Дополнительное задание
№4 Найдите сумму корней уравнения (3х-81) lg(1-x)=0
Домашнее задание
№1 Найдите корень (или сумму корней , если их несколько) уравнения
а)()(3х-8) (2-х)-5=125х
б) log2,5x = log0,44+log0,40,5
№2 Решите уравнение
-
=6

№3 Найдите количество корней уравнения
log2 (sinx-1) = log2 (
Группа 3
№1Решите уравнение
-5=х2-3х
В ответе укажите среднее арифметическое его корней.
№2 Найдите произведение всех корней уравнения
(5x-77-625) lg (17-6x-x2)=0
№3 Найдите сумму корней уравнения sin 2x (tgx-1) =0, принадлежащих промежутку
[ 0; 2π ] Ответ запишите в градусах
Дополнительное задание
№4 Решите уравнение
2=2х-2
Домашнее задание
1.Решите уравнение
lg(2х-1)+ lg
=1
б) 9-7·3
=18
в) 5х ·2=40
Найдите число корней уравнений
-
·
=0



ПАМЯТКА ПРИ РЕШЕНИИ УРАВНЕНИЙ
Основным шагом в решении уравнения является преобразование уравнения к одному из простейших уравнений.
Полностью алгоритмизировать процесс преобразования нельзя, однако полезно знать наиболее употребительные приемы, общие для всех типов уравнений:
1. Замена уравнения h(f(x)) = h(g(x)) уравнением f(x)=g(x) этот метод можно применять
- при решении показательных уравнений переходим от уравнений
af(x) = ag(x) (a0, a = 1) к уравнению f(x) = g(x)
при решении логарифмических уравнений переходим от уравнения logaf(x) = logag(x) к уравнению f(x)=g(x);
- при решении иррациональных уравнений переходим от уравнения …… к уравнению

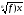 =
=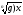
Этот метод применим только в том случае, когда функция y= h(x) – монотонная функция, которая каждое свое значение принимает по одному разу (либо функция возрастающая, либо убывающая на всей области определения)
2. Метод разложения на множители
уравнение f(x) g(x) h(x)=0 можно, заменить совокупностью уравнений f(x)=0, g(x)=0, h(x)=0
3. Метод введения новой переменной
- если уравнение f(x) =0 удалось преобразовать к виду p(g(x))=0 , то нужно ввести новую переменную t=g(x), решить уравнение p(x)=0, затем решить совокупность уравнений g(x)=t1 , g(x)=t2;…..; g(x)=tn где t1 , t2,……tn- корни уравнения p(t)=0
4. Функционально-графический метод
-для решения уравнения f(x)=g(x); нужно построить графики функций y=f(x), y=g(x) и найти точки их пересечения корнями уравнения служат абсциссы этих точек.
- если на промежутке X наибольшее значение одной из функций y=f(x), y=g(x) равно А и наименьшее значение другой функции тоже равно А, то уравнение f(x)=g(x) равносильно на промежутке X системе уравнений
f(x)=А
g(x)=А

 Получите свидетельство
Получите свидетельство Вход
Вход












 Статья "Подготовка учащихся к итоговой аттестации за курс средней школы" (198.96 KB)
Статья "Подготовка учащихся к итоговой аттестации за курс средней школы" (198.96 KB)
 0
0 451
451 1
1 Нравится
0
Нравится
0




