| Название урока и класс | «Сокращение дробей» 6 класс | ||
| Цели | Вывести правило сокращения дробей, используя признаки делимости чисел и основного свойства дроби, и уметь применять его на практике | ||
| Планируемые результаты | Ученики научатся: 1. Сформулировать правило сокращения дробей 2. оперировать понятием несократимой дроби 3. Научаться применять эти правила на практике 4. Работать индивидуально, в парах, аргументировать и отстаивать свое мнение | ||
| Этап урока | время | Деятельность учителя | Ссылка |
| Организационный момент | 2 мин. | Приветствует детей, проверяет их готовность к уроку. Настраивает на активную работу. Откройте тетради, запишите число и "Классная работа". |
|
| Актуализация знаний | 8 мин. | 1.Что называется делителем числа a? - Пройдите тест «Понятие делимости» 2. Что называется НОД чисел a и b? - Пройдите самостоятельно тест «Наибольший общий делитель» 3. Какие числа называются взаимно простыми? 5. Признаки делимости на 2, 5, 10, 3, 9. 6. Сформулируйте основное свойство дроби - Решите самостоятельно тест «Основное свойство дроби»
| https://uchi.ru/teachers/groups/6524464/subjects/1/course_programs/6/cards/74106 https://uchi.ru/teachers/groups/6524464/subjects/1/course_programs/6/cards/74122 https://uchi.ru/teachers/groups/6524464/subjects/1/course_programs/6/cards/74069 |
| Самоопределение к деятельности | 5 мин. | А теперь откроем учебник, стр. 40, задача № 250. Прочтите, пожалуйста, вслух задачу.
О чем задача? Сколько было рабочих? Что говорится в задаче об этих рабочих? Что нужно найти? Что для этого нужно знать?
Я даю вам 2-3 минутки, чтобы вы в парах обсудили решение данной задачи.
Выслушать мнения учащихся, записать решение на доске: 1) 6 : 16 = 2) 15 : 24 = – Как выяснить, кто из них затратил времени больше?
– Умеем ли мы сравнивать дроби с разными знаменателями? – А с одинаковыми знаменателями? – Можем ли мы из этих дробей получить равные им дроби, но с другими знаменателями? – Какое свойство мы для этого используем?
|
|
| Введение понятия |
| – Итак, мы с вами применили основное свойство дроби, заменили дроби на равные им путём деления числителя и знаменателя на одно и то же число. Получилась дробь, значение которой равно данной дроби, но с меньшим числителем и знаменателем Такое преобразование называют …. СОКРАЩЕНИЕМ ДРОБЕЙ
– Тема нашего урока «Сокращение дробей». Запишите её в тетрадь. |
|
| Работа по теме урока |
| Возникает вопрос «Когда можно сокращать?». Чтобы ответить на этот вопрос решим все вместе тест. Сократить дроби, комментируя | https://uchi.ru/teachers/groups/6524464/subjects/1/course_programs/6/cards/74076 |
| Закрепление материала |
| Задание решать будем самостоятельно, к доске пойдут два человека и будут выполнять задание на доске, потом мы вместе все проверим.
| https://uchi.ru/teachers/groups/6524464/subjects/1/course_programs/6/cards/74072 |
| Подведение итогов урока Домашнее задание |
| - Подходит к завершению наш урок, пора подвести итоги. - Запишите домашнее задание: – Что значит сократить дробь? – Что меняется при сокращении дроби? – Какая дробь называется несократимой? – Поставьте себе оценку за урок.
Урок окончен! Вы все молодцы! Спасибо за работу!
|
|

 Получите свидетельство
Получите свидетельство Вход
Вход


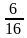 (ч) затратил первый рабочий
(ч) затратил первый рабочий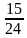 (ч) затратил второй рабочий
(ч) затратил второй рабочий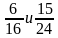
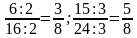
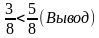









 Сокращение дробей, 6 класс (20.15 KB)
Сокращение дробей, 6 класс (20.15 KB)
 0
0 190
190 1
1 Нравится
0
Нравится
0






