
Системы счисления
9 класс

Двоичное кодирование в компьютере
Вся информация, которую обрабатывает компьютер должна быть представлена двоичным кодом с помощью двух цифр: 0 и 1 . Эти два символа принято называть двоичными цифрами или битами , или двоичным кодом .
С точки зрения технической реализации использование двоичной системы счисления для кодирования информации оказалось намного более простым, чем применение других способов.
Недостаток двоичного кодирования – длинные коды. Но в технике легче иметь дело с большим количеством простых элементов, чем с небольшим числом сложных.
0 – отсутствие электрического сигнала;
1 – наличие электрического сигнала .

С помощью двух цифр 0 и 1 можно закодировать любое сообщение. Это явилось причиной того, что в компьютере обязательно должно быть организованно два важных процесса: кодирование и декодирование.
Кодирование – преобразование входной информации в форму, воспринимаемую компьютером, т.е. двоичный код.
Декодирование – преобразование данных из двоичного кода в форму, понятную человеку.
Способы кодирования и декодирования информации в компьютере, в первую очередь, зависит от вида информации, а именно, что должно кодироваться: числа, текст, графические изображения или звук.
Запись в тетрадь (курсив)

Запись в тетрадь
Виды систем счисления
СИСТЕМЫ СЧИСЛЕНИЯ
ПОЗИЦИОННЫЕ
НЕПОЗИЦИОННЫЕ
В непозиционных системах счисления величина , которую обозначает цифра, не зависит от положения в числе.
В позиционных системах счисления величина , обозначаемая цифрой в записи числа, зависит от её положения в числе ( позиции ).
XXI
211

Непозиционные системы счисления
Ярким примером фактически непозиционной системы счисления является римская , в которой в качестве цифр используются латинские буквы:
I обозначает 1, V - 5, X - 10, L - 50, C - 100, D - 500, M -1000.
Натуральные числа записываются при помощи повторения этих цифр. Например, II = 1 + 1 = 2, здесь символ I обозначает 1 независимо от места в числе.
Для правильной записи больших чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц.
Пример: число 1789. Одна тысяча M, семь сотен DCC, восемьдесят LXXX, девять IX. Запишем их вместе: MDCCLXXXIX.
MDCCLXXXIX=1000+(500+100+100)+(50+10+10+10)+(10-1)=1789
Для изображения чисел в непозиционной системе счисления нельзя ограничится конечным набором цифр. Кроме того, выполнение арифметических действий в них крайне неудобно.

Первые позиционные системы счисления
Самой первой такой системой, когда счетным "прибором" служили пальцы рук, была пятеричная .
Следующей возникла двенадцатеричная система счисления. Возникла она в древнем Шумере. Возможно, что она возникала у них из подсчёта фаланг на руке большим пальцем.
На ее широкое использование в прошлом указывает сохранившиеся в ряде стран способы отсчета времени, денег и соотношения между некоторыми единицами измерения. Год состоит из 12 месяцев, а половина суток состоит из 12 часов.
Элементом двенадцатеричной системы в современности может служить счёт дюжинами.
Английский фунт состоит из 12 шиллингов.

Первые позиционные системы счисления
Следующая позиционная система счисления была придумана еще в Древнем Вавилоне, причем вавилонская нумерация была шестидесятеричная , т.е. в ней использовалось шестьдесят цифр!
В более позднее время использовалась арабами, а также древними и средневековыми астрономами. Шестидесятеричная система счисления, как считают исследователи, являет собой синтез уже вышеупомянутых пятеричной и двенадцатеричной систем.
В настоящее время наиболее распространены десятичная , двоичная , восьмеричная и шестнадцатеричная системы счисления.

Десятичная система счисления
Запись в тетрадь (курсив)
Десятичная система счисления — позиционная система счисления по основанию 10.
Для записи чисел используются символы 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , называемые арабскими цифрами.
Предполагается, что основание 10 связано с количеством пальцев на руках у человека.
Наиболее распространённая система счисления в мире.

Двоичная система счисления
Запись в тетрадь (курсив)
Двоичная система счисления — позиционная система счисления с основанием 2.
Используются цифры 0 и 1.
Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и удовлетворяет требованиям:
- Чем меньше значений существует в системе, тем проще изготовить отдельные элементы.
- Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать.
- Простота создания таблиц сложения и умножения — основных действий над числами

Алфавит двоичной, восьмеричной, десятичной и шестнадцатеричной систем счисления
Запись в тетрадь
Система счисления
Основание
Двоичная
Алфавит цифр
2
Восьмеричная
8
0, 1
Десятичная
10
Шестнадцатеричная
0, 1, 2, 3, 4, 5, 6, 7
16
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Количество используемых цифр называется основанием системы счисления .
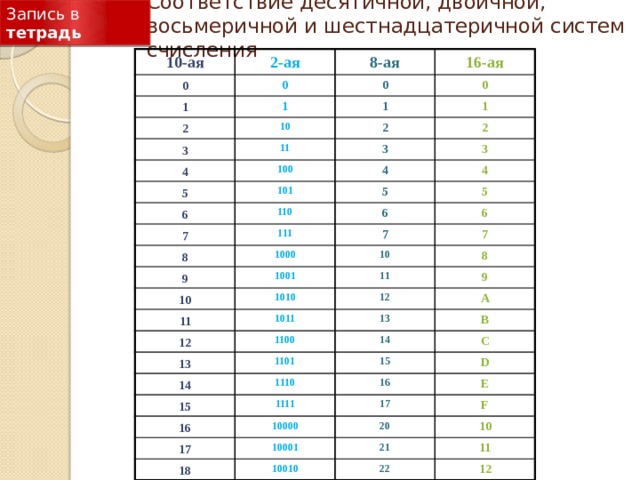
Соответствие десятичной, двоичной, восьмеричной и шестнадцатеричной систем счисления
Запись в тетрадь
10-ая
2-ая
0
8-ая
1
0
16-ая
2
0
1
1
0
3
10
11
4
2
1
2
3
100
5
6
3
4
101
7
110
5
4
5
6
111
8
6
7
1000
9
7
10
1001
10
8
11
1010
11
9
12
1011
12
A
13
1100
13
14
B
14
1101
15
1110
15
C
D
16
1111
16
17
E
17
10000
18
10001
20
F
10
21
10010
11
22
12

Запись в тетрадь
Перевод целых десятичных чисел
в 2, 8, 16-ую системы счисления

Представим число 67 записанное в десятичной системе счисления в позиционных системах счисления:
двоичной, восьмеричной, шестнадцатеричной.
67 10 = А 2
67 10 = А 8
67 10 = А 16

Запись в тетрадь
Представим число 67 10
в двоичной системе счисления:
2
67
66
2
33
Ответ: 67 10 = 1000011 2
32
2
1
16
2
16
8
1
2
4
0
8
2
4
2
0
2
1
0
0
14

Запись в тетрадь
Представим число 67 10
в восьмеричной системе счисления:
8
67
64
8
8
8
3
1
0
Ответ: 67 10 = 103 8
15

Запись в тетрадь
Представим число 67 10
в шестнадцатеричной системе счисления:
16
67
64
4
3
Ответ: 67 10 = 43 16
16

Запись в тетрадь
Правила перехода
Из десятичной системы счисления
в позиционные системы счисления:
- Разделить десятичное число на основание системы счисления. Получится частное и остаток.
- Выполнять деление до тех пор, пока последнее частное не станет меньшим основания новой системы счисления.
- Записать последнее частное и все остатки в обратном порядке. Полученное число и будет записью в новой системы счисления .

Запись в тетрадь
Перевод из 2, 8, 16-ой систем
счисления в десятичную

Запись в тетрадь
Представим число 123 10
в шестнадцатеричной системе счисления:
16
123
112
7
11
В
Ответ: 123 10 = 7В 16
19

Запись в тетрадь
Представим число 1000011 2
в десятичной системе счисления:
1 6 0 5 0 4 0 3 0 2 1 1 1 0 = 1∙2 0 +1∙2 1 +0∙2 2 +0∙2 3 +0∙2 4 +0∙2 5 +1∙2 6 =
1+2+0+0+0+0+64= 67 10
а 0 =1
Свойство степени
Ответ: 1000011 2 =67 10

Представим число 103 8
Запись в тетрадь
в десятичной системе счисления:
1 2 0 1 3 0 = 3∙8 0 +0∙8 1 +1∙8 2 =3+0+64=67 10
Ответ: 103 8 =67 10

Представим число 7В 16
Запись в тетрадь
в десятичной системе счисления:
7 1 В 0 = 11∙16 0 +7∙16 1 =11+112=123 10
Ответ: 7В 16 = 123 10

Запись в тетрадь
Перевод 2 8 СС
Очень просто! Направо и налево от точки откладываем триады - группы по три цифры, после чего записываем их в соответствующем 8-ном виде. Неполные триады дополняются нулями.
Пример:
1011010,01101 2 = 001 011 010,011 010 2 = 132,32 8
Обратно - с точностью до наоборот:
257,31 8 = 010 101 111, 011 001 2 = 10101111,011001 2
Соответствие значений систем счисления смотри на слайде №11!!!

Запись в тетрадь
Системы счисления, используемые в ЭВМ (с основанием 2 n )
Перевести число 1100101001101010111 2
в восьмеричную систему счисления
001 100 101 001 101 010 111
1 4 5 1 5 2 7
Получаем 1451527 8

Запись в тетрадь
Перевод 2 16 СС
Очень просто! Направо и налево от точки откладываем тетрады - группы по четыре цифры, после чего записываем их в соответствующем 16-ном виде. Неполные тетрады дополняются нулями.
Пример:
1011010110,011001 2 = 0010 11 01 0110,011 010 2 = 132,32 8
Обратно - с точностью до наоборот:
257,31 8 = 010 101 111, 011 001 2 = 10101111,011001 2
Соответствие значений систем счисления смотри на слайде №11!!!

Запись в тетрадь
Перевести число 1100101001101010111 2
в шестнадцатеричную систему счисления
0110 0101 0011 0101 0111
6 5 3 5 7
Получаем 65357 16

Тест
№
Согласны ли вы с утверждением
1
Да
Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.
2
Нет
Все системы счисления делятся на три большие группы: позиционные, непозиционные и полупозиционные.
3
В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе.
4
5
Основанием двоичной системы счисления является число 4
Число А21СFD4 записано в шестнадцатеричной системе счисления.
6
Число 156 7 записано с ошибкой.
7
Число 10, записанное в десятичной системе счисления, в двоичной системе счисления записывается как 1011
8
Число 10, записанное в десятичной системе счисления, меньше числа 10, записанного в восьмеричной системе счисления.
9
Число 3005,23 4 записано с ошибкой.
10
Число 6398 записано в восьмеричной системе счисления.
Не забудьте сдать учителю!!!

Спасибо за внимание!

 Получите свидетельство
Получите свидетельство Вход
Вход












 Системы счисления. Перевод чисел из одной системы счисления в другую. (366.07 KB)
Системы счисления. Перевод чисел из одной системы счисления в другую. (366.07 KB)
 0
0 407
407 10
10 Нравится
0
Нравится
0




