
Урок алгебры в 7-ом классе
«Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций»
Подготовила: Богатикова. О.Б,
учитель математики МОУ Новоталицкая СОШ


«Мне приходится делить свое время между политикой и уравнениями. Однако уравнения, по – моему, гораздо важнее, потому что политика существует только для данного момента, а уравнения
……… .
Альберт Энштейн.
будут существовать вечно.
«Недостаточно лишь понять задачу, необходимо желание решить ее. Где есть желание, найдется путь.»
Джордж Пойа.
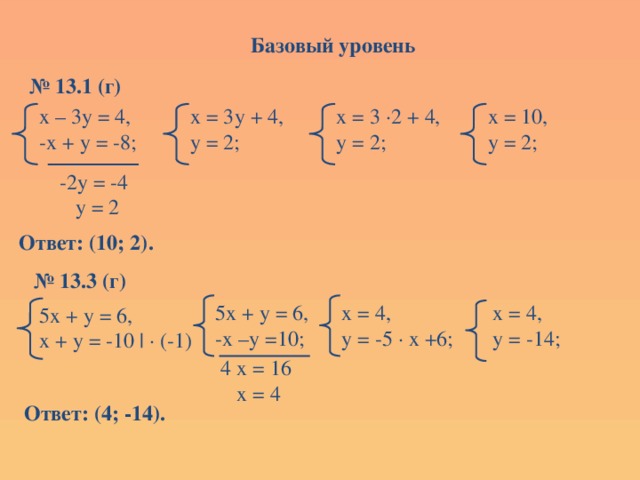
Базовый уровень
№ 13.1 (г)
х = 3у + 4,
х – 3у = 4,
х = 10,
х = 3 ∙2 + 4,
-х + у = -8;
у = 2;
у = 2;
у = 2;
-2у = -4
у = 2
Ответ: (10; 2).
№ 13.3 (г)
х = 4,
5х + у = 6,
х = 4,
у = -5 ∙ х +6;
-х –у =10;
у = -14;
5х + у = 6,
х + у = -10 | ∙ (-1)
4 х = 16
х = 4
Ответ: (4; -14).

Что мы знаем?
Что мы умеем?
- Система двух линейных уравнений с двумя переменными;
- Решение системы;
- Что значит решить систему?
- Методы решения систем.
- Проверять, является ли пара (х;у) решением системы;
- Решать системы различными способами;
- Находить в системе неизвестные коэффициенты, зная ее решение.
Где эти знания и умения возможно применить?

8
7
6
5
4
3
2
1

« Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций»

Математическая модель реальной ситуации
− это алгебраическое уравнение, неравенство
или система уравнений (неравенств),
в которые входят переменные, поставленные по правилам математического языка в соответствие объектам реальной ситуации.
Основные этапы математического моделирования:
- Составление математической модели.
- Работа с математической моделью.
- Обработка полученного решения и запись ответа.

В секции легкой атлетики занимаются 29 школьников, причем мальчиков на 3 больше, чем девочек. Сколько мальчиков и сколько девочек в секции?
Решение: Пусть в секции х девочек, и у мальчиков.
Тогда, по условию задачи составляем и решаем систему уравнений.
у – х = 3,
у + х = 29;
х = 13,
х = 29 – 16,
у = 16;
у = 16;
2 у = 32
у = 16
Ответ: 16 мальчиков, 13 девочек.

Физкультминутка


Задача:
В кассе 136 монет пятирублевого и двухрублевого достоинства на сумму 428 рублей. Сколько монет каждого достоинства в кассе?
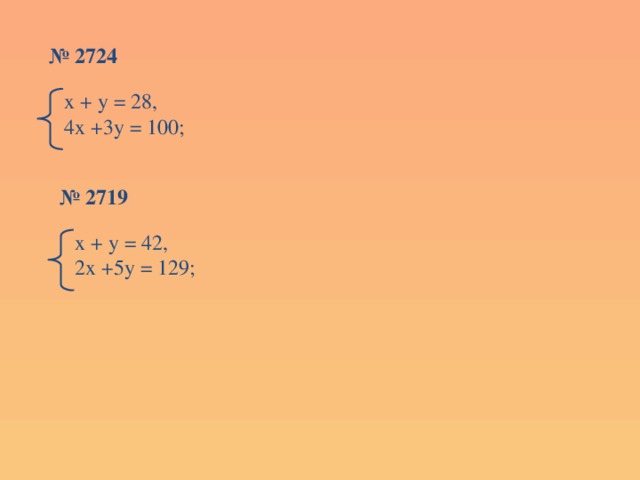
№ 2724
х + у = 28,
4х +3у = 100;
№ 2719
х + у = 42,
2х +5у = 129;

Домашнее задание:
- Решить систему № 2724, 2719 (из сборника).
- Решить задачу № 12.13 ( по желанию)
- Проклассифицировать задачи №14.1-14.15 по типам: «а»-задачи на движение, «б»-задачи о числах, «в» - задачи на совместную работу
8
7
6
5
4
3
2
1


Система уравнений
Если даны два уравнения, например,
a 1 x + b 1 y + c 1 = 0 и a 2 x + b 2 y + c 2 = 0
с неизвестными x и y, и поставлена задача найти
такие пары значений ( x; y), которые одновременно
удовлетворяют и тому, и другому уравнениям,
то говорят, что заданные уравнения образуют систему уравнений.
Принята следующая форма записи:

Решение системы уравнений
Пусть дана система уравнений, например:
Пару значений ( x; y), которая одновременно
удовлетворяет и тому, и другому уравнениям системы,
называют решением системы уравнений.

Решить систему -
это значит найти все ее решения или установить, что их нет.



 Получите свидетельство
Получите свидетельство Вход
Вход






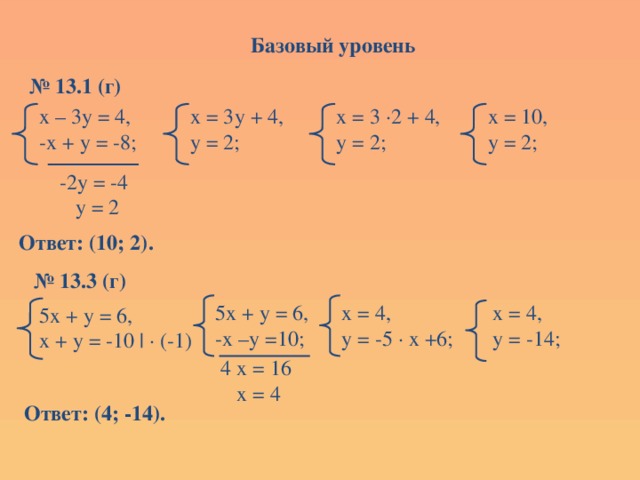








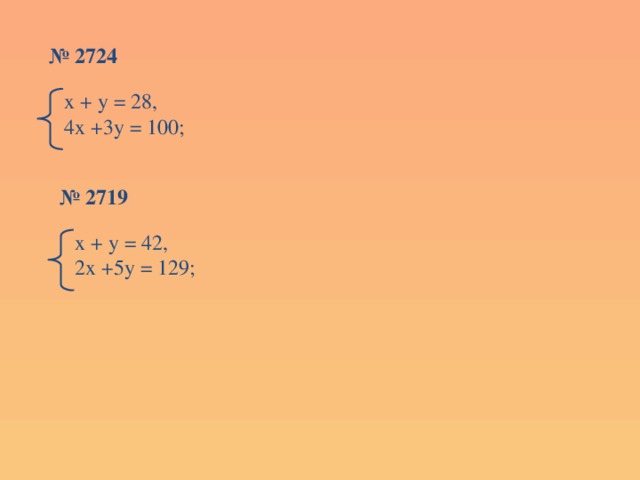
















 Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций (0.84 MB)
Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций (0.84 MB)
 0
0 957
957 99
99 Нравится
0
Нравится
0


