Синус, косинус, тангенс

Синус, косинус и тангенс угла.

Цель урока

• Что называется синусом, косинусом, тангенсом острого угла прямоугольного треугольника?

• Какое равенство называют основным тригонометрическим тождеством?
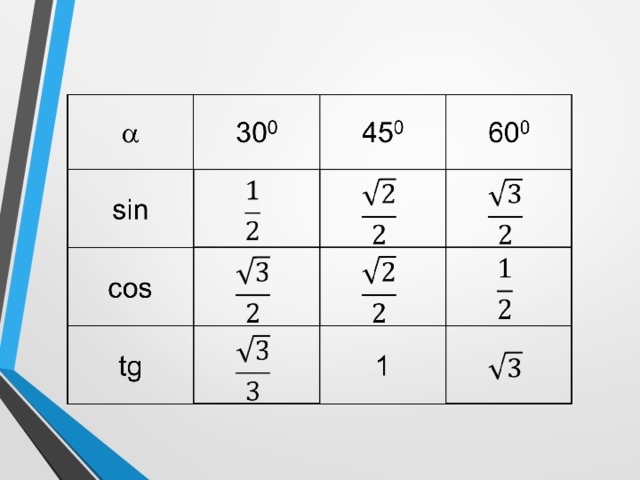
• Чему равны значения синуса, косинуса и тангенса для углов 30 0 , 45 0 и 60 0 ?

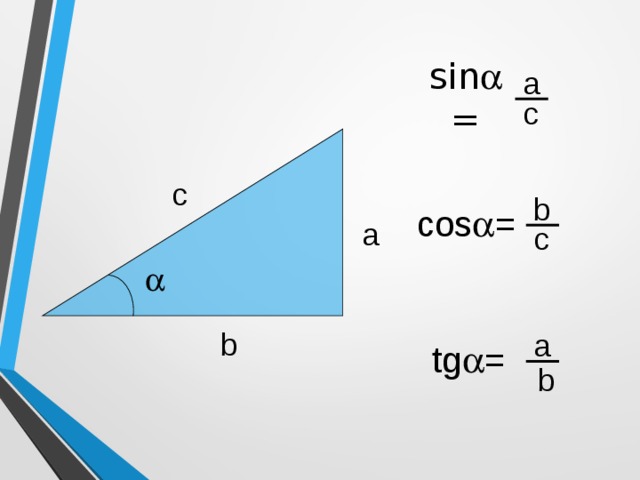
sin  =

a

c

c

cos  =

b

a

c



tg  =

b

a

b

Основное тригонометрическое тождество:

sin 2  +cos 2  =1

Изучение нового материала

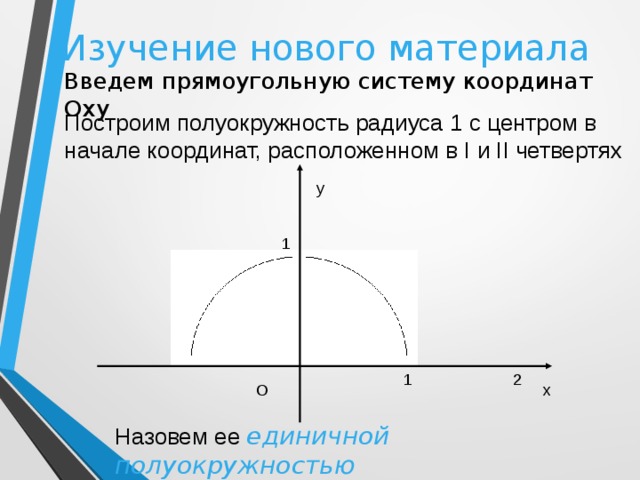
Введем прямоугольную систему координат Оху

Построим полуокружность радиуса 1 с центром в начале координат, расположенном в I и II четвертях

у

1

1

2

х

О

Назовем ее единичной полуокружностью

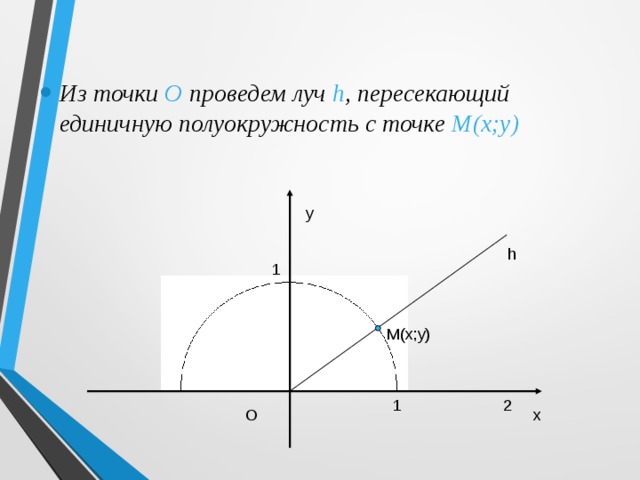
• Из точки О проведем луч h , пересекающий единичную полуокружность с точке М(х;у)

у

h

1

М(х;у)

1

2

х

О

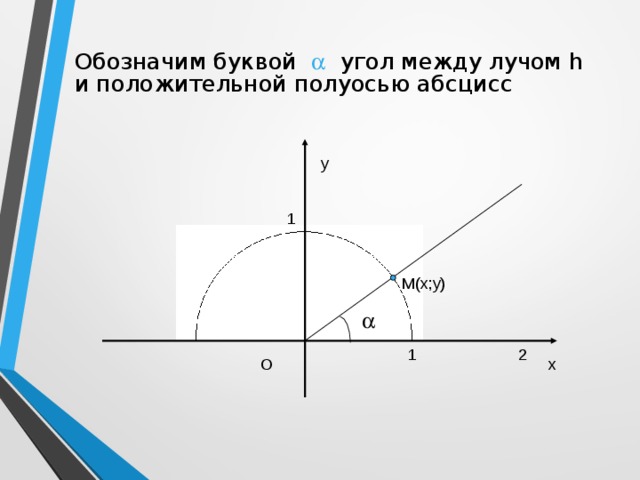
Обозначим буквой  угол между лучом h и положительной полуосью абсцисс

у

1

М(х;у)



1

2

х

О

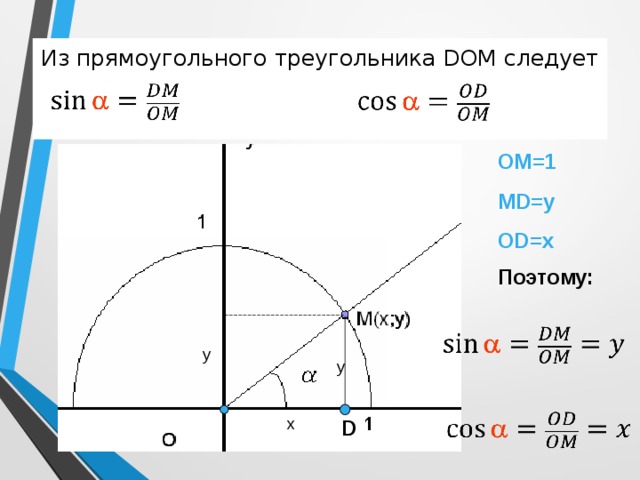
Из прямоугольного треугольника DOM следует

ОМ=1

MD=y

OD=x

Поэтому:

y

y

x

D

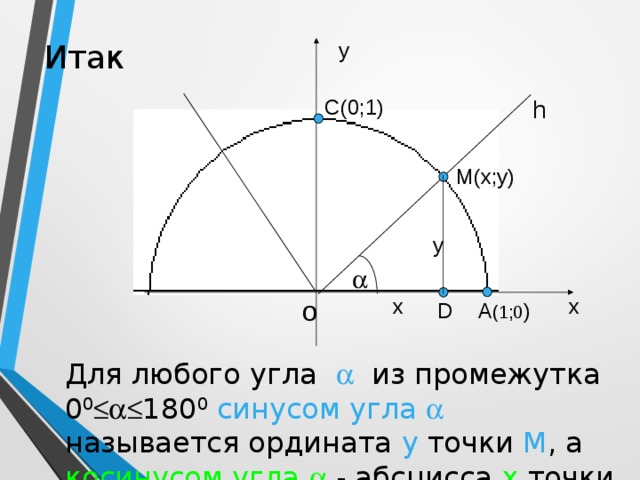
Итак

у

h

C(0;1)

M(x;y)

y



о

х

х

D

A (1;0 )

Для любого угла  из промежутка 0 0  180 0 синусом угла  называется ордината у точки М , а косинусом угла  - абсцисса х точки М

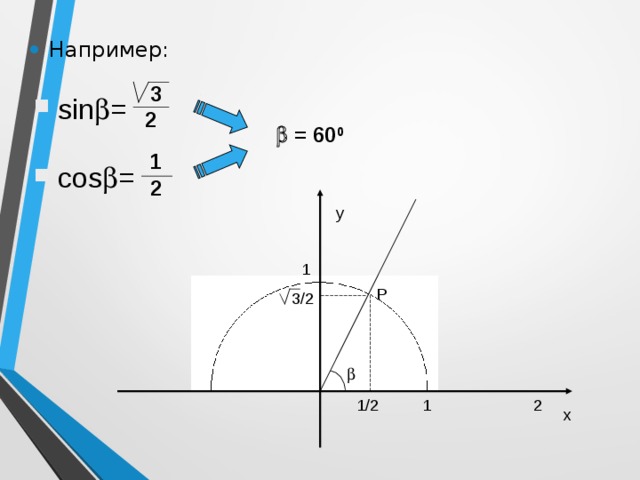
• Например:

3

• sin  =

2

 = 60 0

1

• cos  =

2

у

1

Р

3/2



1/2

2

1

х

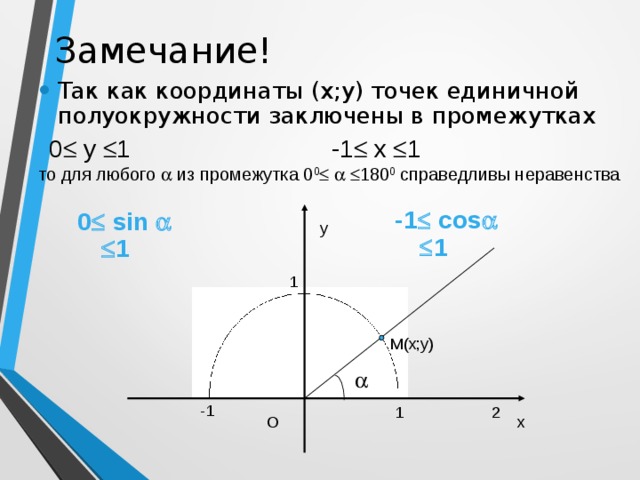
Замечание!

• Так как координаты (х;у) точек единичной полуокружности заключены в промежутках

-1  х  1

0  у  1

то для любого  из промежутка 0 0    180 0 справедливы неравенства

• то для любого  из промежутка 0 0    180 0 справедливы неравенства

-1  cos   1

0  sin   1

у

1

М(х;у)



-1

2

1

О

х

Найдем значения синуса, косинуса для углов 0 0 , 90 0 и 180 0

Для этого рассмотрим лучи ОА, ОС, ОВ, соответствующие этим углам

sin 0 0 =0

cos 0 0 =1

cos90 0 =0

sin90 0 =1

у

С(0;1)

sin 180 0 =0

cos 180 0 =-1

В(-1;0)

О

2

А(1;0)

х

Тангенс угла

Тангенсом угла  (  90 0 )

называется отношение sin  к cos 

При  = 90 0 tg  не определен

знаменатель обращается в нуль!

tg 90 0 = sin90 0

cos90 0

cos90 0 = 0

tg  = sin 

cos 

Найдите tg0 0 , tg180 0

tg0 0 =0

tg180 0 =0

Итог урока: