Шаг за шагом к ЕГЭ по математике.

Шаг за шагом

к ЕГЭ по математике

10 класс

Подготовила : Ефимцева Ирина Васильевна.

Шаг за шагом

к ЕГЭ по математике

10 класс

Куз­не­чик пры­га­ет вдоль ко­ор­ди­нат­ной пря­мой в любом на­прав­ле­нии на еди­нич­ный от­ре­зок за один пры­жок. Куз­не­чик на­чи­на­ет пры­гать из на­ча­ла ко­ор­ди­нат. Сколь­ко су­ще­ству­ет раз­лич­ных точек на ко­ор­ди­нат­ной пря­мой, в ко­то­рых куз­не­чик может ока­зать­ся, сде­лав ровно 11 прыж­ков?

1

Посмотреть решение

За­ме­тим, что куз­не­чик может ока­зать­ся толь­ко в точ­ках с нечётными ко­ор­ди­на­та­ми, по­сколь­ку число прыж­ков, ко­то­рое он де­ла­ет, — нечётно. Мак­си­маль­но куз­не­чик может ока­зать­ся в точ­ках, мо­дуль ко­то­рых не пре­вы­ша­ет один­на­дца­ти. Таким об­ра­зом, куз­не­чик может ока­зать­ся в точ­ках: −11, −9, −7, −5, −3, −1, 1, 3, 5, 7, 9 и 11; всего 12 точек.

Ответ: 12.

Каж­дую се­кун­ду бак­те­рия де­лит­ся на две новые бак­те­рии. Из­вест­но, что весь объём од­но­го ста­ка­на бак­те­рии за­пол­ня­ют за 1 час. За сколь­ко се­кунд ста­кан будет за­пол­нен бак­те­ри­я­ми на­по­ло­ви­ну?

2

Посмотреть решение

За­ме­тим, что каж­дую се­кун­ду в ста­ка­не ста­но­вит­ся в два раза боль­ше бак­те­рий. То есть если в какой-то мо­мент бак­те­ри­я­ми за­пол­не­на по­ло­ви­на ста­ка­на, то через се­кун­ду будет за­пол­нен весь ста­кан. Таким об­ра­зом, пол­ста­ка­на будет за­пол­не­но через 59 минут и 59 се­кунд то есть через 3599 се­кунд.

Ответ: 3599.

3

На палке от­ме­че­ны по­пе­реч­ные линии крас­но­го, жёлтого и зелёного цвета. Если рас­пи­лить палку по крас­ным ли­ни­ям, по­лу­чит­ся 5 кус­ков, если по жёлтым — 7 кус­ков, а если по зелёным — 11 кус­ков. Сколь­ко кус­ков по­лу­чит­ся, если рас­пи­лить палку по ли­ни­ям всех трёх цве­тов?

Посмотреть решение

Каж­дый рас­пил уве­ли­чи­ва­ет ко­ли­че­ство кус­ков на один. То есть всего 4 крас­ные линии, 6 жёлтых и 10 зелёных. То есть вме­сте 20 линий. А кус­ков по­лу­чит­ся 21.

Ответ: 21.

4

Вы­черк­ни­те в числе 53164018 три цифры так, чтобы по­лу­чив­ше­е­ся число де­ли­лось на 15. В от­ве­те ука­жи­те ровно одно по­лу­чив­ше­е­ся число.

Посмотреть решение

Ответ: 53640 или 53160.

5

В клас­се учит­ся 25 уча­щих­ся. Не­сколь­ко из них хо­ди­ли в кино, 18 че­ло­век хо­ди­ли в театр, причём и в кино, и в театр хо­ди­ли 12 че­ло­век. Из­вест­но, что трое не хо­ди­ли ни в кино, ни в театр. Сколь­ко че­ло­век из клас­са хо­ди­ли в кино?

Посмотреть решение

12 че­ло­век хо­ди­ли и в кино, и в театр. А всего в театр хо­ди­ло 18 че­ло­век. Зна­чит, 6 че­ло­век хо­ди­ли толь­ко в театр.

Схо­ди­ли в театр или в кино и в театр, или ни­ку­да не хо­ди­ли - 12 + 6 + 3 = 21 че­ло­век. Зна­чит,  25 – 21 = 4 че­ло­ве­ка хо­ди­ли толь­ко в кино. И зна­чит всего в кино схо­ди­ло  12 + 4 = 16 че­ло­век.

Ответ: 16.

Весь класс

4

6

12

театр

кино

Никуда - 3

а). Решите уравнение

б). Найдите все корни этого уравнения, принадлежащие отрезку

Применим формулу приведения:

Название « синус» изменится на « косинус», т.к.

О четверти и о знаке не думаем, т.к. синус в квадрате.



Нам будет удобно записать решение в виде двух множеств , т.к. аналитическая запись ответа

в виде:

неудобна для

решения двойного неравенства.



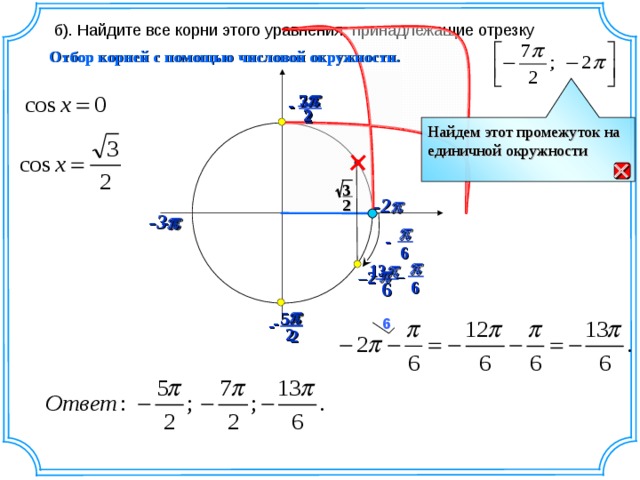
б). Найдите все корни этого уравнения, принадлежащие отрезку

Отбор корней с помощью числовой окружности.





7

3

-

-

2

2

Найдем этот промежуток на единичной окружности



3

2

-2 

-3 

- 



-

6





13

–



– 2

–

6

6





5

-

6

-

2

2

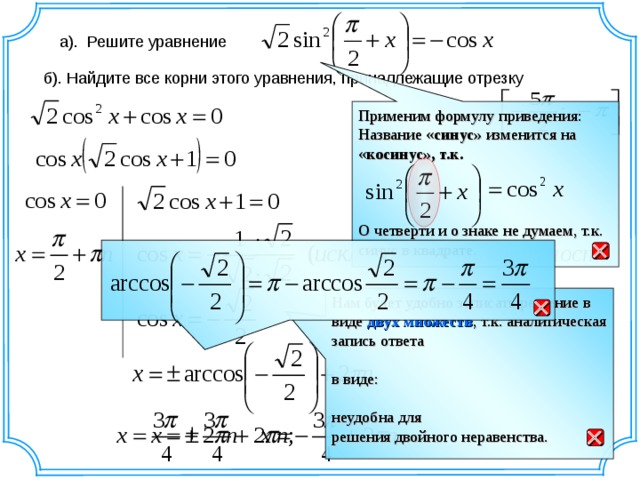
а). Решите уравнение

б). Найдите все корни этого уравнения, принадлежащие отрезку

Применим формулу приведения:

Название « синус» изменится на « косинус», т.к.

О четверти и о знаке не думаем, т.к. синус в квадрате.





Нам будет удобно записать решение в виде двух множеств , т.к. аналитическая запись ответа

в виде:

неудобна для

решения двойного неравенства.



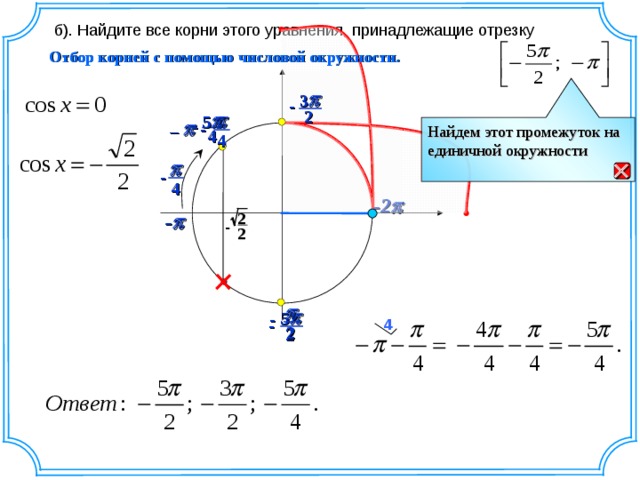
б). Найдите все корни этого уравнения, принадлежащие отрезку

Отбор корней с помощью числовой окружности.



3

-

2





5

-

-



–

Найдем этот промежуток на единичной окружности

4

4





-

4

-2 

2

- 

-

2





-

5

-

4

2

2

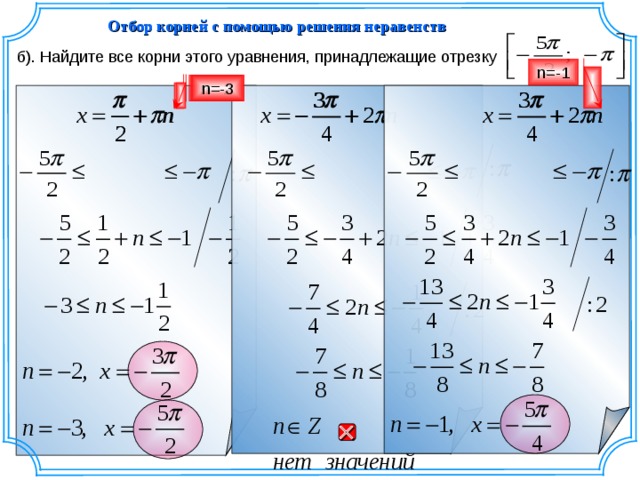
Отбор корней с помощью решения неравенств

б). Найдите все корни этого уравнения, принадлежащие отрезку

n= -1

n= -3

n= -2



Александр

Сергеевич

Пушкин

1799-1837

Каждый день идет там диво: Море вздуется бурливо, Закипит, подымет вой, Хлынет на берег пустой, Расплеснется в скором беге — И останутся на бреге Тридцать три богатыря, В чешуе златой горя, Все красавцы молодые, Великаны удалые, Все равны, как на подбор; Старый дядька Черномор С ними из моря выходит И попарно их выводит, Чтобы остров тот хранить И дозором обходить.[11]  

А ведь музыка и математика тесно связаны. Просто невероятно. Послушайте, как звучит число «ПИ» с точностью до 122 знаков после запятой от музыканта Д.Макдональда.

Диктант по заданиям ЕГЭ

(профильный уровень)

Государственная Третьяковская галерея , ГТГ (известна также как Третьяковка) — художественный музей в Москве , основанный в 1856 году купцом Павлом Третьяковым и имеющий одну из самых крупных в мире коллекций русского изобразительного искусства.

Рембрандт.

Молодая женщина, примеряющая серьги,

1657 г.

Рембрандт изображает молодую женщину, сидящую перед зеркалом и примеряющую серьги. Автора занимает проблема освещения, с помощью которого он выделяет интересующие его детали. Естественное кокетство жеста делает её образ предельно женственным.

Картина была создана в то время, когда имущество и коллекции объявленного банкротом художника были распроданы. Созданная на одном дыхании, картина каждым своим мазком говорит о переполняющих художника чувствах любви и восхищения. Их выдают и буйный

золотистый колорит, и горячее дыхание красных и розовых тонов.

Проверка оперативных разработок:

• оценка стоимости картины;

• оценка нанесенного ущерба музею;
• показания свидетелей.

По данным критиков и оценщиков живописи стоимость картины (копии) составляет 170000 рублей. Преступники, похитившие ее из музея, планируют продать ее на 65 % дороже. За сколько тысяч рублей похитители хотят продать картину?

170000 рублей. - 100%

100% + 65% = 165%

Х рублей. - 165%

Ответ: 280500

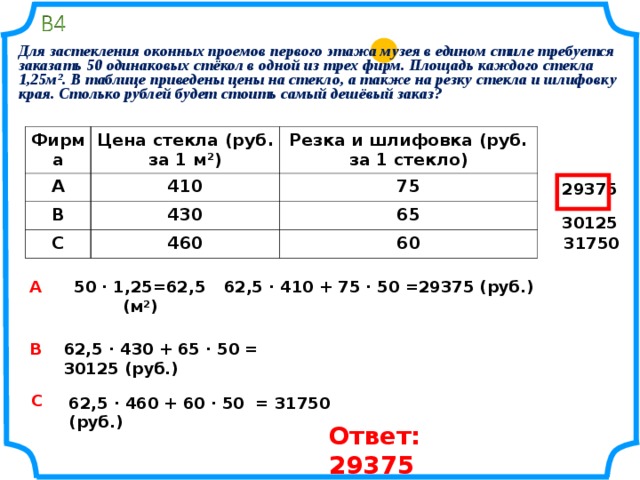
Для застекления оконных проемов первого этажа музея в едином стиле требуется заказать 50 одинаковых стёкол в одной из трех фирм. Площадь каждого стекла 1,25м². В таблице приведены цены на стекло, а также на резку стекла и шлифовку края. Столько рублей будет стоить самый дешёвый заказ?

Фирма

Цена стекла (руб. за 1 м²)

А

410

В

Резка и шлифовка (руб. за 1 стекло)

430

75

С

65

460

60

29375

30125

31750

А

50 · 1,25=62,5 (м²)

62,5 · 410 + 75 · 50 =29375 (руб.)

62,5 · 430 + 65 · 50 = 30125 (руб.)

В

С

62,5 · 460 + 60 · 50 = 31750 (руб.)

Ответ: 29375

В10 В среднем на 150 велосипедов приходится три неисправных. Найдите вероятность того, что преступникам попадутся исправные.

Всего 150 возможных исходов.

Благоприятен исход, когда выбранный велосипед окажется исправным.

Таких благоприятных исходов 150 – 3 = 147.

Находи вероятность,

как отношение благоприятных исходов 147 к числу всех возможных

исходов 150.

147/150 = 0,98

Ответ: 0,98

• Автомобиль преступников, движущий c я в начальный момент времени c о c коро c тью   м/ c , начал торможение на красный свет светофора c по c тоянным у c корением   м/ c . За t c екунд по c ле начала торможения он прошёл путь (м). Определите время, прошедшее от момента начала торможения, е c ли изве c тно, что за это время автомобиль проехал 30 метров.

Ответ: 4