Единый государственный экзамен
ИНФОРМАТИКА
Сборник кратких материалов и тренировочных заданий по теме «Основы логики»
Подготовила: Н. В. Брусникина
учитель информатики и ИКТ МБОУ СОШ №2 г. Кстово Нижегородской обл.
2014 г
В этот сборник включены основные понятия математической логики с определениями и примерами, а также все возможные обозначения логических операций. Даются алгоритмы построения таблиц истинности и решения логических задач. Приводятся тренировочные задания из нескольких источников: открытого сегмента федерального банка тестовых заданий, демонстрационных вариантов ЕГЭ прошлых лет, учебно-тренировочные материалы из книги «ЕГЭ. Информатика» (Крылов С.С., Лещинер В.Р., Супрун П.Г., Якушкин П.А.; Под ред. Лещинера В.Р. – М.: Интеллект-Центр, 2005,2006), «Самое полное издание типовых вариантов реальных заданий ЕГЭ 2010» ФИПИ, материалы с сайта К. Полякова (http://kpolyakov.narod.ru).
В сборник включены варианты решений части тестовых заданий – наиболее типичных или, наоборот, имеющих свои особенности, подчеркиваются проблемы, возникающие при решении данного класса задач. Задания приводятся из всех разделов темы «Логика», входящих в тестовые задания ЕГЭ, включая части А и Б.
В сборнике проводится сквозная нумерация заданий. Рядом с каждым номером указывается уровень задания и год, в который задание было включено в ЕГЭ.
В конце сборника приводятся ответы ко всем заданиям.
Сборник может быть использован учителями информатики при подготовке учащихся к ЕГЭ, а так же учащимися при самоподготовке в качестве дополнительного тренировочного материала.
Основные понятия алгебры логики
Логическая переменная – это простое высказывание.
Высказывание – повествовательное предложение, о котором можно сказать истинно оно или ложно.
Логические переменные обозначаются прописными и строчными латинскими буквами (a-z, A-Z) и могут принимать всего два значения – 1, если высказывание истинно, или 0, если высказывание ложно.
Примеры высказываний:
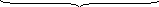
А = 1
В= 0
Логическая функция – это сложное высказывание, которое получается в результате проведения логических операций над простыми высказываниями.
Для образования сложных высказываний наиболее часто используются базовые логические операции, выражаемые с помощью логических связок «и», «или», «не».
Например,
![]()
![]() F(A,B) = {Лил дождь, и дул холодный ветер} = А и В.
F(A,B) = {Лил дождь, и дул холодный ветер} = А и В.
В
А
F(A,B,C)={Дети пели или играли и не расходились} = А или В и не С.
Значение логической функции зависит от значений входящих в нее логических переменных. Поэтому значение логической функции можно определить с помощью специальной таблицы (таблицы истинности), в которой перечислены все возможные значения входящих логических переменных и соответствующие им значения функции.
Основные логические операции
Отрицание (инверсия), от лат. Inversion – переворачиваю:
Соответствует частице НЕ, словосочетаниям НЕВЕРНО, ЧТО или НЕ ЯВЛЯЕТСЯ ИСТИНОЙ, ЧТО;
Обозначение: не А, А, 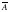 , not
, not
Таблица истинности:
| А | 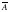
|
| 0 | 1 |
| 1 | 0 |
Инверсия логической переменной истинна, если сама переменная ложна, и, наоборот, инверсия ложна, если переменная истинна.
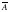 = {Неверно, что на улице идет снег}= {На улице не идет снег}
= {Неверно, что на улице идет снег}= {На улице не идет снег}
Логическое сложение (дизъюнкция), от лат. disjunctio – различаю:
Соответствует союзу ИЛИ;
Обозначение: V, +, или, or, ;
Таблица истинности:
| A | B | A V B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Дизъюнкция ложна тогда и только тогда, все, входящие в нее высказывания ложны.
Логическое умножение (конъюнкция), от лат. konjunctio – связываю:
Соответствует союзу И;
Обозначение: , •, , и, and, &;
Таблица истинности:
| A | B | A /\ B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Конъюнкция истинна тогда и только тогда, все, входящие в нее высказывания истинны.
С помощью базовых логических операций можно получить дополнительные логические операции:
Импликация (логическое следование), от лат. implicatio –тесно связываю:
| A | B | АВ |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Импликация истинна всегда, за исключением случая, когда А истинно, а В ложно (т.е. из истинной предпосылки не может вытекать ложный вывод).
А
В

Легко доказать, что F = A B = 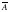 V B
V B
Эквиваленция (равнозначность), от лат. aequivalens – равноценное:
ЭКВИВАЛЕНТНО
Необходимо и достаточно для
Тогда и только тогда, когда;
Обозначение: =, , , , ;
Таблица истинности:
| A | B | А=В |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Эквиваленция истинна тогда и только тогда, когда все, входящие в нее высказывания, одновременно либо истинны, либо ложны.
Логическая операция Эквиваленция выражается через базовые логические операции следующим образом:

А В равносильно выражению (A V 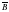 ) /\ (
) /\ (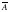 V B)
V B)
Построение таблиц истинности для логических функций
При построении таблицы истинности необходимо учитывать порядок выполнения логических операций. Операции в логическом выражении выполняются слева направо с учетом скобок в следующем порядке:
1. инверсия;
2. конъюнкция;
3. дизъюнкция;
4. импликация и эквивалентность.
Для изменения указанного порядка выполнения логических операций используются круглые скобки.
Алгоритм построения таблиц истинности логических функций
определить число логических переменных данной логической функции;
Определить количество строк таблицы по формуле: Q=2n , где n - количество логических переменных.
определить количество логических операций и их порядок;
определить количество столбцов таблицы по формуле:
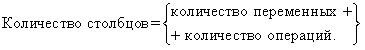
записать в таблицу все возможные наборы значений логических переменных;
записать в таблицу логические операции в порядке приоритета и заполнить столбцы результатами выполнения логических операций.
Пример. Построить таблицу истинности для логического выражения
F = (A V B) /\ 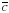
В данной функции три логические переменные – А, В, С
количество строк таблицы = 23 =8
количество логических операций равно 3 (, /\, V),
приоритет операций: действия в скобках (сложение), отрицание, умножение
количество столбцов таблицы = 3 + 3 = 6
рисуем таблицу и заполняем ее всевозможными наборами значений переменных:
| А | В | С |
|
|
|
| 0 | 0 | 0 |
|
|
|
| 0 | 0 | 1 |
|
|
|
| 0 | 1 | 0 |
|
|
|
| 0 | 1 | 1 |
|
|
|
| 1 | 0 | 0 |
|
|
|
| 1 | 0 | 1 |
|
|
|
| 1 | 1 | 0 |
|
|
|
| 1 | 1 | 1 |
|
|
|
Несложно заметить, что для функции от трех переменных данные наборы значений представляют собой двоичные триады, выписанные в порядке возрастания: 000, 001, 010, 011, 100, 101, 110, 111.
Для функции от трех и более переменных последовательность данных можно получить также следующим путем:
а) разделить колонку значений первой переменной пополам и заполнить верхнюю половину нулями, нижнюю половину единицами;
б) в следующей колонке для второй переменной половинку снова разделить пополам и заполнить группами нулей и единиц; аналогично заполнить вторую половинку;
в) так делать до тех пор, пока группы нулей и единиц не будут состоять из одного символа.
записываем в таблицу логические операции в порядке приоритета и заполняем столбцы результатами выполнения данных логических операций:
| А | В | С | A V B | 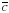
| (A V B) /\ 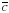 |
| 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 |
Основные законы и тождества алгебры логики
Тождества
| логического сложения | логического умножения |
| 1) А \/ 0 = А | 1) А /\ 0 = 0 |
| 2) А \/ 1 = 1 | 2) А /\1 = А |
| 3) А \/ А = А | 3) А /\ А = А |
| 4) А \/ 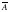 =1 (з –н исключенного третьего) =1 (з –н исключенного третьего) | 4) А /\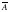 = 0 (з – н непротиворечия) = 0 (з – н непротиворечия) |
| 5) 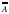 = А (двойное отрицание) = А (двойное отрицание) |
Законы алгебры логики
| Переместительный закон |
| 1) A V B = B V A | 1) A /\ B = B /\ A |
|
|
| Сочетательный закон |
| 2) (А V B) V C = A V (B V C) | 2) (А /\ B) /\ C = A /\ (B /\ C) |
|
|
| Распределительный закон |
| 3) (A \/ B) /\ C = A/\C \/ B/\C | 3) A/\B \/ C = (A \/ C) /\ (B \/ C) |
|
|
| Законы де Моргана (законы отрицания) |
| 4) 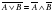 | 4) 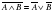 |
Основываясь на законах, можно выполнять упрощение сложных логических выражений.
Пример 1.
Упростить выражения (A B) B, (B C C), ( A C ) B C так, чтобы в полученных формулах не содержалось отрицания сложных высказываний.
(A B) B = A B B = A B
(B C C) = (B C) C = (B C) C = B C ( C C) = B C C = C (B 1) = C 1 = C
( A C) B C = A C B C = A C(1 B) = A C
Пример 2.
Упростить выражение: 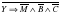
Решение:
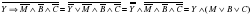
При упрощении выражения использовались формула замены операции импликации и закон де Моргана.
Решение логических задач
Алгоритм решения:
внимательно изучить условие задачи;
выделить простые высказывания и обозначить их латинскими буквами;
записать условие задачи на языке алгебры логики;
составить конечную формулу, для этого объединить логическим умножением формулы каждого утверждения. Приравнять произведение единице;
упростить формулу, проанализировать полученный результат или составить таблицу истинности. Найти по таблице значения переменных, для которых F =1, проанализировать результаты.
Задания ЕГЭ по теме «Логика»
1. /А12, 2004/. Какое логическое выражение равносильно выражению ¬ (А \/ ¬B)?
| 1) | A \/ B | 2) | A /\ B | 3) | ¬A \/ ¬B | 4) | ¬A /\ B |
Решение (вариант 1, использование законов де Моргана):
данное выражение представляет инверсию (отрицание) сложного высказывания, заданного в скобках. Раскроем скобки по закону де Моргана:
¬ (А \/ ¬B) = ¬А /\ ¬(¬B)
теперь воспользуемся законом двойного отрицания, по которому ¬(¬B) = В:
¬А /\ ¬(¬B) = ¬A /\ B
Ответ: 4
Решение (вариант 2, через таблицы истинности, если забыли формулы де Моргана):
Для доказательства равносильности логических выражений достаточно показать, что они принимают равные значения при всех возможных комбинациях исходных данных; поэтому можно составить таблицы истинности для исходного выражения и всех ответов и сравнить их:
| А | В | ¬А | ¬B | А ¬B | ¬ (А ¬B) | A B | A B | ¬A ¬B | ¬A B |
| 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 |
Очевидно, что таблицы истинности исходного выражения ¬ (А ¬B) и выражения ¬A B совпадают во всех строчках. Следовательно, правильный ответ – 4.
Ответ: 4
| Возможные проблемы: Необходимо знание построения таблиц истинности, в частности, приоритета выполнения логических операций. Сравнительно большой объем работы, особенно, если рассматривается выражение от трех и более переменных. |
2. /А10, 2005/. Укажите, какое логическое выражение равносильно выражению ¬ (¬А /\ B)
| 1) | A \/ ¬B | 2) | ¬A \/ B | 3) | B /\ ¬A | 4) | A /\ ¬B |
3. /А10, 2006/. Какое логическое выражение равносильно выражению ¬ (¬ A \/ B) \/ ¬C?
| 1) | (A /\ ¬B) \/ ¬C | 2) | ¬A \/ B \/ ¬C | 3) | A \/ ¬B \/ ¬C | 4) | (¬A /\ B) \/ ¬C |
4. /А10, 2007/. Какое логическое выражение равносильно выражению ¬ (A /\ B) /\ ¬C?
| 1) | ¬A \/ B \/ ¬C | 2) | (¬A \/ ¬B) /\ ¬C | 3) | (¬A \/ ¬B) /\ C | 4) | ¬A /\ ¬B /\ ¬C |
5. /А10, 2008/. Укажите, какое логическое выражение равносильно выражению
¬ (A \/ ¬ B \/ C).
| 1) | ¬A \/ B \/ ¬C | 2) | A /\ ¬B /\ C | 3) | ¬A \/ ¬B \/ ¬C | 4) | ¬A /\ B /\ ¬C |
Решение:
Воспользуемся законом де Моргана, применив его к трем логическим переменным, и тождеством двойного отрицания. Получим высказывание:
¬ (A \/ ¬ B \/ C) = ¬А /\ ¬ (¬B) /\ ¬C = ¬A /\ B /\ ¬C
Ответ: 4
6. /А8, 2009/. Укажите, какое логическое выражение равносильно выражению
A /\ ¬ (¬B \/ C).
| 1) | ¬A \/ ¬B \/ ¬C | 2) | A /\ ¬B /\ ¬C | 3) | A /\ B /\ ¬C | 4) | A /\ ¬B /\ C |
7. /А8, 2010/. Какое логическое выражение равносильно выражению
¬ (¬A \/ ¬B) /\ C?
| 1) | ¬A \/ B \/ ¬C | 2) | A /\ B /\ C | 3) | (A \/ B) /\ C | 4) | (¬A /\ ¬B) \/ ¬C |
8. /А8, 2010/. Какое логическое выражение равносильно выражению ¬ (¬A \/ B) /\ C ?
| 1) | (A \/ ¬B) /\ C | 2) | (¬A /\ B) \/ ¬C | 3) | A /\ ¬B /\ C | 4) | ¬A \/ ¬B \/ ¬C |
9. /А8, 2010/. Какое логическое выражение равносильно выражению ¬ (¬A /\ ¬B /\ C )?
| 1) | ¬A \/ ¬B \/ C | 2) | ¬A /\ ¬B /\ C | 3) | A \/ B \/ ¬C | 4) | A /\ B /\ ¬C |
10. /А8, 2010/. Укажите, какое логическое выражение равносильно выражению
¬ (¬B \/ ¬C) /\ ¬A.
| 1) | ¬A /\ (B /\ C) | 2) | ¬A /\ ¬B /\ C | 3) | ¬A \/ B \/ ¬C | 4) | ¬A /\ (B \/ C) |
11. /А13, 2004/. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
| X | Y | Z | F |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
Какое выражение соответствует F?
| 1) | ¬X/\¬Y/\Z | 2) | ¬X\/¬Y\/Z | 3) | X\/Y\/¬Z | 4) | X\/Y\/Z |
Решение (вариант 1, через таблицы истинности):
Чтобы решить данную задачу можно построить часть таблицы истинности для каждой из четырех функций, заданных в ответе для заданных наборов входных переменных, и сравнить полученные таблицы с исходной:
| X | Y | Z | F | ¬X | ¬Y | ¬Z | ¬X/\¬Y/\Z | ¬X\/¬Y\/Z | X\/Y\/¬Z | X\/Y\/Z |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
Очевидно, что значения заданной функции F совпадают со значениями выражения X\/Y\/¬Z. Следовательно, правильный ответ – 3.
Ответ: 3
| Возможные проблемы: Необходимо знание построения таблиц истинности, приоритета выполнения логических операций. Процесс это достаточно долгий и трудоемкий. |
Решение (Вариант 2):
Чтобы не строить таблицу истинности для каждого выражения, можно просто перепроверить предложенные ответы по заданной таблице истинности. Т.е. в каждую из четырех предложенных функций последовательно подставлять значения переменных X, Y и Z, из заданной таблицы истинности и вычислять значения логического выражения. Если значения вычисляемого выражения совпадут со значением F во всех трех строчках заданной таблицы, то это и есть искомое выражение.
Рассмотрим данный конкретный пример:
первое заданное выражение ¬X/\¬Y/\Z = 0 при X=0, Y=0, Z=0, что не соответствует первой строке таблицы;
второе заданное выражение ¬X\/¬Y\/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы;
третье выражение X\/Y\/¬Z соответствует F при всех предложенных комбинациях X,Y и Z;
четвертое выражение X\/Y\/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы.
Ответ: 3
| Возможные ловушки и проблемы: расчет на то, что ученик перепутает значки и в некоторых случаях заданные выражения-ответы лучше сначала упростить, особенно если они содержат импликацию или инверсию сложных выражений. |
12. /А11, 2005/. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
| X | Y | Z | F |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
Чему равно F?
| 1) | X/\Y/\Z | 2) | ¬X\/¬Y\/Z | 3) | X/\Y/\¬Z | 4) | ¬X/\¬Y/\¬Z |
13. /А11, 2006/. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
| X | Y | Z | F |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
Какое выражение соответствует F?
| 1) | ¬X \/ ¬Y \/ ¬Z | 2) | X /\ ¬Y /\ ¬Z | 3) | X \/ Y \/ Z | 4) | X /\ Y /\ Z |
14. /А11, 2007/. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
| X | Y | Z | F |
| 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 |
Какое выражение соответствует F?
| 1) | ¬X \/ Y \/ ¬Z | 2) | X /\ Y /\ ¬Z | 3) | ¬X /\ ¬Y /\ Z | 4) | X \/ ¬Y \/ Z |
15. /А11, 2008/. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов X, Y, Z.
| X | Y | Z | F |
| 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F?
| 1) | X \/ ¬Y \/ Z | 2) | X /\ Y /\ Z | 3) | X /\ Y /\ ¬Z | 4) | ¬X \/ Y \/ ¬Z |
16. /А9, 2009/. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
| X | Y | Z | F |
| 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Какое выражение соответствует F?
| 1) | ¬X /\ ¬Y /\ ¬Z | 2) | X /\ Y /\ Z | 3) | X \/ Y \/ Z | 4) | ¬X \/ ¬Y \/ ¬Z |
17. /А9, 2010/. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F:
| X | Y | Z | F |
| 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
Каким выражением может быть F?
| 1) | X /\ Y /\ Z | 2) | ¬X \/ ¬Y \/ Z | 3) | X \/ Y \/ Z | 4) | X /\ Y /\ ¬Z |
18. /А9, 2010/. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F:
| X | Y | Z | F |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Какое выражение соответствует F?
| 1) | X \/ Y \/ Z | 2) | X /\ Y /\ ¬Z | 3) | ¬X /\ Y /\ ¬Z | 4) | X \/ ¬Y \/ Z |
19. /А9, 2010/. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F:
| X | Y | Z | F |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 |
Какое выражение соответствует F?
| 1) | X \/ Y \/ Z | 2) | X /\ ¬Y /\ ¬Z | 3) | X \/ ¬Y \/ Z | 4) | ¬X /\ Y /\ ¬Z |
20. /А9, 2010/. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
| X | Y | Z | F |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Какое выражение соответствует F?
| 1) | ¬X \/ Y \/ ¬Z | 2) | ¬(X /\ Y /\ Z) | 3) | ¬X /\ ¬Y /\ Z | 4) | ¬(X \/ Y \/ Z) |
21. /А11, 2004/. Для какого имени истинно высказывание:
¬ (Первая буква имени гласная Четвертая буква имени согласная)?
| 1) | ЕЛЕНА | 2) | ВАДИМ | 3) | АНТОН | 4) | ФЕДОР |
Решение (вариант 1, используя свойства импликации):
Запишем логическую функцию, соответствующую данному высказыванию:
![]()
![]()
¬ (Первая буква имени гласная Четвертая буква имени согласная)
В
А
F(A, B) = ¬ (A B)
По условию задачи функция F(A, B) истинна, следовательно, отрицание этой функции – ложно, т.е. высказывание (A B) – ложно. Полученное высказывание является импликацией и ложно только в том случае, когда выражение А истинно, а В - ложно (см. табл. истинности импликации). Следовательно, среди предложенных ответов следует искать тот, в котором первая буква имени гласная и четвертая буква имени также гласная. Этому условию удовлетворяет только имя АНТОН.
Ответ: 3
| Возможные ловушки и проблемы: расчет на то, инверсия импликации может быть просто потеряна необходимо знание таблицы истинности импликации. |
Решение (вариант 2, преобразование данного выражения):
1) выражаем импликацию A B через базовые логические операции: A B = А В. Получаем выражение:
¬ (A B) = ¬(¬А В)
2) используя законы де Моргана и закон двойного отрицания, раскрываем скобки и упрощаем высказывание:
¬(¬А В) = ¬¬А ¬В = А ¬В
3) Так как, по условию задачи, заданное высказывание истинно, то А ¬В = 1. Данное логическое произведение истинно только если А – истинно и (¬В) – истинно, т.е. В – ложно. Следовательно, первая буква имени гласная и четвертая буква имени также гласная. Этому условию удовлетворяет только имя АНТОН.
Ответ: 3
22. /А7, 2010/. Какое из приведенных имен удовлетворяет логическому условию
¬ (первая буква гласная → вторая буква гласная) /\ последняя буква гласная
| 1) | ИРИНА | 2) | МАКСИМ | 3) | АРТЕМ | 4) | МАРИЯ |
Решение (способ 1):
Запишем логическую функцию, соответствующую данному высказыванию:
![]()
![]()
¬ (первая буква гласная → вторая буква гласная) /\ последняя буква гласная
В
А
F(A, B) = А /\ B
F(A, B) представляет собой конъюнцию (умножение) двух логических выражений. По условию задачи F(A, B) истинна, следовательно, высказывание А и высказывание В тоже должны быть истинны (см. табл. истинности конъюнкции).
Поскольку отрицание высказывания А истинно, значит, само высказывание А должно быть ложным. Высказывание А – это импликация, которая ложна лишь в одном случае, когда предпосылка истинна, а вывод ложный, т.е. высказывание {первая буква гласная} – истина, а высказывание {вторая буква гласная}- ложь. Поэтому, среди предложенных ответов следует искать тот, который удовлетворяет следующим условиям:
1) первая буква гласная,
2) вторая буква согласная,
3) последняя буква гласная.
Этому условию удовлетворяет только имя ИРИНА.
Ответ: 1
Решение (способ 2):
Пусть
А = «первая буква гласная»
В = «вторая буква гласная»
С = «последняя буква гласная»
Тогда заданное выражение можно представить в виде функции
F(A, B, C) = ¬ (A→ B) /\ C
Упростим данное выражение, используя представление импликации через базовые логические операции и логические законы:
F(A, B, C) = ¬ (A→ B) /\ C = ¬ (¬A B) C = (A ¬B) C = A ¬B C
Данная функция представляет собой конъюнкцию (умножение) трех логических выражений и, по условию задачи, она должна быть истинной, т.е.
A ¬B C = 1
Следовательно, А = 1, В = 0 (т.к. ¬B = 1), С = 1. Т.е. сформировалось следующее условие поиска: первая буква гласная, вторая буква согласная и последняя буква гласная.
Данному условию удовлетворяет только имя ИРИНА.
Ответ: 1
23. /А7 , 2010/. Для какого имени истинно высказывание:
Третья буква гласная (Первая буква согласная \/ В слове 4 гласных буквы)?
| 1) | Римма | 2) | Анатолий | 3) | Светлана | 4) | Дмитрий |
24. /А7 , 2010/. Какое из приведенных имен удовлетворяет логическому условию:
(вторая буква гласная первая буква гласная) /\ последняя буква согласная?
| 1) | АЛЕКСЕЙ | 2) | ПАВЕЛ | 3) | КСЕНИЯ | 4) | МАРИНА |
25. /А7 , 2010/. Какое из приведенных имен удовлетворяет логическому условию:
(первая буква гласная \/ первая буква согласная) вторая буква согласная?
| 1) | ИРИНА | 2) | КИРИЛЛ | 3) | ГАЛИНА | 4) | СЕРГЕЙ |
26. /А7 , 2010/. Для какого символьного набора истинно высказывание:
Вторая буква согласная /\ (В слове 3 гласных буквы \/ Первая буква согласная)?
| 1) | УББОШТ | 2) | ТУИОШШ | 3) | ШУБВОИ | 4) | ИТТРАО |
27. /А7 , 2010/. Для какого имени ложно высказывание:
(первая буква гласная /\ последняя буква согласная) (третья буква согласная?
| 1) | ДМИТРИЙ | 2) | АНТОН | 3) | ЕКАТЕРИНА | 4) | АНАТОЛИЙ |
28. /А7 , 2010/. Для какого из названий животных ложно высказывание:
Четвертая буква гласная (Вторая буква согласная?
| 1) | Собака | 2) | Жираф | 3) | Верблюд | 4) | Страус |
29. /А7 , 2010/. Какое из приведенных имен удовлетворяет логическому условию:
Первая буква гласная /\ Четвертая буква согласная \/ В слове четыре буквы?
| 1) | Сергей | 2) | Вадим | 3) | Антон | 4) | Илья |
30. /А9, 2005/. Для какого числа X истинно высказывание
X1 /\ ((X (X
Решение ( анализ исходного выражения и прямая подстановка):
Запишем логическую функцию, соответствующую данному высказыванию:
![]()
![]()
X1 /\ ((X (XF(A, B) = A /\ В – конъюнкция двух высказываний.
А
В
По условию задачи F(A, B) истинна, следовательно, выражения А и В тоже должны быть истинны (см. табл. истинности конъюнкции), т.е.
![]() X1 – истина
X1 – истина
((X (X
Рассмотрим предложенные ответы, подставляя значения Х в неравенства и проверяя истинность полученных высказываний:
1): 1 1 – ложь, что противоречит первому условию, т.е. ответ №1 не является решением задачи;
2): 2 1 – истина, первое условие совпадает,
(2 (2 (истина), что является истиной (см. табл. истинности импликации). Т. е. второе условие также совпадает;
3): 3 1 – истина, первое условие совпадает,
(3 (3 (ложь), что является ложью (см. табл. истинности импликации), это противоречит второму условию. Т.е. ответ №3 не является решением задачи;
4): 4 1 – истина, первое условие совпадает,
(4 (4 (ложь), что является ложью (см. табл. истинности импликации). Это противоречит второму условию, т.е. ответ №4 не является решением задачи.
Ответ: 2
31. /А9, 2006/. Для какого из указанных значений числа X истинно высказывание:
(X4) \/ ((X1) -(X4))?
Решение:
Запишем логическую функцию, соответствующую данному высказыванию:
(X4) \/ ((X1) -(X4)) т.е. F(A, B) = A \/ В – конъюнкция двух переменных.
![]()
![]()
А
В
F(A, B) истинна, если истинно хотя бы одно, входящее в нее высказывание (см. табл. истинности дизъюнкции). Поэтому решать данную задачу удобнее простой подстановкой предложенных ответов в логические высказывания А и В и определяя истинность полученных выражений:
1): 1 4 – ложь,
(1 1) (1 4) – истина;
2): 2 4 – ложь,
(2 1) (2 4) – ложь;
3): 3 4 – ложь,
(3 1) (3 4) – ложь;
4): 4 4 – ложь,
(4 1) (4 4) – ложь.
После рассмотрения всех вариантов видно, что правильным будет ответ под номером 1.
Ответ: 1
32. /А9, 2007/. Для какого числа X истинно высказывание
((X3) \/(X (X
Решение (анализ исходного выражения):
Запишем логическую функцию, соответствующую данному высказыванию:
((X3) \/ (X (XF(A, B) = A В – импликация двух переменных.
![]()
![]()
А
В
Очевидно, что в данной задаче высказывание В ложно для всех вариантов предложенных ответов. Тогда, согласно таблице истинности импликации, данная логическая функция F(A, B) будет истинной только в одном случае – если высказывание А ложно. Высказывание А, представляющее собой сумму двух высказываний, ложно только в том случае, если будут ложны оба входящих в нее высказывания, т.е. X3 – ложь и X
Ответ: 3
33. /А9, 2008/
Для какого из указанных значений числа X истинно высказывание
((X (X X (X
34. /А7, 2009/. Для какого из указанных значений X истинно высказывание
¬ ((X2) → (X3))?
35. /А7, 2010/. Для какого из указанных значений числа X истинно высказывание
((X (X X (X
36. /B2, 2004/ Укажите значения переменных K, L, M, N, при которых логическое выражение (¬K \/ M)-(¬L \/ M \/ N) ложно. Ответ запишите в виде строки из четырех символов: значений переменных K, L, M и N (в указанном порядке). Так, например, строка 1101 соответствует тому, что K=1, L=1, M=0, N=1.
Решение (вариант1, анализ исходного выражения):
Запишем логическую функцию, соответствующую данному высказыванию:
![]()
(¬K \/ M) (¬L \/ M \/ N) т.е. F(A, B) = A В – импликация двух высказываний.
![]()
В
А
Первый способ решения подходит для данной конкретной задачи, так как мы ищем ложное значение заданной функции.
F(A, B) представляет собой импликацию переменных А И В, и ложна тогда и только тогда, когда А – истинно, а В – ложно (по свойству импликации).
Рассмотрим высказывания А и В, представляющие собой дизъюнкцию нескольких переменных:
высказывание А истинно при (К, М) = (0,0), (0,1), (1,1);
высказывание В ложно лишь при (L, M, N) = (1,0,0) L=1, M=0, N=0. Но при таком значении переменной M возможно только К=0.
И поскольку ответ мы должны записать в виде строки из четырех символов, равных значениям переменных K, L, M, N, то получаем 0100 (Очень важно в ответе соблюсти заданный порядок переменных)
Ответ: 0100
Решение (вариант 2, преобразование заданного выражения):
Воспользуемся тождествами:
Получим:
(¬K \/ M) (¬L \/ M \/ N) = ¬ (¬K \/ M) \/ (¬L \/ M \/ N) = (K /\ ¬M) \/ (¬L \/ M \/ N)
По условию задачи (K /\ ¬M) \/ (¬L \/ M \/ N) = 0. Дизъюнкция равна нулю, если все, входящие в нее высказывания равны нулю. Следовательно, (¬L \/ M \/ N) = 0, но это выполняется лишь при L = 1, M = 0, N = 0.
Кроме того необходимо, чтобы K /\ ¬M =0, но при М = 0 (т.е ¬M =1) это достигается только для К = 0. Таким образом, получаем ответ: K = 0, L = 1, M = 0, N = 0.
Ответ: 0100
Решение (вариант 3, используя таблицы истинности):
Третий способ решения более громоздкий, но является универсальным для решения подобных задач. Можно построить таблицу истинности данной логической функции, используя тождественные преобразования или без них. И уже по таблице определить истинность или ложь заданного высказывания.
Построим таблицу истинности для функции F(K,L,M,N) =(¬K \/ M) (¬L \/ M \/ N), воспользовавшись алгоритмом построения таблиц истинности и свойствами логических операций. Получим
| K | L | M | N | ¬K | ¬K \/ M | ¬L | ¬L \/ M \/ N | F(K,L,M,N) |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
Из таблицы видно, что единственное ложное значение данная логическая функция принимает при K=0, L=1, M=0, N=0
Ответ: 0100
| Возможные проблемы: необходимо знать алгоритм построения таблиц истинности знать свойства и приоритет выполнения логических операций легко запутаться в многочисленных столбцах с однородными данными (нулями и единицами) достаточно долгий и трудоемкий процесс |
37. /B2, 2005/
Сколько различных решений имеет уравнение
(K/\L/\M)\/(¬L/\¬M/\N) = 1
где K, L, M, N - логические переменные?
В ответе не нужно перечислять все различные наборы значений K, L, M и N, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.
Решение (анализ данного выражения):
Запишем логическую функцию, соответствующую данному высказыванию:
![]()
![]()
(K/\L/\M) \/ (¬L/\¬M /\ N) т.е. F(A, B) = A \/ В - дизъюнкция двух высказываний
В
А
.Дизъюнкция A \/ В истинна в следующих случаях:
I. А=1 и В =0
II. В=1 и А =0
III. А=1 и В =1
Рассмотрим все три случая:
I. A = K /\ L /\ M =1 K=1, L=1, M=1 (по свойствам конъюнкции). Тогда B = (¬L/\¬M/\N) = ¬1 /\ ¬1 /\ N = 0 /\ 0/\ N =0 для любых значений N, т.е. N=1 или N=0.Следовательно, этот вариант дает 2 решения уравнения.
II. B = ¬L /\ ¬M /\ N =1 ¬L=1, ¬M=1, N=1 L=0, M=0, L=1. Тогда А = K /\ L /\ M = K /\ 0 /\ 0 = 0 для любых значений К. Следовательно, этот вариант также дает 2 решения уравнения.
III. Данный вариант не имеет решений, т.к. при А=1 высказывание В всегда равно нулю (см. вариант I).
Ответ: 4
38. /B2, 2006/. Укажите значения логических переменных K, L, M, N, при которых логическое выражение (K \/ M)-(M \/ ¬L \/ N) ложно.
Ответ запишите в виде строки из четырех символов: значений переменных K, L, M и N (в указанном порядке). Так, например, строка 0101 соответствует тому, что K=0, L=1, M=0, N=1.
39. /B2, 2008/. Сколько различных решений имеет уравнение
((K \/ L) – (L /\ M /\ N)) = 0
где K, L, M, N – логические переменные?
В ответе не нужно перечислять все различные наборы значений K, L, M и N, при которых выполнено данное равенство. В качестве ответа Вам нужно указать количество таких наборов
40. /B4, 2010/. Сколько различных решений имеет уравнение
J /\ ¬K /\ L /\ ¬M /\ (N \/ ¬N) = 0
где J, K, L, M, N – логические переменные?
В ответе не нужно перечислять все различные наборы значений J, K, L, M и N, при которых выполнено данное равенство. В качестве ответа Вам нужно указать количество таких наборов.
41. /B4, 2010/. Сколько различных решений имеет уравнение
¬M /\ K /\ ¬ N /\ ¬J /\ ( L \/ ¬L) = 0
где J, K, L, M, N – логические переменные?
В ответе не нужно перечислять все различные наборы значений J, K, L, M и N, при которых выполнено данное равенство. В качестве ответа Вам нужно указать количество таких наборов.
42. /B2, 2007/. Каково наибольшее целое число X, при котором истинно высказывание
(90X·X) – (X X -1))?
Решение (анализ данного выражения):
Рассмотрим (X X -1)). Очевидно, что это выражение будет ложным при любых положительных значениях Х.Тогда высказывание (90X·X) должно быть ложным, чтобы импликация была истинной. Наибольшее целое положительное значение Х, при котором высказывание (90X·X) ложно, равно 9.
Ответ: 9
43. /B4, 2009/. Каково наибольшее целое число X, при котором истинно высказывание
(50(X+1) ·(X+1))?
44. /B4, 2010/. Каково наименьшее натуральное число X, при котором истинно высказывание
(X · (X – 1) 80)?
Решение:
1). Рассмотрим случай, когда первая часть импликации ложна, т.е. (X · (X – 1) Наименьшее натуральное число X, при котором ложно данное высказывание – это Х = 11. Подставим полученное значение Х в левую и правую части импликации:
(11 · 10
(11 -1) · (11 – 1) 80 – истина.
Получаем: ложь истина = истина, т.е. при Х = 11 данное высказывание истинно.
2). Рассмотрим случай, когда первая часть импликации истинна, т.е. (X · (X – 1) Наименьшее натуральное число X, при котором истинно данное высказывание и, при этом, истинна вторая часть импликации – это Х = 10. Подставим полученное значение Х в левую и правую части импликации:
(10 · 9
(10 -1) · (10 – 1) 80 – истина.
Получаем: истина истина = истина, т.е. при Х = 10 данное высказывание тоже истинное.
По условию задачи необходимо выбрать наименьшее значение Х.
Ответ: Х = 10.
45. /B4, 2010/. Каково наибольшее целое число X, при котором ложно высказывание
(X · (X + 1) 55) → (X ·X 50)?
46. /B4, 2010/. Каково наибольшее целое число X, при котором истинно высказывание
(X · (X + 1) X·X + 7) → (X · (X + 1)
47. /B4, 2010/. Каково наименьшее натуральное число X, при котором ложно высказывание
(X·X – 7 15) → (X·X + 8
48. /B4, 2010/. Каково наибольшее целое число X, при котором ложно высказывание
(9X + 5 60) → (X ·X 80)?
49. /B4, 2010/. Каково наибольшее целое число X, при котором ложно высказывание
(8X - 6) 75) → (X · (X – 1) 65)?
50. /B4, 2010/. Каково наибольшее целое число X, при котором истинно высказывание
(X · X – 1 100) → (X · (X - 1) )?
51. /B4, 2005/. Мама, прибежавшая на звон разбившейся вазы, застала всех трех своих сыновей в совершенно невинных позах: Саша, Ваня и Коля делали вид, что происшедшее к ним не относится. Однако футбольный мяч среди осколков явно говорил об обратном.
‑ Кто это сделал? ‑ спросила мама.
‑ Коля не бил по мячу, ‑ сказал Саша. ‑ Это сделал Ваня.
Ваня ответил: ‑ Разбил Коля, Саша не играл в футбол дома.
‑ Так я и знала, что вы друг на дружку сваливать будете, ‑ рассердилась мама. ‑ Ну, а ты что скажешь? ‑ спросила она Колю.
‑ Не сердись, мамочка! Я знаю, что Ваня не мог этого сделать. А я сегодня еще не сделал уроки, ‑ сказал Коля.
Оказалось, что один из мальчиков оба раза солгал, а двое в каждом из своих заявлений говорили правду.
Кто разбил вазу?
Решение (способ 1, алгебраический, в соответствии с алгоритмом решения логических задач):
Обозначим высказывания:
А = «Коля разбил вазу»
В = «Ваня разбил вазу»
С = «Саша разбил вазу»
D = «Коля сегодня сделал уроки»
Согласно условию задачи, один из мальчиков солгал, а двое других говорили правду. Поэтому, если мы сложим записи истинного и ложного высказываний, составленных для каждого мальчика, то получим истинное высказывание.
Из слов Саши следует, что (А /\ B) \/ (А /\ B) истинно;
Из слов Вани следует, что (А /\ C) \/ (А /\ C) истинно;
Из слов Коли следует, что (В /\ D) \/ (В /\ D) истинно.
Следовательно, истинна и конъюнкция
((А /\ B) \/ (А /\ B)) /\ ((А /\ C) \/ (А /\ C)) /\ ((В /\ D) \/ (В /\ D)) = 1
Раскрывая скобки, получим:
((А /\ B) \/ (А /\ B)) /\ ((А /\ C) \/ (А /\ C)) /\ ((В /\ D) \/ (В /\ D)) =
(AB +AB) x (AC + AC) x (BD + BD) = (ABC + ABC) x (BD + BD) =


 ABCBD + ABCBD + ABCBD + ABCBD = ABCD + ABCD =
ABCBD + ABCBD + ABCBD + ABCBD = ABCD + ABCD =
0, (т.к. В/\В =0)
0
Ложь, по условию задачи
= ABCD = 1, следовательно, А=1. Т.е. Коля разбил вазу.
Ответ: Коля
| Возможные проблемы: необходимо уметь записывать условия задачи на языке алгебры логики преобразования хотя и простые, но длинные, поэтому можно легко запутаться в них, особенно в условиях стресса Необходимо знать законы преобразования логических выражений Требуется умение проанализировать полученный результат и отбросить заведомо противоречивые или не подходящие по условию задачи слагаемые (сомножители) в преобразованном выражении достаточно трудоемкий процесс |
Решение (способ 2):ответ ищется с помощью рассуждений.
Предположим, что Саша сказал правду: Коля не разбивал вазу, вазу разбил Ваня. Из двух оставшихся мальчиков кто-то дважды солгал. Допустим, Ваня тоже сказал правду: Коля разбил вазу, Саша вазу не разбивал. Но это противоречит словам Саши. Тогда допустим, что Ваня дважды солгал. Тогда получается, что Коля не разбивал вазы, а вазу разбил Саша. Но это снова противоречит словам Саши. Следовательно, дважды солгал именно Саша, а Ваня и Коля говорили правду, т.е. вазу разбил Коля.
Ответ: Коля
| Возможные проблемы: в этой задаче нет точной информации, поэтому приходится предполагать истинность того или другого высказывания и проверять, не противоречат ли этому предположению остальные утверждения необходимы навыки логического мышления |
52. /B4, 2006/. Три школьника, Миша (М), Коля (К) и Сергей (С), остававшиеся в классе на перемене, были вызваны к директору по поводу разбитого в это время окна в кабинете. На вопрос директора о том, кто это сделал, мальчики ответили следующее:
Миша: «Я не бил окно, и Коля тоже…»
Коля: «Миша не разбивал окно, это Сергей разбил футбольным мячом!»
Сергей: «Я не делал этого, стекло разбил Миша».
Стало известно, что один из ребят сказал чистую правду, второй в одной части заявления соврал, а другое его высказывание истинно, а третий оба факта исказил. Зная это, директор смог докопаться до истины.
Кто разбил стекло в классе? В ответе запишите только первую букву имени.
Решение 1: (используем метод рассуждений)
Предположим, что Миша сказал чистую правду: Миша не бил, Коля не бил, следовательно, бил Сергей. Тогда получается, то Коля также сказал чистую правду, что противоречит условию задачи. Следовательно, мальчики лгут.
Предположим, что полностью прав Сергей: Коля не бил, Сергей не бил, Миша бил. Тогда Миша соврал один раз, а Коля соврал дважды, что соответствует условию задачи.
Ответ: М
Решение 2 (составляем логические выражения):
Обозначим высказывания:
А = «Миша разбил окно»
В = «Коля разбил окно»
С = «Сергей разбил окно»
Согласно условию задачи, один из ребят сказал чистую правду, второй в одной части заявления соврал, а другое его высказывание истинно, а третий оба факта исказил. Запишем логические выражения в соответствии с высказываниями ребят и условиями задачи и упростим их, раскрыв скобки и используя логические законы и тождества:
Для Миши: (A /\ B) \/ (A /\ B) \/ ( A /\ B) = A \/ A /\B = 1
Для Коли: (A /\ C) \/ (A /\ C) \/ ( A /\ C) = A \/ A /\C = 1
Для Сергея: (C /\ A) \/ (C /\ A) = C/\A \/ C /\A = 1
Составим конъюнкцию данных высказываний, она так же должна быть истинной:
(A \/ A /\B) /\ (A \/ A /\C) /\ (C/\A \/ C /\A) = 1
Раскрывая скобки и используя логические законы и тождества, получаем
(A \/ A /\B) /\ (A \/ A /\C) /\ (C/\A \/ C /\A) = A/\C \/ A/\B/\C = A/\C /\ ( 1 \/ B) = A/\C =1. Следовательно, А=1, т.е. окно разбил Миша.
Ответ: М
53. По обвинению в ограблении перед судом предстали Иванов, Петров и Сидоров. Следствием установлено следующее:
1. Если Иванов невиновен или Петров виновен, то Сидоров виновен.
2. Если Иванов невиновен, то Сидоров невиновен.
Виновен ли Иванов? В ответе написать 1, если Иванов виновен, и 0 – если нет.
Решение (с помощью таблицы истинности)
Рассмотрим простые высказывания:
А = «Иванов виновен»;
В = «Петров виновен»;
С = «Сидоров виновен».
Запишем на языке алгебры логики факты, установленные следствием:
1. (¬А ۷ В) С
2. ¬А ¬С.
Составим единое логическое выражение для всех требований задачи.
Пусть F (A, ,B, C) = ((¬А ۷ В) С) ( ¬А ¬С).
Составим для данного высказывания таблицу истинности:
| A | B | C | ¬А | ¬А ۷ В | (¬А ۷ В) С | ¬С | ¬А ¬С | ((¬А ۷ В) С) (¬А ¬С) |
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
Из таблицы истинности видно, что в тех строчках, где сложное высказывание истинно, высказывание А - всегда истинно, т.е. Иванов виновен в ограблении.
Ответ: 1
| Возможные проблемы: необходимо уметь записывать условия задачи на языке алгебры логики знать правила построения таблиц истинности знать логические законы для преобразования сложных выражений требуется умение проанализировать полученный результат достаточно долгий и трудоемкий процесс |
54. /B4, 2007/. В школьном первенстве по настольному теннису в четверку лучших вошли девушки: Наташа, Маша, Люда и Рита. Самые горячие болельщики высказали свои предположения о распределении мест в дальнейших состязаниях.
Один считает, что первой будет Наташа, а Маша будет второй.
Другой болельщик на второе место прочит Люду, а Рита, по его мнению, займет четвертое место.
Третий любитель тенниса с ними не согласился. Он считает, что Рита займет третье место, а Наташа будет второй.
Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов.
Какое место на чемпионате заняли Наташа, Маша, Люда, Рита?
(В ответе перечислите подряд без пробелов числа, соответствующие местам девочек в указанном порядке имен.)
Решение (табличный метод):
Представим мнения болельщиков в таблице, учитывая, что каждый из них прав был только в одном из своих прогнозов. В данной таблице рассматривается случай, когда каждый из болельщиков бал прав в своем первом прогнозе:
| место | 1 | 2 | 3 | 4 |
| Болельщик |
|
|
|
|
| 1 | Наташа | Не Маша |
|
|
| 2 |
| Люда |
| Не Рита |
| 3 |
| Не Наташа | Рита |
|
| В итоге получилось | Наташа | Люда | Рита | Маша |
Если рассматривать любые другие сочетания высказываний, то будут получаться явные противоречия, когда одной и той же спортсменке присваиваются разные места или одно место дается разным спортсменкам.
Ответ: 1423
55. /B4, 2008/. Перед началом Турнира Четырех болельщики высказали следующие предположения по поводу своих кумиров:
А) Макс победит, Билл – второй;
В) Билл – третий, Ник – первый;
С) Макс – последний, а первый – Джон.
Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов.
Какое место на турнире заняли Джон, Ник, Билл, Макс?
(В ответе перечислите подряд без пробелов места участников в указанном порядке имен.)
56. В классе 36 человек. Ученики этого класса посещают математические, физический и химический кружки, причем математический кружок посещают 18 человек, физический - 14, химический - 10. Кроме того, известно, что 2 человека посещают все три кружка, 8 человек - и математический и физический, 5 - и математический и химический, 3 - и физический и химический.
Сколько учеников класса не посещают никаких кружков?
Решение (графический способ):
Для решения такого типа задач очень удобным и наглядным является использование кругов Эйлера.
Пусть самый большой круг изображает множество всех учеников класса, круги меньшего диаметра изображают множества членов математического, физического и химического кружков и обозначены буквами М, Ф, X. Поскольку все кружки посещают ученики одного класса, то круги меньшего диаметра будут располагаться внутри большого круга. Кроме того, они будут пересекаться, т.к. часть школьников посещает все три кружка. Изобразим это на рисунке:
Три пересекающихся круга образуют 7 непересекающихся областей, изображающих непересекающиеся подмножества учеников, каждый из которых посещает хотя бы 1 кружок.
Теперь обратимся к числовым данным.
![]()
В область 1) впишем число 2, так как все три кружка посещают 2 ученика. Далее известно, что ребят, посещающих и математический, и физический кружок, - 8. Но это множество является объединением множеств 1) и 2), причем в 1) входят 2 человека. Значит, на долю 2) остается 6 человек.
Теперь рассмотрим множество ребят, посещающих и математический, и химический кружок, состоящее из 5 человек. Оно также состоит из двух частей – 1) и 3), следовательно, на множество 3) приходится 3 человека (т.к. 5 – 2 = 3)
Рассмотрим теперь множество М, в которое входят 18 учеников. Оно состоит из четырех частей:1) +2) + 3) + 5). Количественный состав трех подмножеств мы уже нашли: это 2, 6 и 3. Значит, в четвертое подмножество, а именно в 5) , входит 18-(2 + 3 + 6) = 7 человек.
Аналогично определим количество учащихся в множествах 4), 6), 7).
Просуммируем цифры в этих областях: 6+5+7+3+2+1+4 = 28 человек посещает кружки.
Значит, 36 - 28 = 8 ребят не посещают никаких кружков.
Ответ: 8
| Возможные проблемы: изображая логические выражения в виде множеств, надо четко понимать , что конъюнкция (умножение) А В представляет собой пересечение множеств А и В, а дизъюнкция (сложение) А В – объединение данных множеств требуют внимания элементарные арифметические вычисления |
57. /B6, 2009/. Классный руководитель пожаловался директору, что у него в классе появилась компания из 3-х учеников, один из которых всегда говорит правду, другой всегда лжет, а третий говорит через раз то ложь, то правду. Директор знает, что их зовут Коля, Саша и Миша, но не знает, кто из них правдив, а кто – нет. Однажды все трое прогуляли урок астрономии. Директор знает, что никогда раньше никто из них не прогуливал астрономию. Он вызвал всех троих в кабинет и поговорил с мальчиками. Коля сказал: "Я всегда прогуливаю астрономию. Не верьте тому, что скажет Саша". Саша сказал: "Это был мой первый прогул этого предмета". Миша сказал: "Все, что говорит Коля, – правда". Директор понял, кто из них кто. Расположите первые буквы имен мальчиков в порядке: "говорит всегда правду", "всегда лжет", "говорит правду через раз". (Пример: если бы имена мальчиков были Рома, Толя и Вася, ответ мог бы быть: РТВ)
58. /B6, 2010/. На одной улице стоят в ряд 4 дома, в которых живут 4 человека: Алексей, Егор, Виктор и Михаил. Известно, что каждый из них владеет ровно одной из следующих профессий: Токарь, Столяр, Хирург и Окулист, но неизвестно, кто какой и неизвестно, кто в каком доме живет. Однако, известно, что:
1) Токарь живет левее Столяра
2) Хирург живет правее Окулиста
3) Окулист живет рядом со Столяром
4) Токарь живет не рядом со Столяром
5) Виктор живет правее Окулиста
6) Михаил не Токарь
7) Егор живет рядом со Столяром
8) Виктор живет левее Егора
Выясните, кто какой профессии, и кто где живет, и дайте ответ в виде заглавных букв имени людей, в порядке слева направо. Например, если бы в домах жили (слева направо) Константин, Николай, Роман и Олег, ответ был бы: КНРО
59. /B6, 2010/ На олимпиаде по информатике участвовало пятеро учеников: Вася (В), Гриша (Г), Иван (И), Саша (С), Юра (Ю). Об итогах олимпиады имеется пять высказываний:
а) Выиграл Вася, а Юра поднялся на второе место.
б) Саша занял только второе место, а Вася был последним.
в) Второе место занял Иван, а Гриша оказался третьим.
г) На первом месте был Гриша, а Юра был четвертым.
д) Юра был четвертым, а Иван вторым.
Если известно, что в каждом высказывании одно утверждение верное, а другое нет, то кто занял второе место и на каком месте был Иван?
Ответ запишите в виде первой буквы имени второго призера и, через запятую, номер места, занятого Иваном.
60. /B6, 2010/. Директору доложили, что в школе появилась компания из 3-х учеников, один из которых всегда говорит правду, другой всегда лжет, а третий говорит через раз то ложь, то правду. Директор знает, что их зовут Коля, Саша и Миша, но не знает, кто из них правдив, а кто - нет. Однажды все трое (каждый в первый раз) прогуляли урок труда. При разговоре с директором Коля сказал: «Я всегда лгу». Миша сказал: «Коля прав». Директор понял, кто из них кто. Расположите первые буквы имен мальчиков в порядке: «говорит всегда правду», «всегда лжет», «говорит правду через раз». Например, если бы имена мальчиков были Александр, Руслан и Олег, ответ был бы: АРО.
Ответы к заданиям:
| № задания | Ответ | № задания | Ответ | № задания | Ответ | № задания | Ответ |
| 1 | 4 | 16 | 4 | 31 | 1 | 46 | 7 |
| 2 | 1 | 17 | 3 | 32 | 3 | 47 | 6 |
| 3 | 1 | 18 | 1 | 33 | 2 | 48 | 8 |
| 4 | 2 | 19 | 3 | 34 | 3 | 49 | 8 |
| 5 | 4 | 20 | 1 | 35 | 4 | 50 | 10 |
| 6 | 3 | 21 | 3 | 36 | 0100 | 51 | Коля |
| 7 | 2 | 22 | 1 | 37 | 4 | 52 | М |
| 8 | 3 | 23 | 1 | 38 | 1100 | 53 | 1 |
| 9 | 3 | 24 | 1 | 39 | 10 | 54 | 1423 |
| 10 | 4 | 25 | 1 | 40 | 30 | 55 | 3124 |
| 11 | 3 | 26 | 4 | 41 | 30 | 56 | 8 |
| 12 | 4 | 27 | 2 | 42 | 9 | 57 | СКМ |
| 13 | 3 | 28 | 4 | 43 | 7 | 58 | АМВЕ |
| 14 | 2 | 29 | 4 | 44 | 10 | 59 | С,5 |
| 15 | 1 | 30 | 2 | 45 | 7 | 60 | СМК |


 Получите свидетельство
Получите свидетельство Вход
Вход


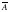 , not
, not

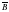 ) /\ (
) /\ (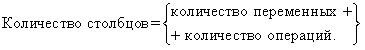
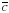
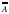 = А (двойное отрицание)
= А (двойное отрицание)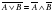
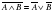
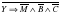
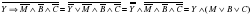









 Сборник материалов и тренировочных заданий ЕГЭ по информатике (0.13 MB)
Сборник материалов и тренировочных заданий ЕГЭ по информатике (0.13 MB)
 0
0 1102
1102 87
87 Нравится
0
Нравится
0









