Решение задач олимпиадного уровня 9 класс

Задания школьного этапа олимпиады

школьников по физике в 2019 - 2020 учебном году

9 класс

Задача 1 Саша, Коля и Дима приняли участие в соревнованиях по бегу на дистанцию L = 200 м. На старте друзья располагались на соседних дорожках. Саша, стартовавший на первой дорожке, финишировал первым через t = 40 с, а Дима на третьей дорожке отстал от победителя на Δt = 10 с. Определите скорость Коли на второй дорожке, если известно, что в момент финиша Саши все три бегуна располагались на одной прямой. Скорости бега спортсменов можно считать постоянными на всей дистанции, а беговую дорожку прямой. Задача 2 Система, состоящая из двух однородных стержней разной плотности, находится в равновесии. Масса верхнего стержня m₁ = 3,6 кг. Трение пренебрежимо мало. Определите, при какой массе m₂ нижнего стержня возможно такое равновесие.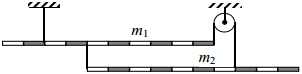 Задача 3 Тело, привязанное нитью ко дну сосуда, погружено в жидкость на 2/3 своего объёма. Сила натяжения нити при этом равна T₁ = 12 Н. Для того чтобы вынуть это тело из жидкости на 2/3 объёма, нужно отвязать тело ото дна и приложить к нему сверху направленную вертикально вверх силу T₂ = 9 Н. Определите отношение плотностей жидкости и тела. 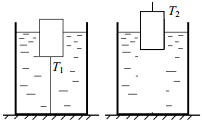Задача 4 Для поддержания в доме постоянной температуры T = +20 ºС в печку всё время подкладывают дрова. При похолодании температура воздуха на улице понижается на Δt = 15 ºС, и для поддержания в доме прежней температуры приходится подкладывать дрова в 1,5 раза чаще. Определите температуру воздуха на улице при похолодании. Какая температура установилась бы в доме, если бы дрова подкладывали с прежней частотой? Считайте, что мощность передачи теплоты от комнаты к улице пропорциональна разности их температур.

Решение школьного этапа олимпиады

школьников по физике в 2019 - 2020 учебном году

9 класс.

Решение к первой

Найдём скорость Саши: V₁ = L/t  и скорость Димы: V₃ = L/(t + Δt)

В момент времени t Дима отстал от Саши на расстояние Δl = (V₁ – V₃)t.

Из того, что все три друга в этот момент находились на одной прямой, следует, что Коля отстал от Саши на расстояние Δl/2. С другой стороны Δl/2 = (V₁ – V₂)t, где V₂ – скорость Коли. Решая записанную систему уравнений, получим: ÷

Критерии оценивания

• Найдены скорости Саши и Димы (по 1 баллу за каждую): 2 балла

• Найдено расстояние, на которое Дима отстал от Саши в момент времени t: 2 балла

• Использовано, что друзья расположены на одной прямой, и получена связь между расстояниями, на которые Дима и Коля отстали от Саши: 2 балла

• Записано выражение для расстояния, на которое Коля отстал от Саши в момент времени t, через скорость Коли: 2 балла

• Получено выражение для скорости Коли: 1 балл

• Получено численное значение скорости Коли: 1 балл

Максимум за задачу – 10 баллов.

Решение ко второй

Запишем уравнение моментов для нижнего стержня относительно его центра тяжести: 5T₁ – 2T₂ = 0, где T₁  – сила реакции со стороны левой нити, T₂  – сила реакции со стороны правой нити.

Условие равновесия нижнего стержня:

T₁ + T₂ = m₂g

Из этих двух уравнений находим:

T₁ = 2/7 *m₂g,

– T₂ = 5/7*m₂g.

Запишем уравнение моментов для верхнего стержня относительно точки крепления левой (верхней) нити:

Критерии оценивания

• 5T₁ – 2T₂ = 0: 2 балла

• T₁ + T₂ = m₂g: 1 балл

• T₁ = 2/7*m₂g и T₂ = 5/7m₂g (по 1 баллу за каждую силу): 2 балла

• Уравнение моментов: 4 балла

• m₂ = 2.1 кг: 1 балл

Максимум за задачу – 10 баллов.

Решение к третьей

Запишем условие равновесия тела в первом случае:

где ρ_Т – плотность тела, ρ_Ж – плотность жидкости, ܸV– объём тела.

Условие равновесия тела во втором случае:

Поделим одно уравнение на другое:

Критерии оценивания

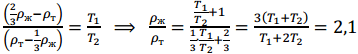
• Сила Архимеда в виде ρ_Ж gV_погр: 1 балл

• Условие равновесия тела в первом случае : 4 балла

• Условие равновесия тела во втором случае : 4 балла

• ρ_Ж/ρ_T = 2.1: 1 балл

Максимум за задачу – 10 баллов

Решение к четвертой

Пусть температура воздуха на улице до похолодания была равна ,ݐа епловая мощность, поступающая в дом за счёт сжигания дров, была равна P. Тогда до похолодания:

P = α(T – t)

где α – некоторый постоянный коэффициент пропорциональности.

После похолодания:

1,5ܲP = α(T – (t – Δt))

Поделим одно уравнение на другое:

 

Если бы дрова подкладывали с прежней частотой, то:

 

Критерии оценивания

• P = α(T – t): 3 балла

• 1,5P = α(T – (t – ∆t)): 3 балла

• t – ∆t = – 25°C: 1 балл

• T‘ = 5°C: 3 балла

Максимум за задачу – 10 баллов.