Решение задач на движение заряженной частицы в магнитном поле

1.Образовательная задача

• проверка знания закона Лоренца и правила левой руки; основных формул по теме «Магнитное поле» и единиц измерения электродинамических величин;

• доведение до автоматизма навыков определения направления действия силы Лоренца по правилу левой руки; определения формы траектории заряженной частицы; расчета радиуса орбиты, периода обращения частицы и шага спирали;

• владение навыками и приемами письменной и устной, монологической и диалогической речи ( анализ решения задачи); проверка знаний алгоритма решения задач на движение частицы в магнитном поле.

2. Воспитательная задача.

• формирование представлений о влиянии условий (направления скорости) на характер протекания явления (траекторию движения).

• развитие умения работать индивидуально у доски и в тетради; аккуратно вести записи, общаться с одноклассниками и педагогом.

3. Развивающие задачи.

• развитие речи, мышления, сенсорики; воспитание чувства сопереживания, доброжелательности;

• развитие умений анализировать условие задачи, предсказывать результаты, делать выводы, стоить план решения задачи.

1.Актуализация опорных знаний

1. Проверка основных формул (дописать пропущенные физические величины)

В= F/I… ; Fл= eB…sinα; A= …U; B= μ₀μN…/ℓ; T=2π…/υ; E=F/…; Fa=B……sinα; F=mац=m…/r.

1. Проверка единиц измерения физических величин:

Тл= Н/А_*м; В= Дж/Кл; Гн= В_*с/А; Н= кг_* м/с²; Кл=А_*с; Дж=Н_*м; Вб=Тл_*м²

Εi F I Ф

q L A B

2. Проверка правила левой руки.

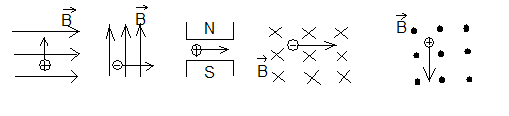
4. Фронтальный опрос.

1) Как называется сила, с которой магнитное поле действует на заряженную частицу?

2) От чего зависит модуль силы Лоренца?

3) Как рассчитать модуль Fл?

4) Как определяется направление Fл? Сформулировать?

5) Изменяется ли модуль скорости в магнитном поле? Ее направление?

6) Как будет двигаться частица, если υ║B?

7) Как будет двигаться частица, если υ_┴B?

8) Какой будет траектория, если 0°

9) Как поступают, если υ под углом α к В?

10) Как влияет υ║ на движение частицы?

11) Как влияет υ_┴ на движение частицы?

12) Какой будет траектория?

2. Решение задач

1) В направлении, перпендикулярном линиям индукции в магнитное поле влетает электрон со скоростью 10 Мм/с, окружность какого радиуса описал электрон, если индукция поля 10мТл?

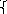
В =10мТл 10_*10^-3 Тл Fл=еυВ [r=кг_*м/Кл_*с_*Тл=кг_*м_*А_*м/А_*с_*с_*Н=м] υ=10Мм/с 10_*10⁶ м/с Fл=mυ/r r=9,1_*10^-31_*10⁷ /1,6_*10^-19_*10^-2 =5,7_*10^-3 м.

е= 1,6_*10^-19 Кл eυB=mυ²/r

m = 9,1_*10^-31 кг r=mυ²/eυB=mυ/eB

r-?

2) Чему равен период обращения электрона по окружности?

Т=2πr/υ=2πmυ/υeB=2πm/eB. [T=кг/Кл_* Тл=кг_*А_*м/А_*с_*Н=с]

Т=2_*3,14_*9,1_*10^-31 /1,6_*10^-19_*10^-2 = 36_*10^-10 с.

Изменится ли сила Лоренца, если в магнитное поле на тех же условиях влетит протон? Будет ли он двигаться по такой же окружности? С таким же периодом?

3) Электрон влетает в однородное магнитное поле с индукцией 5 мТл со скоростью 10 Мм/с под углом 30° к вектору индукции. Определить шаг спирали, по которой будет двигаться электрон.

В =5мТл 5_*10^-3 Тл υ_║= υ_*cosα

υ=10Мм/с 10_*10^-6 м/с υ_┴= υ_*sinα

α =60° h= υ_║T= υ_*cosα_*T (1)

h-? T=2πr/υ_┴=2πr/υ_* sinα (2)

m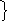 =9,1_*10^-3 кг Fл=eυBsinα eυBsinα= mυ² sin²α/r

e=1,6_*10^-19Кл F=mυ_┴² /r= mυ² sin²α/r r=mυsinα/eB (3)

(3) во (2)

T=2πmυsinα/υsinαeB=2πm/eB (4)

(4) в (1)

h=υcosα_*2πm/eB=2πυmcosα/eB

[h=кг_* м/с_* Кл_*Тл=кг_*м_*А_*м/с_*А_*с_*Н= м]

h=2_*3,14_*9,1_*10^-31_* 10⁷ /1,6_*10^-19_*5_*10^-3_*2=3,6_*10^-9 м.

Измениться ли шаг спирали, если в магнитное поле влетает протон? А если магнитное поле будет однородным?

Усложним задачу. Рассмотрим движение частицы в электромагнитном поле.

Для начала вспомним, какое влияние оказывает эл. поле на заряженную частицу.

4) Электрон влетает со скоростью υ₀ под углом α

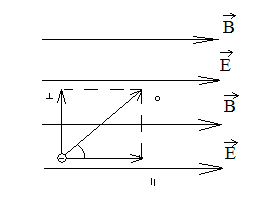
υ ₀ υ_0║ = υ_0*cosα N= t/T (1) (4) в (3)

α_0┴= υ_0*sinα υ= υ_0║- at T=2πmυ₀sinα/υ₀sinαeB=2πm/eB(5)

Е 0= υ_0║- at (3) во (2)

В t= υ_0║/a= υ_0*cosα/a (2) t= υ_0*cosαm/eE (6)

ma= eE (6) и (5) в (1)

N-? a= eE/m (3) N= υ_0*cosαm_*eB/eE_*2πm

T= 2πr/ υ_0┴= 2πr/ υ_0*sinα (3)

mυ_┴/r= eυ_┴*B (4) N= υ_0*cosα_*B/ 2πE

[N= м_*Тл_*Кл/ с_*Н= м_*Н_*А_*с= 1]

Что измениться, если в это поле попадет протон?

3. Определение алгоритма решения задачи.

1. Сделать чертеж.

2. Указать силовые линии магнитного поля ( электрического поля)

3. Проставить вектор υ₀ , разложить его на составляющие.

4. Определить вид траектории.

5. Составить основное уравнение динамики

с учетом сил, действующих на частицу.

Задание: По чертежам определить, к какому типу( 1, 2, 3) относится задача.

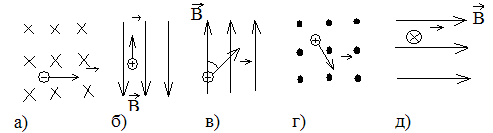
С амостоятельно: B= 10мТл

α = 45°

υ= 5 Мм/с

1. F_л- ?

2. r- ?

3. Т- ?

4. Применение силы Лоренца.

1) Ускорение заряженных частиц.

2) Управление электронным пучком.

3) Определение удельного заряда и масс частиц.

4) Магнитные ловушки (удерживание частицы в заданном объеме).

5. Задание на дом:

6. Подведение итогов урока.

4