Решение нестандартных задач по математике как средство формирования учебной мотивации

Решение нестандартных задач по математике как средство формирования учебной мотивации

Учитель начальных классов:

Готка Н.Н.

Ⅱ кв.категория

МОУ «ТСШ № 15»

Учение, лишённое всякого интереса и взятое 

только силой принуждения, убивает в ученике 

охоту к овладению знаниями. 

Приохотить ребёнка к учению гораздо более достойная задача, чем приневолить.

К.Д. Ушинский. .

Нестандартная задача – это задача, для решения которой, как правило, требуется нестандартное мышление, сообразительность, использование мыслительных операций.

Виды нестандартных задач по программе «Школа России»,

автор М. И. Моро:

1.задачи на соответствие;

2.комбинаторные задачи;

3.логические задачи;

4.задачи на вместимость;

5.задачи на взвешивание;

6.теория вероятности;

7.«магический квадрат»;

8. головоломки;

9.«занимательные рамки».

Комбинаторные задачи - это задачи, требующие осуществления перебора всех возможных вариантов или подсчёта их числа.

Методы решения комбинаторных задач:

-метод перебора;

-табличный метод;

-построение дерева решений;

-построение графов;

-использование комбинаторного правила умножения.

Метод перебора возможных вариантов

Задача 1. Для своих двух книг Маша купила три разные обложки.

Сколькими различными способами она может обернуть книги купленными обложками?

а

в

б

Составим из букв всевозможные пары:

аб, ав, бв, ба, ва, вб.

Всего получилось 6 способов .

Табличный метод

Задача 2. Маша, Оля, Вера, Ира, Андрей, Миша и Игорь готовились стать ведущими на Новогоднем празднике. Назовите возможные варианты, если ведущими могут быть только одна девочка и один мальчик.

Решение. Составим таблицу: слева первый столбец - имена девочек, вверху первая строка - имена мальчиков .

Андрей

Маша

Миша

Оля

Миша-Андрей

Вера

Игорь

Маша-Миша

Оля-Андрей

Ира

Оля-Миша

Вера-Андрей

Маша-Игорь

Вера-Миша

Оля-Игорь

Ира-Андрей

Вера-Игорь

Ира-Миша

Ира-Игорь

Ответ: Все возможные варианты перечисляются в строках и столбцах таблицы. Всего 12 вариантов .

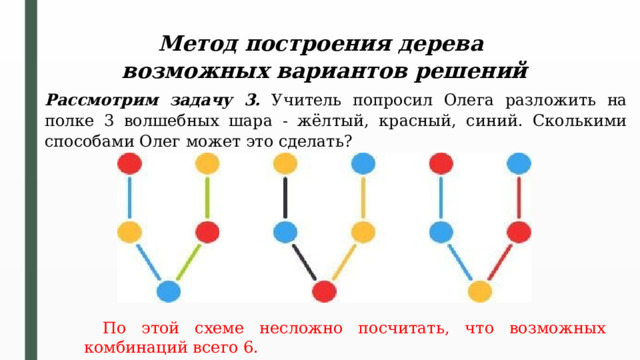
Метод построения дерева

возможных вариантов решений

Рассмотрим задачу 3. Учитель попросил Олега разложить на полке 3 волшебных шара - жёлтый, красный, синий. Сколькими способами Олег может это сделать?

По этой схеме несложно посчитать, что возможных комбинаций всего 6.

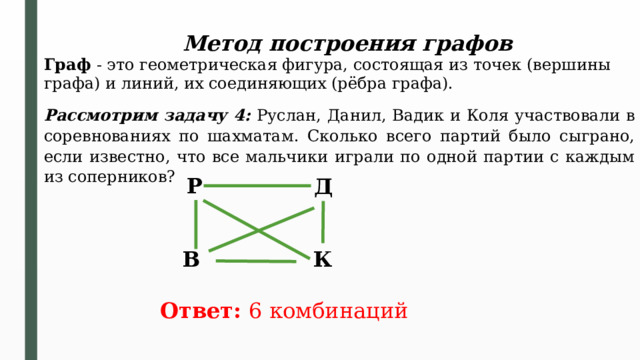
Метод построения графов

Граф - это геометрическая фигура, состоящая из точек (вершины графа) и линий, их соединяющих (рёбра графа).

Рассмотрим задачу 4: Руслан, Данил, Вадик и Коля участвовали в соревнованиях по шахматам. Сколько всего партий было сыграно, если известно, что все мальчики играли по одной партии с каждым из соперников?

Р

Д

В

К

Ответ: 6 комбинаций

Использование комбинаторного правила умножения

Решим такую задачу 5: Мартышка, Осёл, Козёл и Мишка пересаживались, считая, что от этого зависит звучание музыки. Сколькими способами они могли пересесть?

Мишка-1

Мартышка-4

Осёл-3

Козёл-2

Решение: 4 ∙3 ∙ 2 ∙ 1 =24 способа

Нестандартные задачи являются источником развития умственных способностей учащихся, развивают критическое мышление, дерзость ума, формируют интерес к самостоятельной деятельности, повышают положительную мотивацию к изучению математики и другим дисциплинам.

Спасибо за внимание!