Получите свидетельство
Вход
Урок алгебры в 9 классе
Тема: « Решение
неравенств
методом
интервалов »
1) Является ли данное число а решением данного неравенства 2-6х
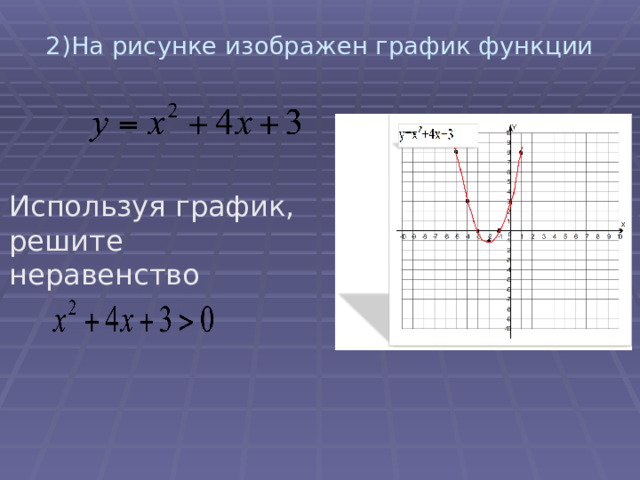
2)На рисунке изображен график функции
Используя график, решите неравенство
1)
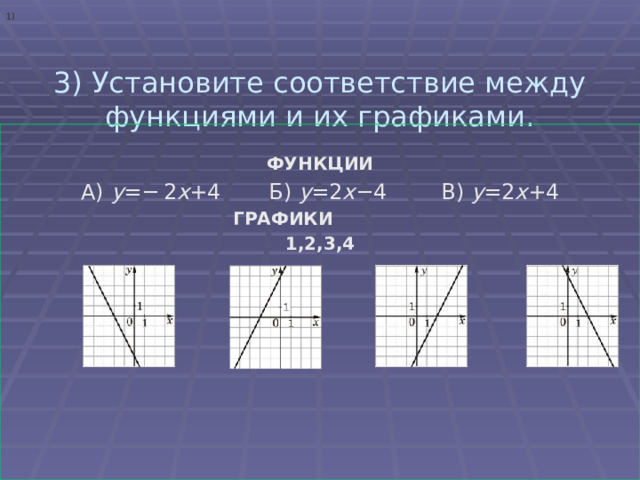
3) Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) y =− 2 x +4 Б) y =2 x −4 В) y =2 x +4
ГРАФИКИ
1,2,3,4
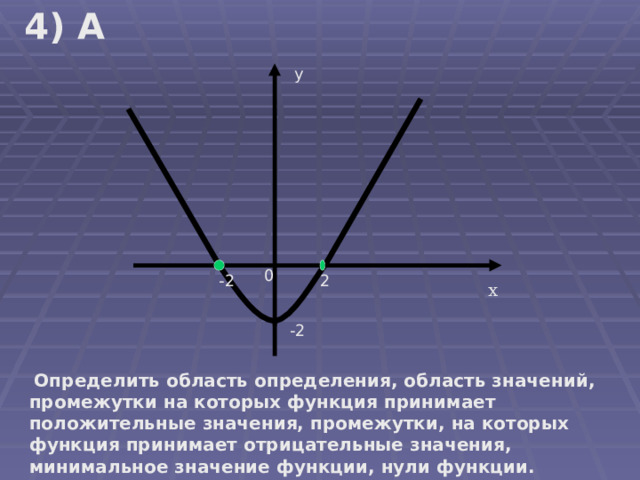
4) А
у
0
2
-2
х
-2
Определить область определения, область значений, промежутки на которых функция принимает положительные значения, промежутки, на которых функция принимает отрицательные значения, минимальное значение функции, нули функции.
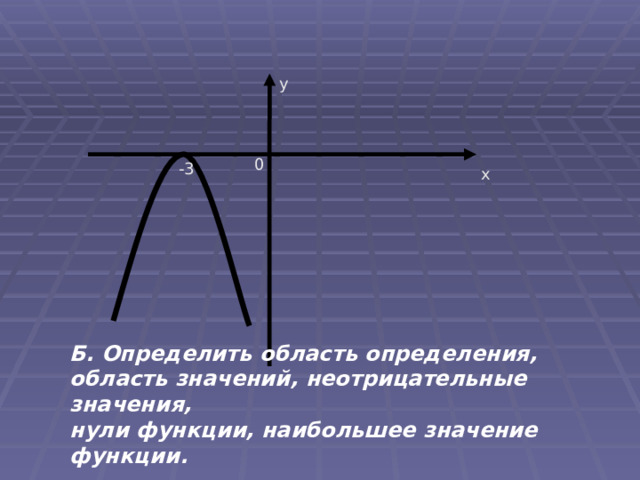
у
0
-3
х
Б. Определить область определения,
область значений, неотрицательные значения,
нули функции, наибольшее значение функции.
Решить неравенство
1) (х+2)(х+4)(х-1)
f(х)=(х+2)(х+4)(х-1)
х=-4 х=-2 х=1
Ответ: (-∞;-4) È (-2;1)
Решить неравенство Что называется областью определения?
Решение: равносильно: (х-5)(х+6)
- Рассмотрим функцию f(х)=(х-5)(х+6)
- Нули функции х=5, х=-6
Ответ: (-6;5).
![Решить неравенство 2)У = (х+12)(х-1)(х-9)≥0 (-∞ Ответ: [-12;1] È [9;+ ¥ ).](https://fsd.videouroki.net/html/2024/03/29/v_66066bdc80e71/img10.jpg)
Решить неравенство
2)У =
(х+12)(х-1)(х-9)≥0
(-∞
Ответ: [-12;1] È [9;+ ¥ ).
![Работа по учебнику Решить № 2.16.(а,г) Решение: а)Неравенство (х 2 -4)/(х 2 -9)≥0 равносильно:(х 2 -4)(х 2 -9)≥0; х=2; х=-2; х=-3; х=3 б) Неравенство х(х 2 -16)/(х 2 -9)≤0 равносильно х(х-4)(х+4)(х-3)(х+3)≤0 Ответ: а)(-∞;-3] ᴗ[-2;2] ᴗ[3;∞) г) (-∞;-4]ᴗ [-3;0]ᴗ[3;4]](https://fsd.videouroki.net/html/2024/03/29/v_66066bdc80e71/img11.jpg)
Работа по учебнику
- Решить № 2.16.(а,г)
Решение: а)Неравенство (х 2 -4)/(х 2 -9)≥0 равносильно:(х 2 -4)(х 2 -9)≥0; х=2; х=-2; х=-3; х=3
б) Неравенство х(х 2 -16)/(х 2 -9)≤0 равносильно
х(х-4)(х+4)(х-3)(х+3)≤0
Ответ: а)(-∞;-3] ᴗ[-2;2] ᴗ[3;∞)
г) (-∞;-4]ᴗ [-3;0]ᴗ[3;4]
0. в) х 2 -14х+33 ≤ 0 " width="640"
1.Найти область определения функции:
- 1 вариант 2 вариант
- у= у=
2.Решить неравенство методом интервалов:
вариант 2 вариант
а)(х+5)(6-х) ≥ 0; а)(х+6)(х=2 )
б)х 2
в)2х 2 -9х+4 0. в) х 2 -14х+33 ≤ 0
- Домашнее задание
- п.2, на оценку "3"-№2.20(а,б);2.21(а)
- на оцеку "4"-№2.21(б); 2.22(а,б)
- на оценку "5"- 2.22(в); 2.31
Спасибо за урок
Решение неравенств методом интервалов (2.31 MB)
0
54
2
Нравится
0
