Рекомендации по решению упражнений

1. Найти период функции

у=cos2x+ctg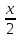

Решение

Первое слагаемое можно записать в виде cos2x=cos(2x+2π)=cos(2(x+π)), поэтому его период равен π: Т₁=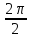=π.

Второе слагаемое можно записать в виде ctg 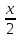=ctg (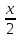+π)= ctg 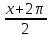, поэтому его период равен 2π: Т₂= 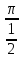=2π.

Периодом данной функции будет наименьшее общее кратное (НОК) периодов слагаемых, т.е. Т= 2 π.

Ответ: 2π.

1. Решить уравнение 3^у=1, где у=х²-5х+6

Решение

Представим правую часть уравнения в виде степени 3:

3^у=3⁰.

Сравним показатели степеней в левой и правой частях:

х²-5х+6=0;

х₁=2; х₂=3.

Проверка

Если х₁=2, то левая часть 3 ^4-10+6=3⁰, а правая 1=3⁰.

Следовательно, х₁=2, х₂=3.

Ответ : 2; 3.

3) Доказать тождество

(а+b)²+(а-b)²=2(a²+b²)

Доказательство

Преобразуем левую часть равенства, применяя формулы сокращенного умножения:квадрат суммы и квадрат разности

(а+b)²+(а-b)²=a²+2ab+b²+a²-2ab+b²=2a²+2b²=2(a²+b²)

2(a²+b²)= 2(a²+b²),

что и требовалось доказать

4) Катер, развивающий в стоячей воде скорость 20 км/ч, прошел 36 км против течения и 22 км по течению, затратив на весь путь 3 ч.

Найти скорость течения реки.

Решение

Задача решается с помощью рационального уравнения.

Пусть х км/ч – скорость течения реки. Тогда скорость катера против течения (20-х) км/ч, а по течению (20+х) км/ч.

Против течения реки 36 км катер прошел за 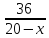ч, а по течению реки за 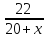ч.

Значит время, затраченное на весь путь равно

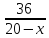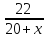( +) ч.

По условию задачи на весь путь катер затратил 3 ч.

Следовательно, 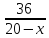+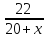=3.

Решив это уравнение, найдем его корни : х₁=- 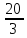; х₂=2.

Смыслу задачи не удовлетворяет первый корень и удовлетворяет второй.

Ответ : 2 км/ч.

5) Решить неравенство lg²x+2lgx

Решение

Областью определения неизвестного является x0.

Обозначим у=lgx, тогда у²=lg²x, получаем y²+2y-3

Отсюда -3ylgx

Следовательно, 0,001x

Ответ: (0,001; 0,1).