Цели урока:
- Познакомить учащихся со способами решения показательных уравнений и неравенств.
- Развивать навыки решения, продолжить работу над формированием способностей к самостоятельному анализу и синтезу.
- Воспитывать ответственность
Ход урока:
1. Организационный момент.
Снежки
Учитель объявляет тему и цель урока, что отражено в записях на доске.
2. Повторение ранее изученного и актуализация знаний:
Сообщение учащегося:
- Термин «показатель» для степени ввел в 1553 г. немецкий математик (сначала монах, а затем − профессор) Михаэль Штифель (1487-1567).
По-немецки показатель − Exponent, от лат. exponere: «выставлять напоказ»; exponens, exponentis − «выставляющий напоказ», «показывающий». Штифель же ввел дробные и нулевой показатели степени.
Само обозначение ax для натуральных показателей степени ввел Рене Декарт (1637 г.), а свободно обращаться с такими же дробными и отрицательными показателями стал с 1676 г. сэр Исаак Ньютон.
Степени с произвольными действительными показателями, без всякого общего определения, рассматривали и Лейбниц, и Иоганн Бернулли; в 1679 г. Лейбниц ввел понятия экспоненциальной (т.е., по-русски, показательной) функции для зависимости у=ах и экспоненциальной кривой для графика этой функции.
Краткое наименование «экспонента» отражено в одном из обозначений: ах=ахexpах. Через exp(x) обозначается конкретная экспонента − с показателем a = e = 2,71828... − встроенная во многие языки программирования функция.
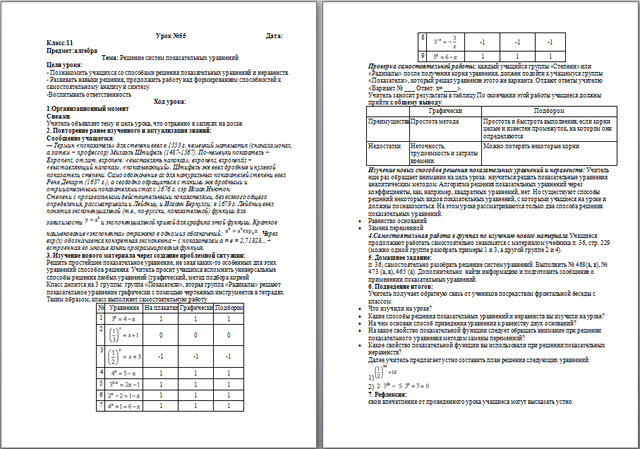
3. Изучение нового материала через создание проблемной ситуации:
Решить простейшее показательное уравнение, не зная каких-то особенных для этих уравнений способов решения.
Учитель просит учащихся вспомнить универсальные способы решения любых уравнений (графический, метод подбора корней
Класс делится на 3 группы: группа «Показатели», вторая группа «Радикалы» решают показательное уравнение графически с помощью чертежных инструментов в тетрадях.
Таким образом, класс выполняет самостоятельную работу.
Проверка самостоятельной работы: каждый учащийся группы «Степени» или «Радикалы» после получения корня уравнения, должен подойти к учащемуся группы «Показатели», который решал уравнение этого же варианта .Отдают ответы учителю «Вариант № ___ Ответ: x= ____».
Учитель заносит результаты в таблицу.По окончании этой работы учащиеся должны прийти к общему выводу.
Изучение новых способов решения показательных уравнений и неравенств: Учитель еще раз обращает внимание на цель урока: научиться решать показательные уравнения аналитическим методом.
Алгоритма решения показательных уравнений через коэффициенты, как, например, квадратных уравнений, нет.
Но существуют способы решений некоторых видов показательных уравнений, с которыми учащиеся на уроке и должны познакомиться.
На этом уроке рассматриваются только два способа решения показательных уравнений:
Равенство оснований
Замена переменной
4. Самостоятельная работа в группах по изучению нового материала.
Учащиеся продолжают работать самостоятельно знакомятся с материалом учебника п. 36, стр. 229 (можно одной группе разобрать примеры 1 и 3, а другой группе 2 и 4).
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Решение систем показательных уравнений (конспект урока) (24.04 КB)
Решение систем показательных уравнений (конспект урока) (24.04 КB)
 0
0 1133
1133 227
227 Нравится
0
Нравится
0


