Решение планиметрических задач на нахождение площадей фигур

Вашему вниманию представлены тридцать три прототипа задачи № 11 ГИА – 2013.

Три задачи - нахождение площади прямоугольника;

Три задачи - нахождение площади параллелограмма;

Три задачи - нахождение площади трапеции;

Семнадцать задач - нахождение площади треугольника (прямоугольный треугольник, равнобедренный треугольник, равносторонний треугольник, произвольный треугольник);

Три задачи - нахождение площади ромба;

Четыре задачи - нахождение площади круга и сектора;

Четыре задачи - нахождение площади любого многоугольника на клетчатой бумаге с целочисленными вершинами. (Формула Пика).

ГИА 2013

Подготовка к ГИА

Решение планиметрических

задач на нахождение

площадей фигур.

Задача №11

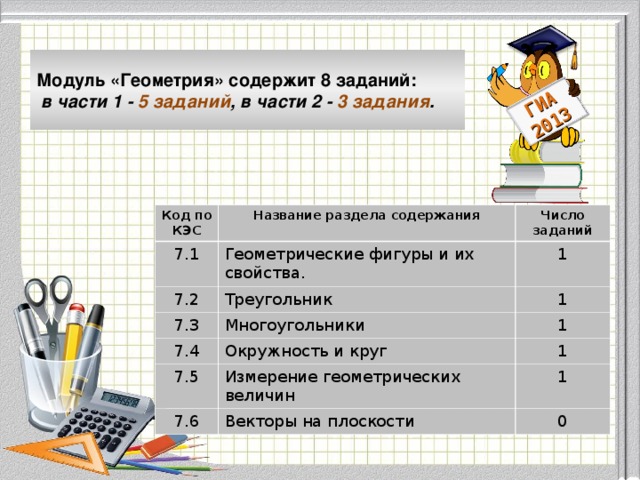
Модуль «Геометрия» содержит 8 заданий: в части 1 - 5 заданий, в час-

ти 2 - 3 задания.

МОУ «ООШ № 78» г. Саратова

Учитель: Бессонова Жанна Петровна

ГИА 2013

Модуль «Геометрия» содержит 8 заданий:

в части 1 - 5 заданий , в части 2 - 3 задания .

Код по КЭС

7.1

Название раздела содержания

Число заданий

Геометрические фигуры и их свойства.

7.2

7.3

1

Треугольник

7.4

1

Многоугольники

7.5

1

Окружность и круг

1

Измерение геометрических величин

7.6

1

Векторы на плоскости

0

Модуль «Геометрия» содержит 8 заданий: в части 1 - 5 заданий, в час-

ти 2 - 3 задания.

ГИА 2013

Код раздела

Код контролируемого элемента

7.5

Элементы содержания,

проверяемые на ГИА

7.5.1

7.5.2

Длина отрезка, длина ломаной, периметр многоугольника. Расстояние от точки до прямой

7.5.3

Длина окружности

7.5.4

Градусная мера угла, соответствие между величиной угла и длиной дуги окружности

Площадь и ее свойства. Площадь прямоугольника

7.5.5

7.5.6

Площадь параллелограмма

Площадь трапеции

7.5.7

7.5.8

Площадь треугольника

Площадь круга, площадь сектора

Модуль «Геометрия» содержит 8 заданий: в части 1 - 5 заданий, в час-

ти 2 - 3 задания.

ГИА 2013

Вашему вниманию представлены

тридцать три

прототипа задачи № 11

ГИА – 2013 .

Прямоугольник.

Параллелограмм.

Модуль «Геометрия» содержит 8 заданий: в части 1 - 5 заданий, в час-

ти 2 - 3 задания.

Трапеция.

Треугольник.

Ромб.

Круг. Круговой сектор.

Формула Пика

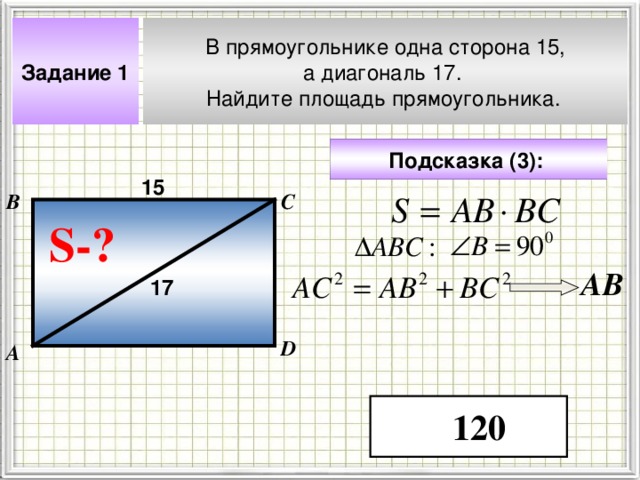
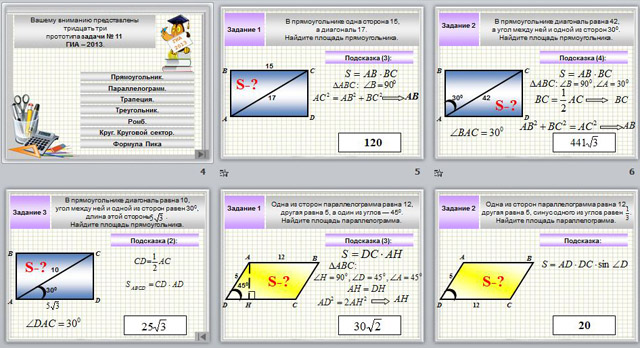
В прямоугольнике одна сторона 15,

а диагональ 17.

Найдите площадь прямоугольника.

Задание 1

Подсказка ( 3 ):

15

В

С

S- ?

A В

17

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

D

А

120

4

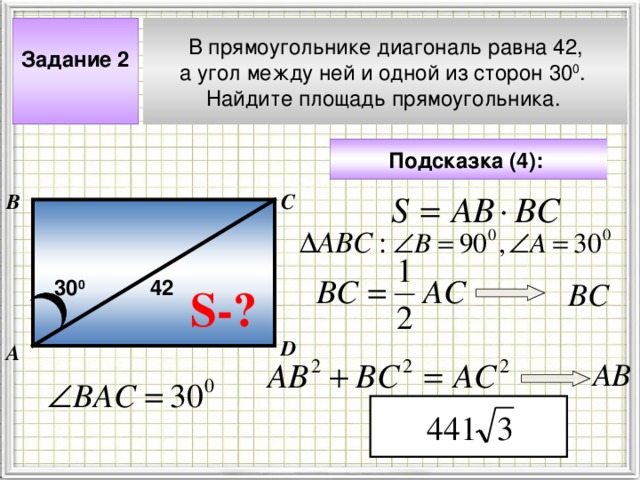
В прямоугольнике диагональ равна 42,

а угол между ней и одной из сторон 30 0 .

Найдите площадь прямоугольника.

Задание 2

Подсказка (4):

В

С

30 0

В C

42

S- ?

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

D

А

АВ

4

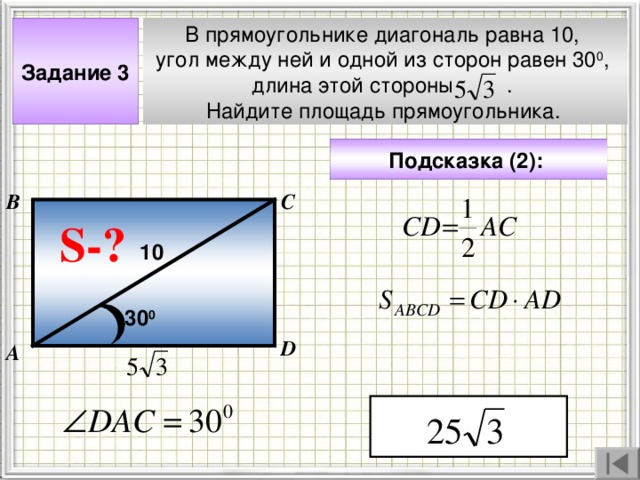
Задание 3

В прямоугольнике диагональ равна 10,

угол между ней и одной из сторон равен 30 0 ,

длина этой стороны .

Найдите площадь прямоугольника.

Подсказка (2):

В

С

S- ?

10

30 0

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

D

А

4

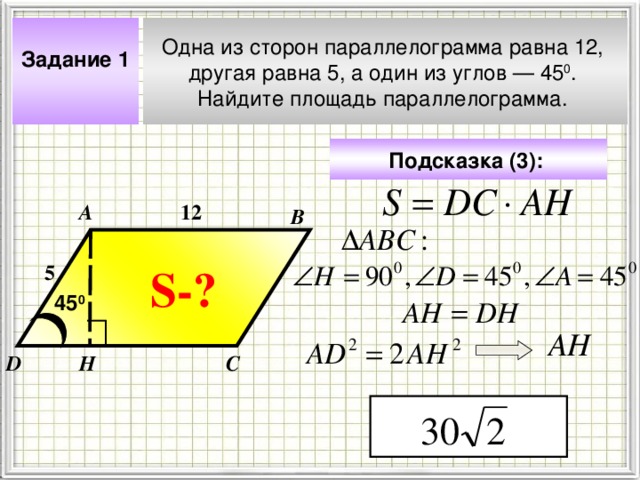
Одна из сторон параллелограмма равна 12,

другая равна 5, а один из углов — 45 0 .

Найдите площадь параллелограмма.

Задание 1

Подсказка (3):

12

А

В

S- ?

5

45 0

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

АН

Н

С

D

4

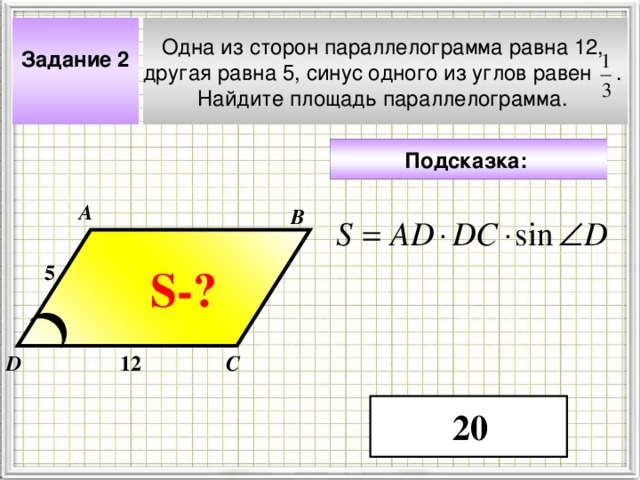
Одна из сторон параллелограмма равна 12,

другая равна 5, синус одного из углов равен .

Найдите площадь параллелограмма.

Задание 2

Подсказка:

А

В

5

S- ?

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

12

D

С

20

4

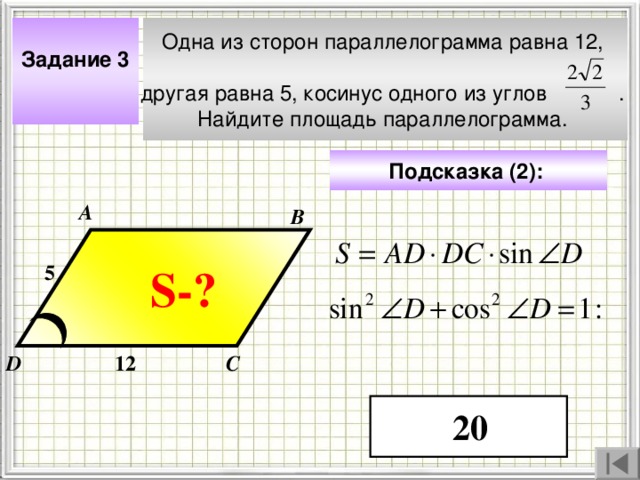
Одна из сторон параллелограмма равна 12,

другая равна 5, косинус одного из углов  .

Найдите площадь параллелограмма.

Задание 3

Подсказка (2):

А

В

5

S- ?

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

12

D

С

20

4

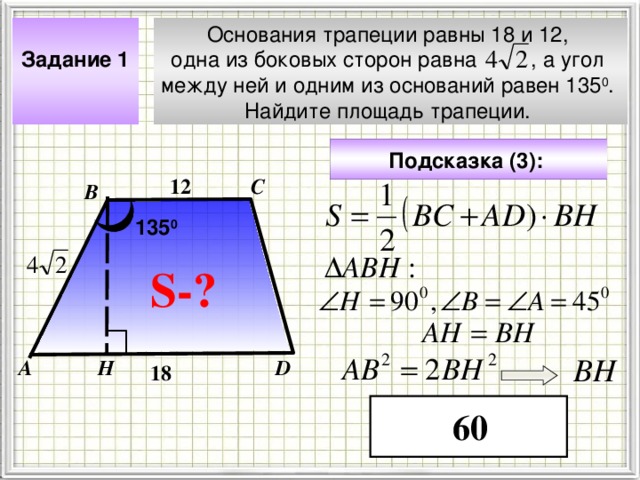
Задание 1

Основания трапеции равны 18 и 12,

одна из боковых сторон равна , а угол

между ней и одним из оснований равен 135 0 .

Найдите площадь трапеции.

Подсказка (3):

С

12

В

135 0

S- ?

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

ВН

Н

D

А

18

60

4

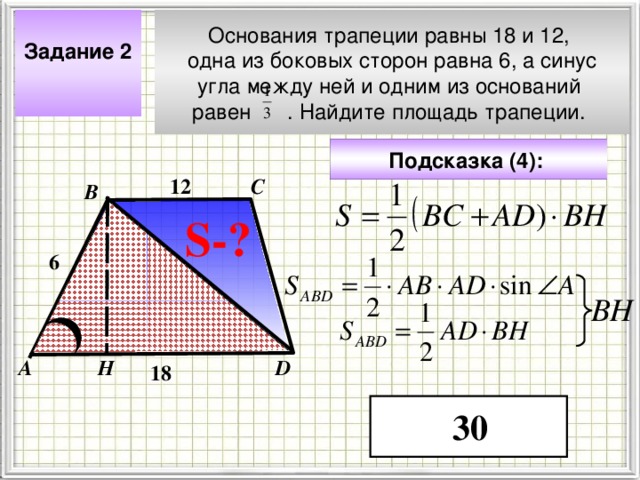
Задание 2

Основания трапеции равны 18 и 12,

одна из боковых сторон равна 6, а синус

угла между ней и одним из оснований

равен . Найдите площадь трапеции.

Подсказка (4):

С

12

В

S- ?

6

ВН

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

Н

А

D

18

30

4

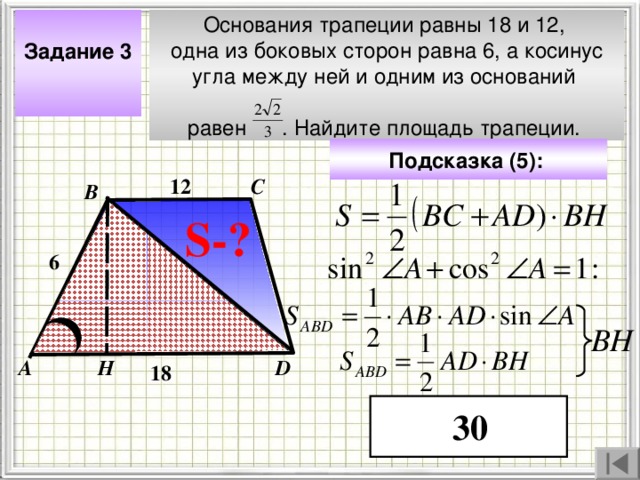
Задание 3

Основания трапеции равны 18 и 12,

одна из боковых сторон равна 6, а косинус

угла между ней и одним из оснований

равен . Найдите площадь трапеции.

Подсказка (5):

12

С

В

S- ?

6

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

ВН

Н

А

D

18

30

4

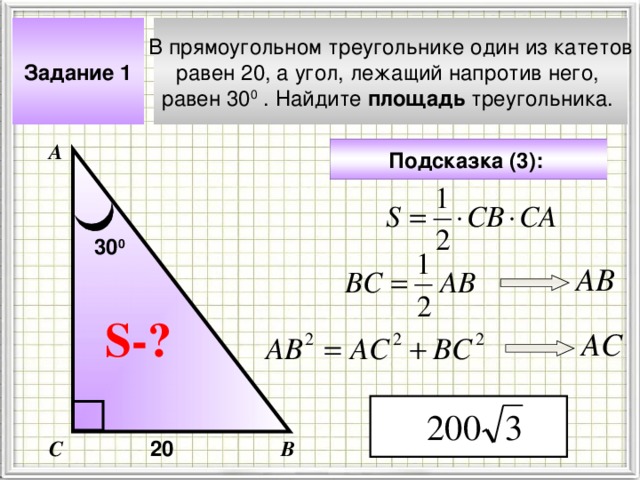
Задание 1

В прямоугольном треугольнике один из катетов

равен 20, а угол, лежащий напротив него,

равен 30 0 . Найдите площадь треугольника.

А

Подсказка (3):

30 0

АВ

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

S- ?

АС

20

С

В

4

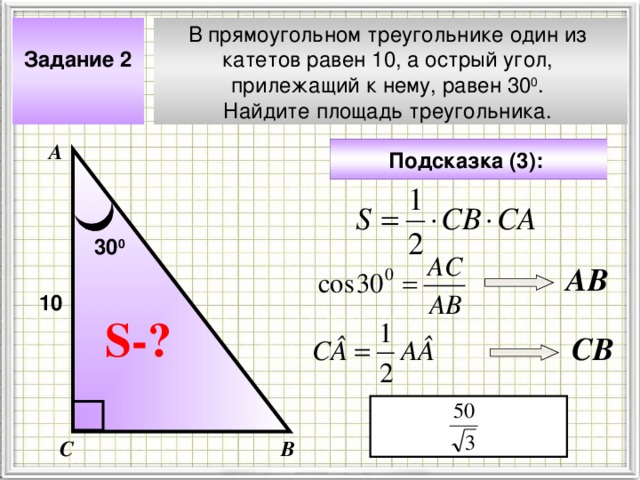
Задание 2

В прямоугольном треугольнике один из

катетов равен 10, а острый угол,

прилежащий к нему, равен 30 0 .

Найдите площадь треугольника.

А

Подсказка (3):

30 0

АВ

10

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

S- ?

CB

С

В

4

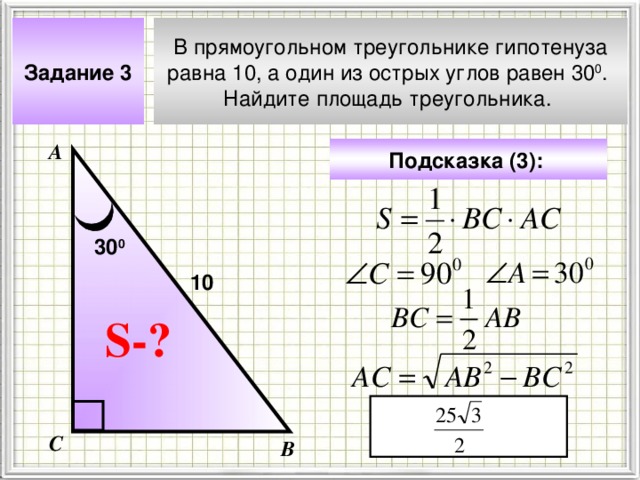
Задание 3

В прямоугольном треугольнике гипотенуза

равна 10, а один из острых углов равен 30 0 .

Найдите площадь треугольника.

А

Подсказка (3):

30 0

10

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

S- ?

С

В

4

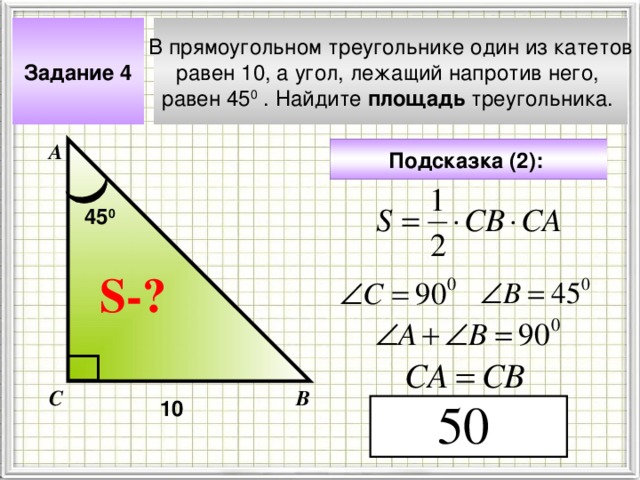
В прямоугольном треугольнике один из катетов

равен 10, а угол, лежащий напротив него,

равен 45 0 . Найдите площадь треугольника.

Задание 4

А

Подсказка (2):

45 0

S- ?

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

С

В

10

4

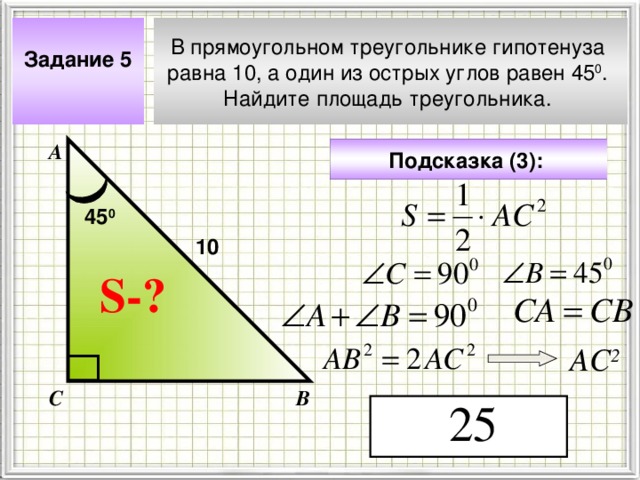
Задание 5

В прямоугольном треугольнике гипотенуза

равна 10, а один из острых углов равен 45 0 .

Найдите площадь треугольника.

А

Подсказка (3):

45 0

10

S- ?

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

АС 2

С

В

4

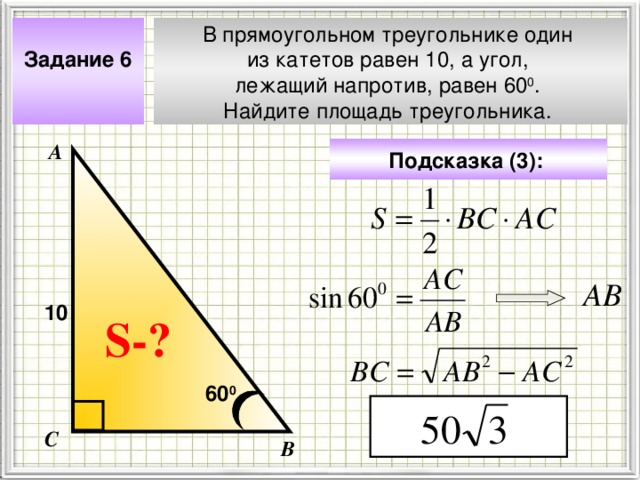
Задание 6

В прямоугольном треугольнике один

из катетов равен 10, а угол,

лежащий напротив, равен 60 0 .

Найдите площадь треугольника.

А

Подсказка (3):

АВ

10

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

S- ?

60 0

С

В

4

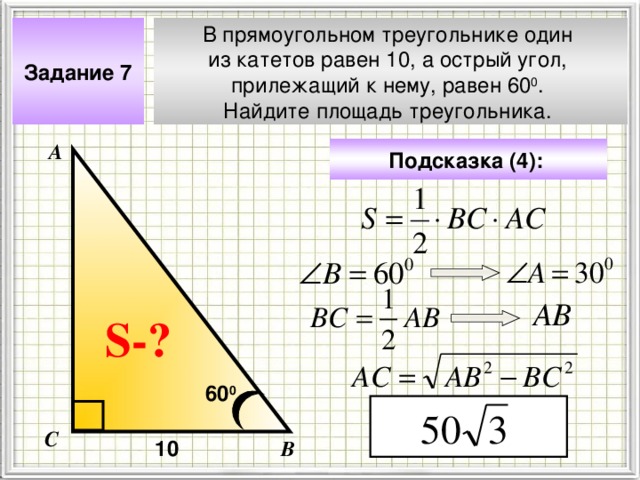
Задание 7

В прямоугольном треугольнике один

из катетов равен 10, а острый угол,

прилежащий к нему, равен 60 0 .

Найдите площадь треугольника.

А

Подсказка (4):

АВ

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

S- ?

60 0

С

10

В

4

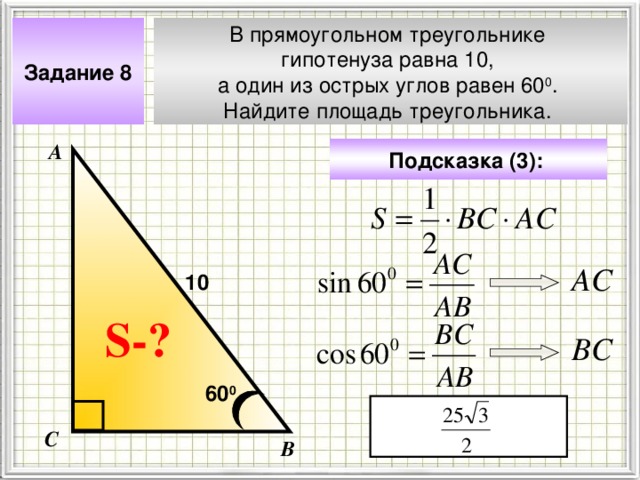
В прямоугольном треугольнике

гипотенуза равна 10,

а один из острых углов равен 60 0 .

Найдите площадь треугольника.

Задание 8

А

Подсказка (3):

АС

10

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

S- ?

ВС

60 0

С

В

4

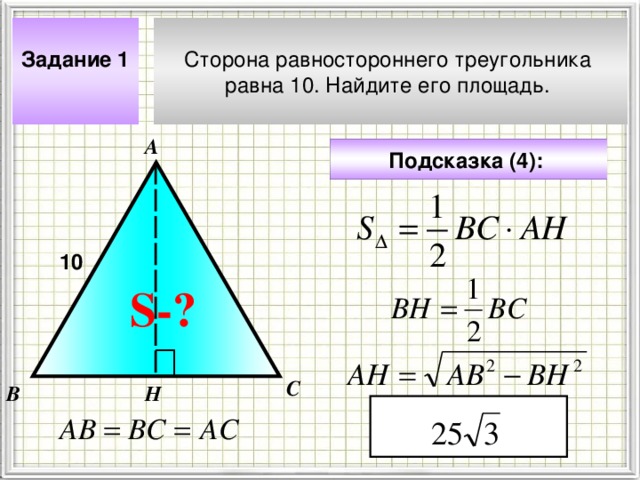
Сторона равностороннего треугольника

равна 10. Найдите его площадь.

Задание 1

А

Подсказка (4):

10

S- ?

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

С

В

Н

4

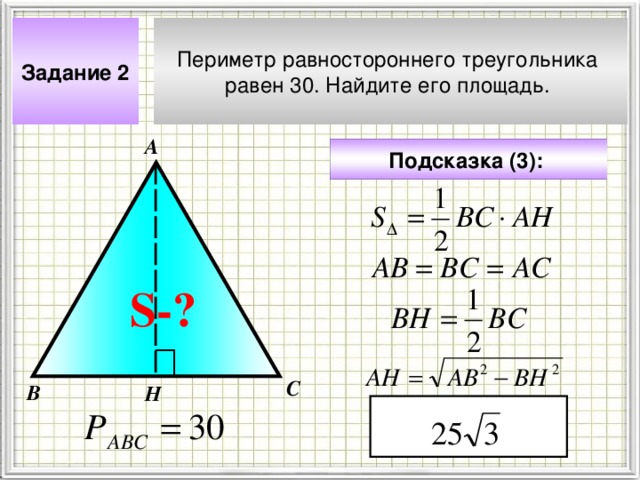
Периметр равностороннего треугольника

равен 30. Найдите его площадь.

Задание 2

А

Подсказка (3):

S- ?

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

С

В

Н

4

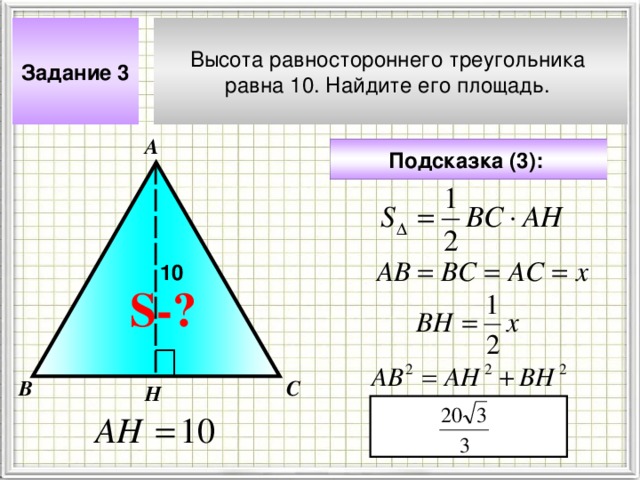
Высота равностороннего треугольника

равна 10. Найдите его площадь.

Задание 3

А

Подсказка (3):

10

S- ?

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

В

С

Н

4

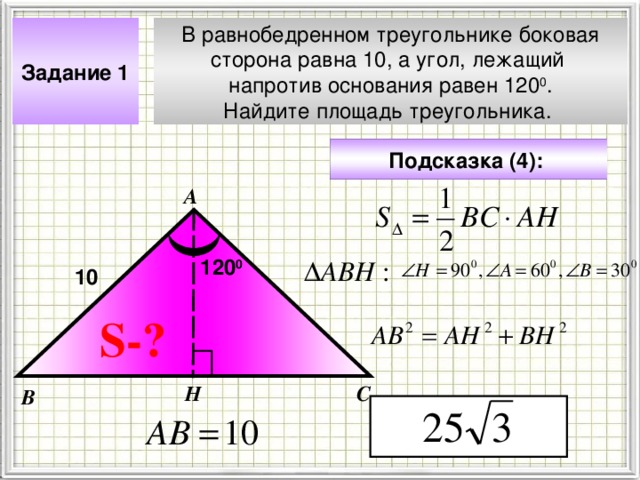
В равнобедренном треугольнике боковая

сторона равна 10, а угол, лежащий

напротив основания равен 120 0 .

Найдите площадь треугольника.

Задание 1

Подсказка (4):

А

120 0

10

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

S- ?

Н

С

В

4

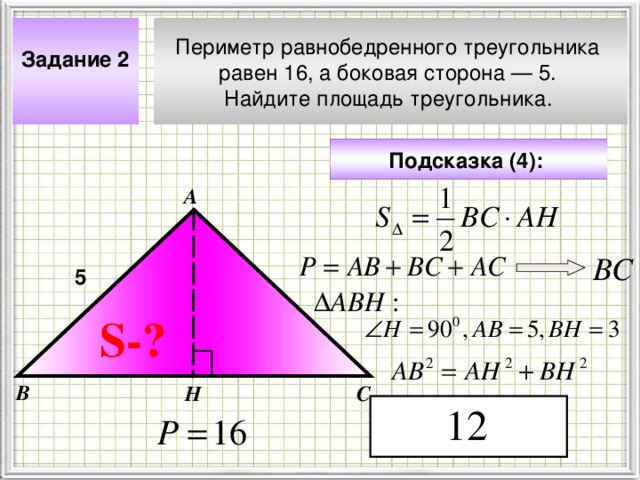
Задание 2

Периметр равнобедренного треугольника

равен 16, а боковая сторона — 5.

Найдите площадь треугольника.

Подсказка (4):

А

ВС

5

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

S- ?

В

Н

С

4

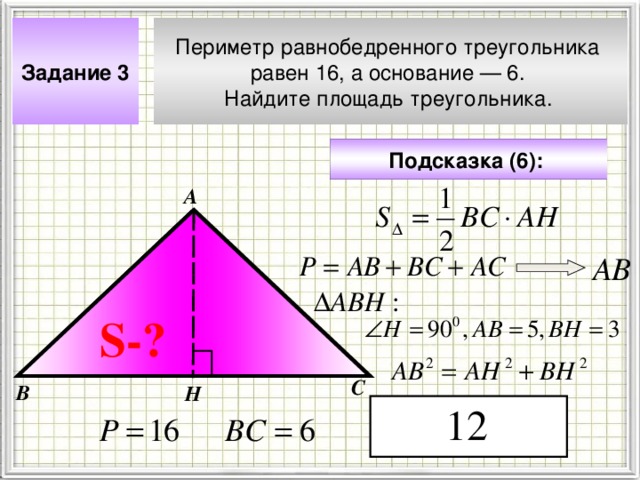
Периметр равнобедренного треугольника

равен 16, а основание — 6.

Найдите площадь треугольника.

Задание 3

Подсказка (6):

А

АВ

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

S- ?

С

В

Н

4

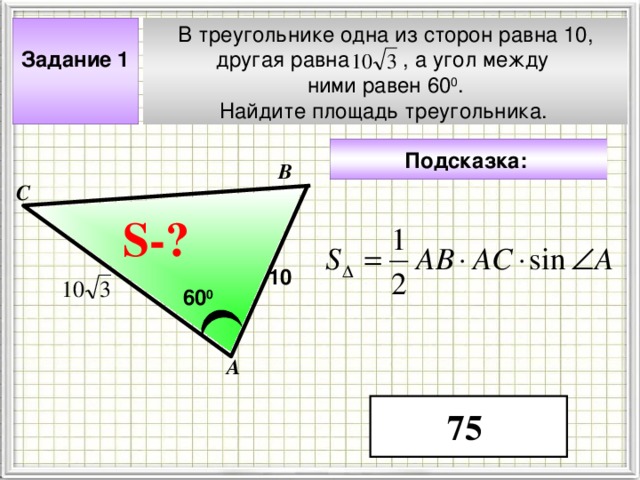
В треугольнике одна из сторон равна 10,

другая равна , а угол между

ними равен 60 0 .

Найдите площадь треугольника.

Задание 1

Подсказка:

В

С

S- ?

?

10

60 0

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

А

75

4

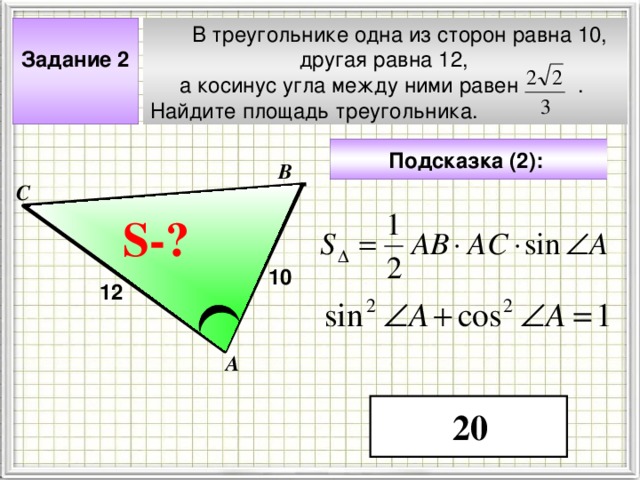
В треугольнике одна из сторон равна 10,

другая равна 12,

а косинус угла между ними равен .

Найдите площадь треугольника.

Задание 2

Подсказка (2):

В

С

S- ?

?

10

12

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

А

20

4

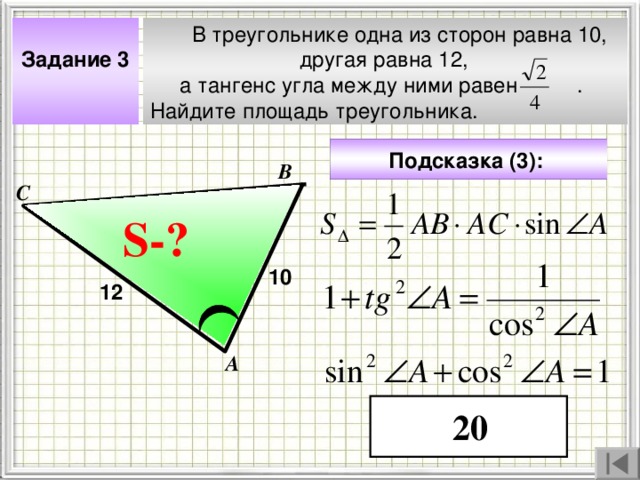
В треугольнике одна из сторон равна 10,

другая равна 12,

а тангенс угла между ними равен .

Найдите площадь треугольника.

Задание 3

Подсказка (3):

В

С

S- ?

?

10

12

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

А

20

4

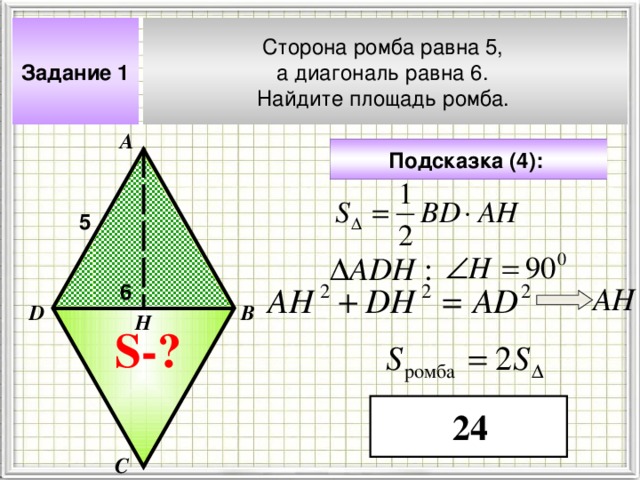
Сторона ромба равна 5,

а диагональ равна 6.

Найдите площадь ромба.

Задание 1

А

Подсказка (4):

5

6

АН

D

В

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

Н

S- ?

24

С

4

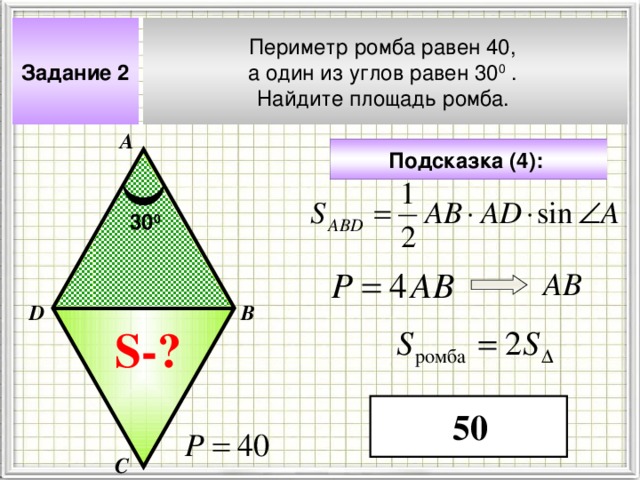
Задание 2

Периметр ромба равен 40,

а один из углов равен 30 0 .

Найдите площадь ромба.

А

Подсказка (4):

30 0

АВ

В

D

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

S- ?

50

С

4

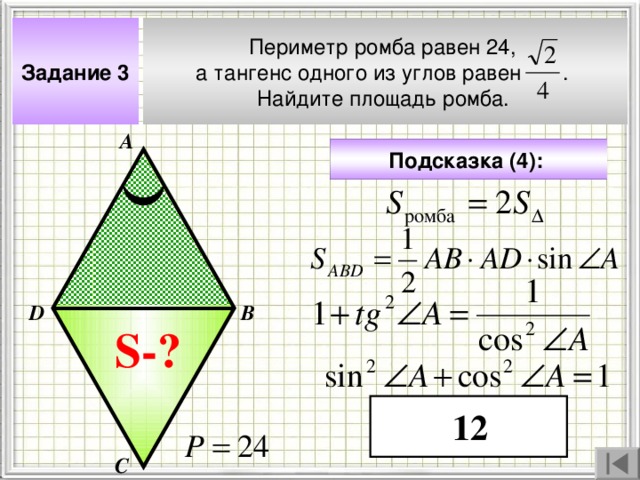
Периметр ромба равен 24,

а тангенс одного из углов равен .

Найдите площадь ромба.

Задание 3

А

Подсказка (4):

В

D

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

S- ?

12

С

4

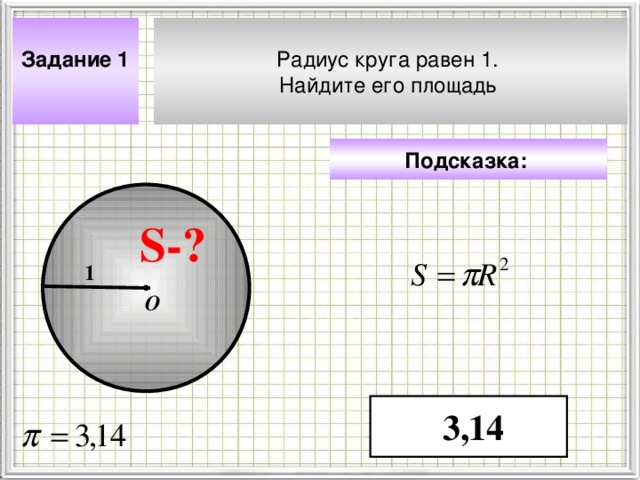
Задание 1

Радиус круга равен 1.

Найдите его площадь

Подсказка:

S- ?

1

О

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

3,14

4

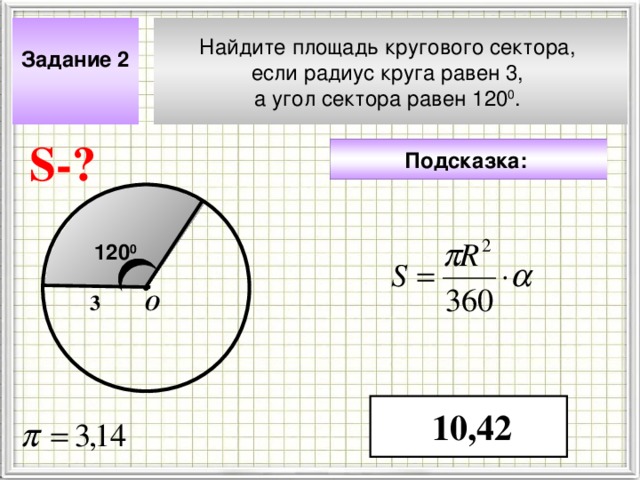
Задание 2

Найдите площадь кругового сектора,

если радиус круга равен 3,

а угол сектора равен 120 0 .

S- ?

Подсказка:

120 0

О

3

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

10,42

4

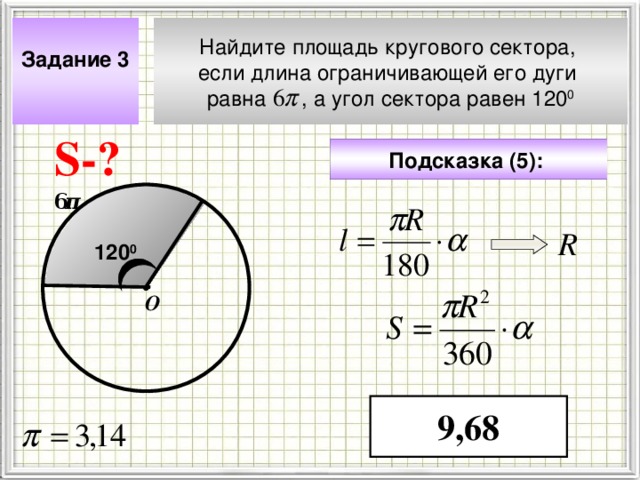
Задание 3

Найдите площадь кругового сектора,

если длина ограничивающей его дуги

равна , а угол сектора равен 120 0

S- ?

Подсказка (5):

6 π

R

120 0

О

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

9,68

4

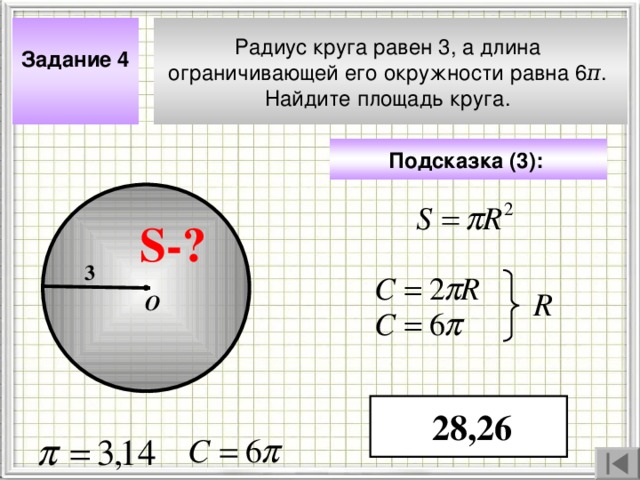
Задание 4

Радиус круга равен 3, а длина

ограничивающей его окружности равна 6 π .

Найдите площадь круга.

Подсказка (3) :

S- ?

3

R

О

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

28 , 26

4

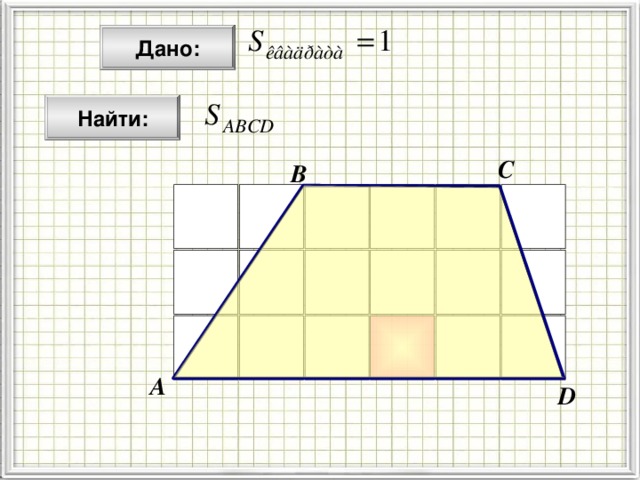
Дано:

Найти:

C

B

А

D

Формула Пика позволит вам с необычайной легкостью находить площадь любого многоугольника на клетчатой бумаге с целочисленными вершинами.

Именно такие задания предлагают на ЕГЭ в задании В3.

Площадь многоугольника с целочисленными вершинами равна

где В — количество целочисленных точек внутри многоугольника, а Г  — количество целочисленных точек на границе многоугольника.

Формула Пика очень удобна когда сложно догадаться, как разбить фигуру на удобные многоугольники или достроить…

Г

– 1

B

+

2

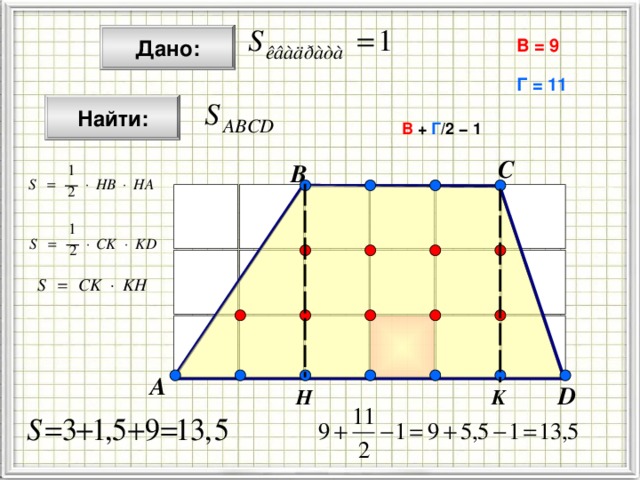
Дано:

В = 9

Г = 11

Найти:

В + Г /2 − 1

C

B

А

D

Н

K

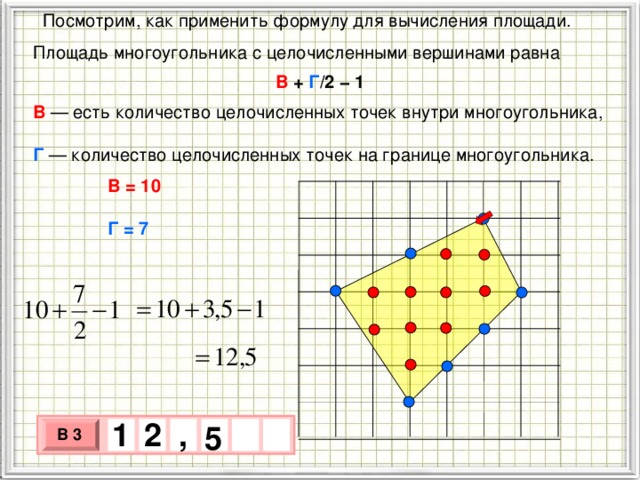
Посмотрим, как применить формулу для вычисления площади.

Площадь многоугольника с целочисленными вершинами равна

В + Г /2 − 1

В   — есть количество целочисленных точек внутри многоугольника, Г  — количество целочисленных точек на границе многоугольника.

В = 10

Г = 7

1

,

2

5

В 3

х

3

х

1

0

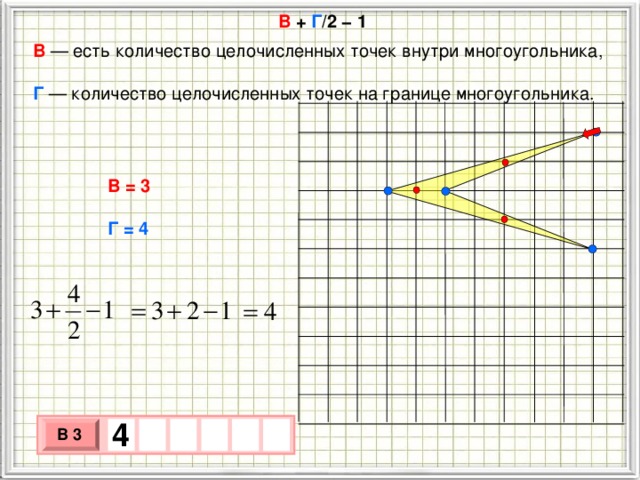
В + Г /2 − 1

В   — есть количество целочисленных точек внутри многоугольника, Г  — количество целочисленных точек на границе многоугольника.

В = 3

Г = 4

4

В 3

х

3

х

1

0

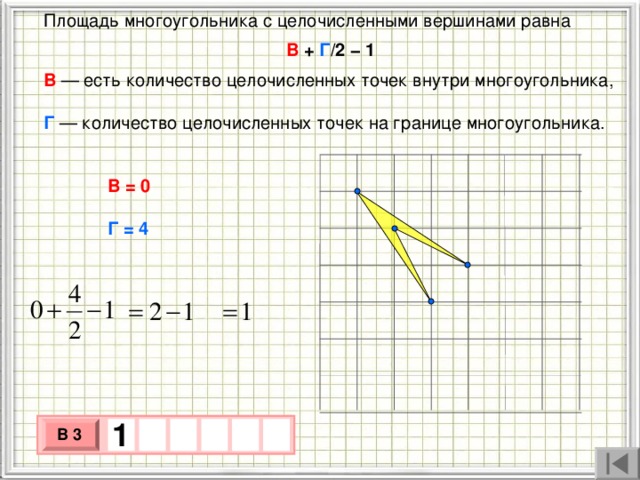
Площадь многоугольника с целочисленными вершинами равна

В + Г /2 − 1

В   — есть количество целочисленных точек внутри многоугольника, Г  — количество целочисленных точек на границе многоугольника.

В = 0

Г = 4

1

В 3

х

3

х

1

0

ГИА 2013

При создании презентации были

использованы задачи с сайта

«Открытый банк заданий по математике»

ГИА – 2012.

http://www.mathgia.ru:8080/or/gia12/Main.html;jsessionid=D398558A1FBED9E6AADAE948B798BCD1?view=Content

Клипарт «Сова» - http://radikal.ru/F/i028.radikal.ru/0710/8e/d0099ff9a62f.png.html

Модуль «Геометрия» содержит 8 заданий: в части 1 - 5 заданий, в час-

ти 2 - 3 задания.

Фон для презентации с сайта: http://pedsovet.su/

ГИА 2013

Книги по подготовке к ГИА

Модуль «Геометрия» содержит 8 заданий: в части 1 - 5 заданий, в час-

ти 2 - 3 задания.

27.12.16

45

45

ГИА 2013

1. ОТКРЫТЫЙ БАНК ЗАДАНИЙ ПО МАТЕМАТИКЕ

http://mathgia.ru/or/gia12/ShowProblems.html?posMask=8192&showProto=true

2. ФОРМУЛА ПИКА

http://www.etudes.ru/ru/etudes/pick/

3. ПОДГОТОВКА К ГИА ПО МАТЕМАТИКЕ, КНИГИ МОЖНО СКАЧАТЬ

http://4ege.ru/gia-matematika/

4. ОНЛАЙН-ТЕСТЫ ПО НОВОЙ ФОРМЕ – 2013г. (1 вариант)

http://5ballov.qip.ru/test/gia/

5. ОНЛАЙН-ТЕСТЫ 2013г.

http://uztest.ru/exam?idexam=28

6. Видео разбор демоверсии ГИА 2013 по математике

http://4ege.ru/gia-matematika/2715-video-razbor-demoversii-gia-2013-po-matematike.html

7. ОНЛАЙН-ТЕСТЫ ПО НОВОМУ ПЛАНУ ГИА в 9 вариантах

http://ege.yandex.ru/mathematics-gia/

8. Тренировочные тесты для подготовки к ГИА (2013). (Личный сайт учителя Фоновой Натальи Леонидовны)

http://madam-fonova.ucoz.ru/publ/testy_dlja_podgotovki_k_gia_po_matematike_9_klass/30-1-2

Модуль «Геометрия» содержит 8 заданий: в части 1 - 5 заданий, в час-

ти 2 - 3 задания.

ГИА 2013

Книги по подготовке к ГИА

Модуль «Геометрия» содержит 8 заданий: в части 1 - 5 заданий, в час-

ти 2 - 3 задания.