Решение квадратных уравнений (разработка урока)

Цель:

закрепление темы: «Квадратные уравнения» путем решения различных упражнений, отработки навыков решения уравнений, создавая ситуацию успеха в достижении поставленной цели. Вовлечение учащихся в атмосферу соревнования.

Содержание урока

I этап:

Класс делится на 2 команды.

Представления двух соревнующихся команд и их капитанов, состава жюри. Устанавливается количество баллов за каждый конкурс.

II этап:

команды отвечают по очереди на три вопроса.

Вопросы команде I

1 Дайте определение квадратного уравнения.

2 Какие квадратные уравнения называются неполными?

3 По какой основной формуле вычисляются корни квадратного уравнения?

Вопросы команде II

1 Дайте определение приведенного квадратного уравнения.

2 По какой формуле вычисляется дискриминант квадратного уравнения?

3 Какие дополнительные формулы вычисления корней квадратного уравнения вы знаете?

Полную информацию смотрите в файле. 

Урок учителя математики Истоминой Л. Г.

Тема урока: «Решение квадратных уравнений»

урока - игра: « Встреча в клубе серьезных математиков».

Цель:

закрепление темы: «Квадратные уравнения» путем решения различных упражнений, отработки навыков решения уравнений, создавая ситуацию успеха в достижении поставленной цели. Вовлечение учащихся в атмосферу соревнования.

Содержание урока

I этап:

Класс делится на 2 команды.

Представления двух соревнующихся команд и их капитанов, состава жюри. Устанавливается количество баллов за каждый конкурс.

II этап:

команды отвечают по очереди на три вопроса.

Вопросы команде I

1 Дайте определение квадратного уравнения.

2 Какие квадратные уравнения называются неполными?

3 По какой основной формуле вычисляются корни квадратного уравнения?

Вопросы команде II

1 Дайте определение приведенного квадратного уравнения.

2 По какой формуле вычисляется дискриминант квадратного уравнения?

3 Какие дополнительные формулы вычисления корней квадратного уравнения вы знаете?

III этап.

Конкурсы команд.

1.По одному человеку из каждой команды (эрудиты ) выполняют задания: Сократить дробь:

Команде I 5х²+3х-2 Команде II 2х²+11х-21

25х²-4 4х²-9

2.На закрытых досках по одному человеку от команды выполняют задание: решить уравнение и все о нем рассказать.

Команде I Команде II

х²+2х =0 х²- 4=0

3. Пока учащиеся у доски готовятся, вызывается по одному человеку из оставшихся в команде, выполняют устно задания: закончить предложение, чтобы оно было верным.

Команде I: а) Если Д

квадратного уравнения….

Команда II а) Если Д 0, то …, б) Если второй коэффициент квадратного уравнения –

четное число, то …, в) Произведение корней приведенного квадратного

уравнения … .

4. Члены команд на листочках выполняются задание по вариантам.

В – I

1) 2х² – 7х=0;

2) – 2х²- х =12;

3) х (х+3)=0;

4) х²= 4;

5) 5+х²=х;

7) 2х-4=0.

В - II

6) 5х²–16х+3=0;

3) 2х²-8=0;

1) 49=14х+2х²;

2) х²- 4х=5;

6) 35х²+2х-1=0

7) х-5=0

4) (х - 2)* х =0;

5) х²- 9=0;

а) Среди данных уравнений укажите номера тех, которые являются полными,

приведенными, неполными.

б) В уравнении №5 запишите значение коэффициентов: а, в, с.

в) Найдите сумму и произведение корней уравнения №5

г) Решите уравнение №6.

Работы сдаются в жюри, которое подводит итоги после заслушивания результатов выполнение конкурсов 1 – 3.

5. По одному человеку из команды решают на доске уравнение:

Команде I Команде II

(х+1)²+(1+х)*5=14 (х-4) (х+4)= - 2х +64

6 Одновременно с выполнением задания 5 проводится эстафета « Цепочка»: двоим учащимся, сидящим за одной партой, решить первое из записанных на карточке уравнений и передать ее следующей парте.

Уравнение для этой «цепочке»:

1. 9х²-1=0;

2. х²+2х=4;

3. х²-10х+25=0;

4. (х+1)²=9;

5. 18+3х²-х=9;

6. х²+2х-80=0;

7. – х²+3х= -5;

8. (х+1)²-1=0;

9. х²+2х-3=0;

10. 2х²+3х-5=0;

11. 6х²+х-1=0;

12. 2х²-7х+3=0;

13. 4х²-9=0;

14. х² +6х+5=0.

Команда, закончившая эстафету раньше, может решить дополнительное уравнение

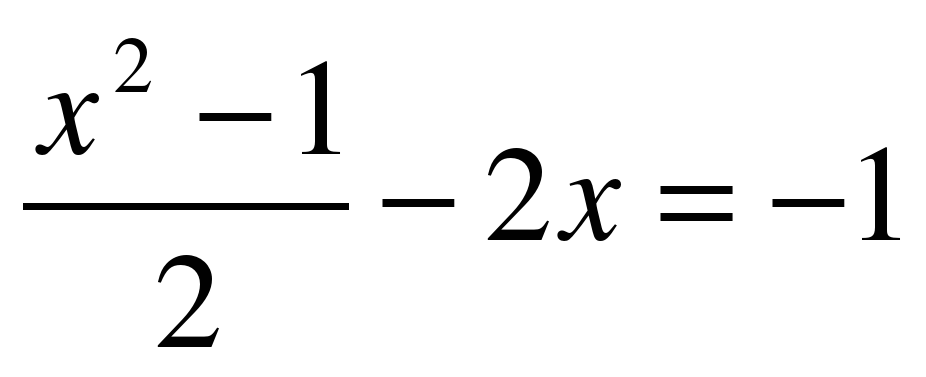и получить дополнительные баллы. После этого проверяется выполнение четвертого конкурса и домашнее задание.

7. Домашнее задание представляется под девизом:

« Кто хочет ограничиться настоящим

без знания прошлого,

тот никогда его не поймет»

Лейбниц.

Команда I Команда II

сообщение на тему сообщение на тему

«История развития учения о квадратных «Франсуа Виет»

Уравнениях».

8. Конкурс капитанов (под музыку)

1) Составить квадратное уравнение по его корням 2 и 7.

2) Найдите q, если разность корней уравнения х²-12+q=0 равна 8

9. Игра “Кто быстрее сядет в ракету” ( кто быстрее выполнит четыре задания)

Задание команде I : Задание команде II

1 Решить уравнения : 1 Решите уравнение:

1) х²=12-11х 1) х²= - 2х+48

2) х²-16х+64=0 2) х²+8х+64=0

3) Уравнение х²+6х+24=0 имеет 3) Уравнение х²-7х+с=0 имеет

корень х=8. корень х=5.

Найти в и второй корень. Найти С и второй корень.

Когда команда выполнит задание 1, один ученик идет к доске и показывает решение, затем ответ записывает на первой ступеньке ракеты. Аналогично поступают с заданиями 2,3,4, затем суммируют ответы у команды первой, получилось -11 , а у второй 10, то им выдается карточка с надписью “ взлет”, если же сумма составляет другое число, то команда считается проигравшей.

Заслушиваются результаты выполнения этого задания(9).

IV этап

Пока жюри подводит итоги, выполняются задание из рубрики «Это интересно»

1. Теорема: если в квадратном уравнении ах²+вх+с=0 сумма коэффициентов а+в+с=0, то х₁=1, х₂=

Например, в уравнении 5х²-7х+2=0 значение выражения, а +в+с=5-7+2=0, следовательно, х₁=1, х₂=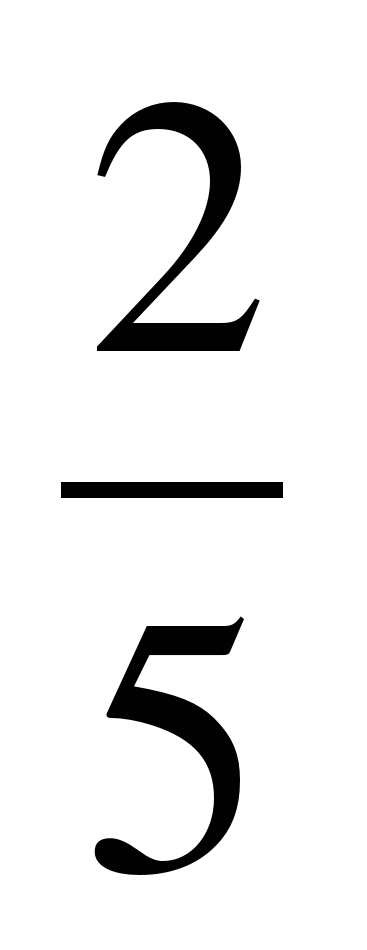

2. Теорема: если в том же уравнении а-в+с=0, то х₁= -1, х₂=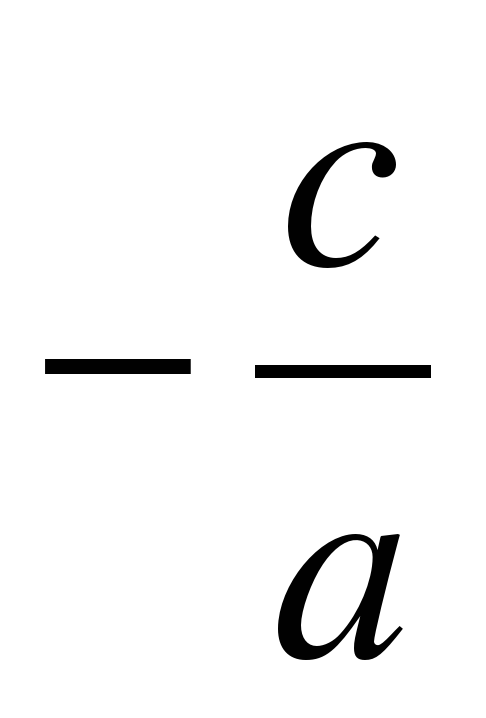

Например, в уравнении 3х²+2х-1=0 значение выражения а-в+с=3-2+(-1)=0, следовательно, х₁= - 1, х₂=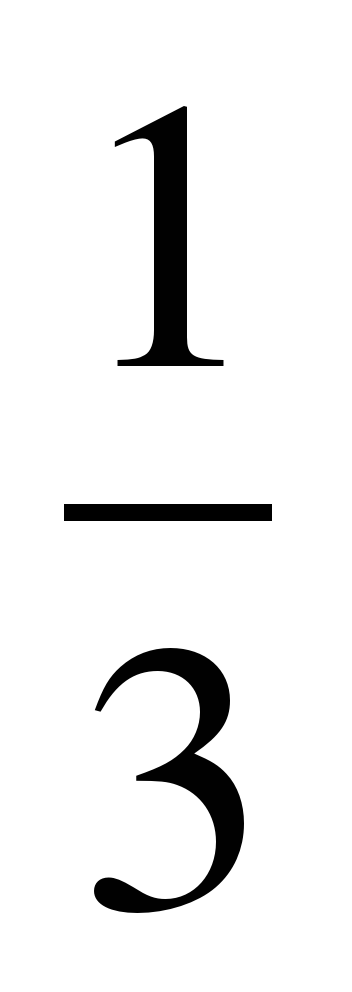

Используя теоремы, найти корни уравнения 1978х²+1984х+6=0 (х₁= -1, х₂=)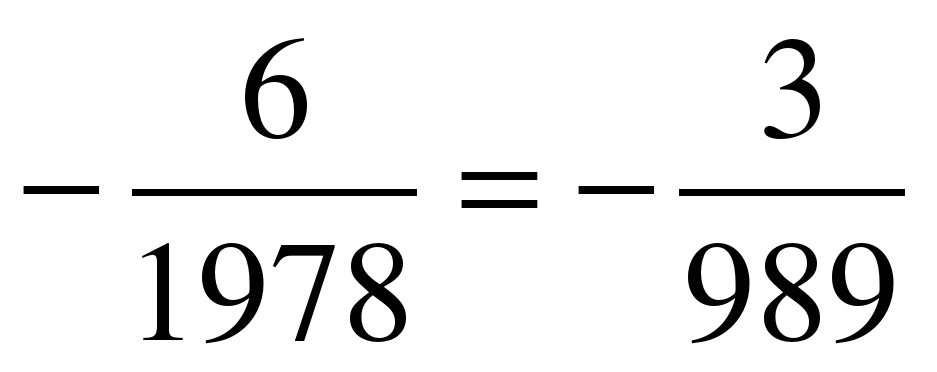

Жюри подводит общие итоги и поздравляет победителей.